
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пряма та двоїста задачі лінійного програмування
|
|
|
|
Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач
Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею. Економічну інтерпретацію кожної з пари таких задач розглянемо на прикладі виробничої задачі.
Пряма задача:
Z = c1x1 + c2x2 + … + cnxn → max (4.1)
за умов:
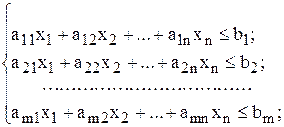 (4.2)
(4.2)
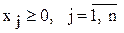 . (4.3)
. (4.3)
Необхідно визначити, яку кількість продукції кожного j- го виду 
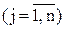 необхідно виготовляти в процесі виробництва, щоб максимізувати загальну виручку від реалізації продукції підприємства. Причому відомі: наявні обсяги ресурсів —
необхідно виготовляти в процесі виробництва, щоб максимізувати загальну виручку від реалізації продукції підприємства. Причому відомі: наявні обсяги ресурсів — 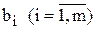 ; норми витрат і- го виду ресурсу на виробництво одиниці j- го виду продукції —
; норми витрат і- го виду ресурсу на виробництво одиниці j- го виду продукції —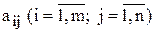 , а також
, а також 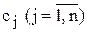 — ціни реалізації одиниці j-ої продукції.
— ціни реалізації одиниці j-ої продукції.
Розглянемо тепер цю саму задачу з іншого погляду. Допустимо, що за певних умов доцільно продавати деяку частину чи всі наявні ресурси. Необхідно визначити ціни ресурсів. Кожному ресурсу 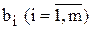 поставимо у відповідність його оцінку
поставимо у відповідність його оцінку 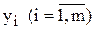 . Умовно вважатимемо, що
. Умовно вважатимемо, що 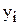 — ціна одиниці і- го ресурсу.
— ціна одиниці і- го ресурсу.
На виготовлення одиниці j- го виду продукції витрачається згідно з моделлю (4.1)—(4.3) m видів ресурсів у кількості відповідно 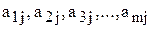 . Оскільки ціна одиниці і- го виду ресурсу дорівнює
. Оскільки ціна одиниці і- го виду ресурсу дорівнює 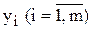 , то загальна вартість ресурсів, що витрачаються на виробництво одиниці j- го виду продукції, обчислюється у такий спосіб:
, то загальна вартість ресурсів, що витрачаються на виробництво одиниці j- го виду продукції, обчислюється у такий спосіб:
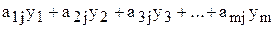 .
.
Продавати ресурси доцільно лише за умови, що виручка, отримана від продажу ресурсів, перевищує суму, яку можна було б отримати від реалізації продукції, виготовленої з тих самих обсягів ресурсів, тобто:
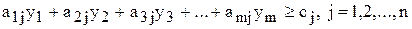 .
.
Зрозуміло, що покупці ресурсів прагнуть здійснити операцію якнайдешевше, отже, необхідно визначити мінімальні ціни одиниць кожного виду ресурсів, за яких їх продаж є доцільнішим, ніж виготовлення продукції. Загальну вартість ресурсів можна виразити формулою:
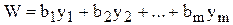 .
.
Отже, в результаті маємо двоїсту задачу:
 (4.4)
(4.4)
за умов: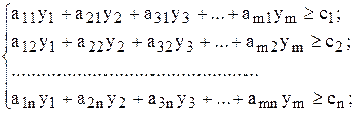 (4.5)
(4.5)
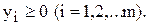 (4.6)
(4.6)
Тобто необхідно визначити, які мінімальні ціни можна встановити для одиниці кожного і- го виду ресурсу 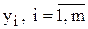 , щоб продаж ресурсів був доцільнішим, ніж виробництво продукції.
, щоб продаж ресурсів був доцільнішим, ніж виробництво продукції.
Зауважимо, що справжній зміст величин 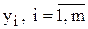 — умовні ціни, що виражають рівень «цінності» відповідного ресурсу для даного виробництва. Англійський термін «shadow prices» у літературі перекладають як «оцінка» або «тіньова, неявна ціна». Академік Л. В. Канторович назвав їх об’єктивно обумовленими оцінками відповідного ресурсу.
— умовні ціни, що виражають рівень «цінності» відповідного ресурсу для даного виробництва. Англійський термін «shadow prices» у літературі перекладають як «оцінка» або «тіньова, неявна ціна». Академік Л. В. Канторович назвав їх об’єктивно обумовленими оцінками відповідного ресурсу.
Задача (4.4)—(4.6) є двоїстою або спряженою до задачі (4.1)—(4.3), яку називають прямою (основною, початковою). Поняття двоїстості є взаємним. По суті мова йде про одну і ту ж задачу, але з різних поглядів. Дійсно, не важко переконатися, що двоїста задача до (4.4)—(4.6) збігається з початковою. Тому кожну з них можна вважати прямою, а іншу — двоїстою. Симетричність двох таких задач очевидна. Як у прямій, так і у двоїстій задачі використовують один набір початкових даних: 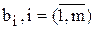 ,
, 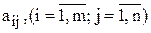 ;
; 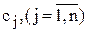 . Крім того, вектор обмежень початкової задачі стає вектором коефіцієнтів цільової функції двоїстої задачі і навпаки, а рядки матриці А (матриці коефіцієнтів при змінних з обмежень прямої задачі) стають стовпцями матриці коефіцієнтів при змінних в обмеженнях двоїстої задачі. Кожному обмеженню початкової задачі відповідає змінна двоїстої і навпаки.
. Крім того, вектор обмежень початкової задачі стає вектором коефіцієнтів цільової функції двоїстої задачі і навпаки, а рядки матриці А (матриці коефіцієнтів при змінних з обмежень прямої задачі) стають стовпцями матриці коефіцієнтів при змінних в обмеженнях двоїстої задачі. Кожному обмеженню початкової задачі відповідає змінна двоїстої і навпаки.
Початкова постановка задачі та математична модель може мати вигляд як (4.1)—(4.3), так і (4.4)—(4.6). Отже, як правило, кажуть про пару спряжених задач лінійного програмування.
3.2. Правила побудови двоїстих задач
Побудова двоїстої задачі до основної здійснюється в послідовності:
І. Стандартизація основної задачі:
1) у всіх обмеженнях вільні члени розміщені в правій частині рівності (нерівності), а члени з невідомим – у лівій;
2) усі обмеження нерівності основної задачі мають бути записані так, щоб знаки нерівності у них були спрямовані в один і той самий бік, для цього достатньо окремі нерівності помножити на (-1);
3) загальний знак нерівності системи обмежень пов’язується з оптимізацією форми таким чином: якщо max, то 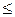 , якщо min то
, якщо min то 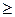 .
.
Після стандартизації основної задачі виконується послідовність, спрямованих на формування задачі обмежень (пункт ІІ) та цільової функції (пункт ІІІ) двоїстої задачі.
ІІ. При побудові системи обмежень двоїстої задачі слід дотримуватися таких правил:
1) кожному обмеженню вихідної задачі відповідає невідома уі в двоїстій задачі, причому двоїста невідома, що відповідає обмеженню нерівності має бути невід’ємною, а рівності можуть мати будь-який знак. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі;
2) кожній невідомій хі вихідної задачі відповідає обмеження двоїстої, причому кількість обмежень двоїстої задачі дорівнює кількості невідомих прямої задачі. Ці обмеження будують так: множать коефіцієнти aij, що стоять при хі, на відповідні двоїсті невідомі уі, результати множення додають і ставлять у ліву частину обмежень, а в праву – коефіцієнт при хі в оптимізуючій формі сі;
3) у всіх обмеженнях двоїстої задачі ставлять один і той же знак нерівності, протилежний загальному знаку нерівності системи обмежень вихідної задачі;
4) Матриця
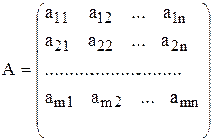 ,
,
що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі обмежень двоїстої задачі
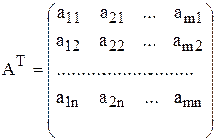
утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків — рядками.
ІІІ. Для оптимізуючої форми двоїстої задачі мають задовольнятися умови:
1) форма w двоїстої задачі оптимізується у протилежному значенні (якщо z(max), то w(min), і навпаки);
2) коефіцієнтами при двоїстих невідомих у формі W є відповідні вільні члени системи обмежень вихідної задачі. Вільний член с0 форми z переноситься без змін у форму W.
Багато задач лінійного програмування ставляться у вигляді основної або двоїстої задачі, тому є сенс говорити про пару двоїстих задач лінійного програмування.
Якщо одна з пари двоїстих задач має розв’язок (тобто оптимальний план), то і друга – обов’язково має розв’язок, причому
max z = min w. (4.7)
Для побудови двоїстої задачі необхідно основну задачу звести до стандартного вигляду, враховуючи тип екстремуму цільової функції.
Оптимальне значення кожної змінної двоїстої задачі визначає позитивний або негативний приріст значення цільової функції за рахунок одиничного приросту (позитивного чи негативного) значення константи в правій частині відповідного обмеження. Оптимальні значення змінних двоїстої задачі називають прихованими доходами або тіньовими цінами. Якщо константи в правих частинах обмежень задають обсяги наявних ресурсів, приховані доходи визначають внесок у прибуток, отриманий за рахунок одиниці кожного з ресурсів, відповідно до виду оптимального рішення прямої задачі.
Коефіцієнти aij інтерпретуються як відповідні норми споживання і-го ресурсу в j-му виробничому процесі. Сумою 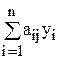 задається економічний ефект за рахунок j-го виробничо-технологічного процесу, обчислений з урахуванням прихованого доходу.
задається економічний ефект за рахунок j-го виробничо-технологічного процесу, обчислений з урахуванням прихованого доходу.
Пари задач лінійного програмування бувають симетричні та несиметричні.
У симетричних задачах обмеження прямої та двоїстої задач є лише нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень.
У несиметричних задачах деякі обмеження прямої задачі можуть бути рівняннями, а двоїстої — лише нерівностями. У цьому разі відповідні рівнянням змінні двоїстої задачі можуть набувати будь-яких значень, не обмежених знаком.
Всі можливі форми прямих задач лінійного програмування та відповідні їм варіанти моделей двоїстих задач у матричній формі наведено нижче.
| Пряма задача | Двоїста задача |
| Cиметричні задачі | |
Z = CX → max
AX 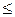 B
X B
X 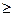 0 0
| W = B → min
ATY 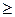 C
Y C
Y 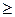 0 0
|
Z = CX → min
AX 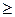 B
X B
X 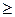 0 0
| W = BY → max
ATY 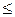 C
Y C
Y 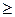 0 0
|
Несиметричні задачі
Z = CX → max
AX = B
X 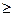 0 0
| W = B → min
ATY 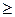 C
Y C
Y 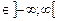
|
Z = CX → min
AX = B
X 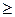 0 0
| W = BY → max
ATY 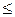 C
Y C
Y 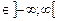
|
Теорія двоїстості є потужним математичним апаратом обґрунтування структури виробництва. Вона дає змогу насамперед визначати статус ресурсів та інтервали стійкості двоїстих оцінок відносно зміни запасів дефіцитних ресурсів. За умов ринкової економіки ціни на ресурси можуть змінюватися в доволі широких межах. Крім цього, постачальники через об’єктивні обставини можуть не виконати попередніх домовленостей. Тому аналіз ринку ресурсів у передплановому періоді має чимале значення.
Використання двоїстих оцінок уможливлює визначення рентабельності кожного виду продукції, яка виробляється підприємством. Водночас можна оцінити інтервали можливої зміни цін одиниці кожного виду продукції, що дуже важливо за ринкових умов.
Для аналізу стійкості важливим є діапазони зміни параметрів, в яких оптимальне рішення залишається оптимальним. У процесі пошуку оптимального рішення можна отримати так званий звіт про стійкість, у якому містяться межі коефіцієнтів цільової функції. Зміна коефіцієнтів в цих межах не призводить до зміни оптимального рішення. Аналогічні інтервали встановлюються для запасів ресурсів. При виході за визначені межі стійкості оптимальне рішення може мінятися як за номенклатурою продукції, що випускається, так і за обсягами випуску (без зміни номенклатури).
Отже, аналіз лінійної економіко-математичної моделі на чутливість дає широкий спектр динамічної інформації про визначений оптимальний план і змогу дослідити вплив можливих змін на результати господарської діяльності.
Побудована економіко-математична модель може бути використана для імітації процесу виробництва. Це дає змогу перевірити:
1) за яких умов оптимальний план є стійким;
2) чи є вигідним додаткове залучення ресурсів;
3) як зміниться ефективність виробництва в разі загострення конкуренції на ринку збуту (оцінити виправданість у цій ситуації зниження цін на продукцію);
4) доцільність виробництва нової продукції;
5) як вплине на ефективність діяльності підприємства порушення споживачами продукції попередніх угод, наприклад, їх відмова від частини або всієї продукції. Як має виробник за цих обставин змінити план виробництвом продукції, щоб уникнути втрат, пов’язаних із надвиробництвом відповідного виду продукції.
Зауважимо, що дослідження планів, отриманих за економіко-математичними моделями, на стійкість, а також оцінювання ситуацій мають виконуватися в передплановому періоді.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 4442; Нарушение авторских прав?; Мы поможем в написании вашей работы!