Кван­товые числа. Атомные орбитали

Волновую функцию (7), описывающую состояние электрона, называют атомной орбиталью (АО).

Квантовые числа. В квантовой механике каждая АО определяется тремя квантовыми числами.

Главное квантовое число n. Может принимать целочисленные значения от 1 до ∞. Главное квантовое число определяет:

номер энергетического уровня;

интервал энергий электронов, находящихся на данном уровне;

размеры орбиталей;

число подуровней данного энергетического уровня (первый уровень состоит из одного подуровня, второй – из двух, третий – из трех и т.д.);

В Периодической системе элементов максимальному значению главного квантового числа соответствует номер периода.

Орбитальное квантовое число l. Определяет орбитальный момент количества движения (импульс) электрона, точное значение его энергии и форму орбиталей. Может принимать значения 0, 1, 2, 3, …, (n -1).

Атомная орбиталь – геометрический образ одноэлектронной волновой функции ψ, представляющий собой область наиболее вероятного пребывания электрона в атоме. Она ограничивает область пространства, в которой вероятность нахождения электрона имеет определенное значение (90 …99 %). Иногда орбиталью называют граничную поверхность этой области, а на рисунках, как правило, изображают сечение этой области плоскостью, проходящей через начало координат и лежащей в плоскости рисунка. В начало координат помещают центр ядра атома. Понятие «орбиталь», в отличие от «орбита», не подразумевает знания точных координат электрона. Орбитальное квантовое число определяет форму атомной орбитали. При l =0 это сфера, при l =1 – объемная восьмерка (гантель), при l =2 – четырехлепестковая розетка.

Каждому значению главного квантового числа соответствует n значений орбитального квантового числа l (табл. 1). Например, если n =1, то l принимает только одно значение (l =0), n =2 – два значения: 0 и 1 и т.д. Каждому численному значению l соответствует определенная геометрическая форма орбиталей и приписывается буквенное обозначение. Первые четыре буквы обозначения имеют историческое происхождение и связаны с характером спектральных линий. s, p, d, f – первые буквы английских слов, использованных для названия спектральных линий: sharp (резкий), principal (главный), diffuse (диффузный), fundamental (основной). Обозначения других орбиталей приведены в алфавитном порядке: g, h, …

Таблица 1

Значения главного и орбитального квантовых чисел

Орбитальное квантовое число l

Главное квантовое число n

Значение Буквенное обозначение

s

s

p

s

p

d

s

p

d

f

s

p

d

f

g

Обозначение любого подуровня определяется двумя квантовыми числами – главным (при записи указывается численное значение) и орбитальным (при записи указывается буквенное обозначениеорбитальным ()ается численное значение двумя квантовыми числами - главным). Например, энергетический подуровень, для которого n =2 и l =1, следует обозначить так: 2р -подуровень. Все орбитали с одинаковым значением l имеют одинаковую геометрическую формулу и в зависимости от значений главного квантового числа различаются размерами. Например, все орбитали, для которых l =0 (s -орбитали) являются сферически симметричными, различаются размерами в зависимости от значения главного квантового числа. Чем выше значение n, тем больше размеры орбиталей.

Магнитное квантовое число m_l. Определяет возможные значения проекции орбитального момента количества движения электрона на фиксированное направление в пространстве (например, на ось z). Оно принимает отрицательные и положительные значения l, включая нуль. Общее число значений равно 2 l +1:

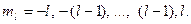
От значения магнитного квантового числа зависит взаимодействие магнитного поля, создаваемого электроном, с внешним магнитным полем. Если нет внешнего магнитного поля, то энергия электрона в атоме не зависит от m_l. В этом случае электроны с одинаковыми значениями n и l, но с разными значениями m_l обладают одинаковой энергией. Если существует внешнее магнитное поле – энергия электронов с разными m_l различается.

В общем случае магнитное квантовое число характеризует ориентацию АО в пространстве относительно внешней силы. Магнитное квантовое число определяет ориентацию орбитального углового момента относительно некоторого фиксированного направления.

Общее число возможных значений m_l соответствует числу способов расположения орбиталей данного подуровня в пространстве, то есть общему числу орбиталей на данном подуровне (табл. 2).

Таблица 2

Число орбиталей на подуровне

Главное квантовое число n	Число значений ml	Квантовое число
l	ml
		0 (s)   0 (s) 1 (p)   0 (s) 1 (p) 2 (d)	-1, 0, +1   -1, 0, +1 -2, -1, 0, +1, +2

Орбитальному квантовому числу l =0 отвечает единственное значение магнитного квантового числа m_l =0. Эти значения l и m_l характеризуют все s -орбитали, которые имеют форму сферы. Так как в этом случае магнитное квантовое число принимает только одно значение, то каждый s-подуровень состоит только из одной орбитали. Рассмотрим любой р -подуровень. При l =1 орбитали имеют форму гантелей (объемные восьмерки), магнитное квантовое число принимает следующие значения: m_l = -1, 0, +1. Следовательно, р -подуровень состоит из трех АО, которые располагаются вдоль осей координат, их обозначают p_x, p_y, p_z соответственно (рис. 1).

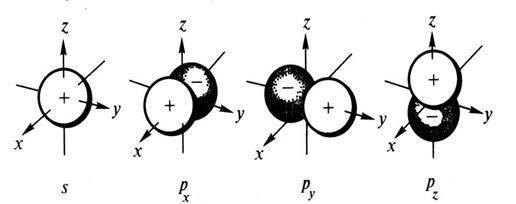
Рис. 1. Пространственная форма s- и р-атомных орбиталей.

Для d -подуровня l =2, m_l = -2, -1, 0, +1, +2 (всего 5 значений), и любой d -подуровень состоит из пяти атомных орбиталей, которые определенным образом расположены в пространстве (рис. 2), и обозначаются соответственно.

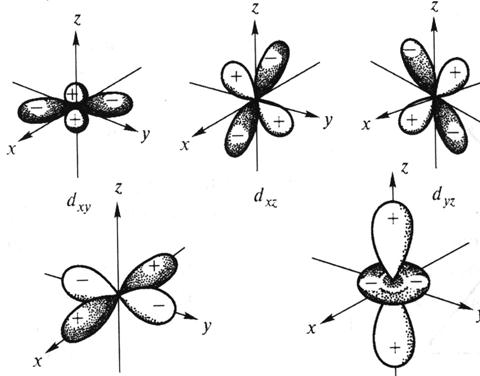
Рис. 2. Пространственная форма d-атомных орбиталей.

Четыре из пяти d- орбиталей имеют форму четырехлепестковых розеток, каждая из которых образована двумя гантелями, пятая АО представляет собой гантель с тором в экваториальной плоскости (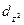-орбиталь) и расположена вдоль оси z. Лепестки орбитали 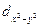расположены вдоль осей x и y. Лепестки орбиталей 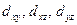расположены симметрично между соответствующими осями.

Четвертый энергетический уровень состоит из четырех подуровней – s, p, d и f. Первые три из них аналогичны описанным выше, а четвертый f -подуровень состоит из семи АО, пространственная форма которых достаточно сложна и в данном разделе не рассматривается.

С. Гаудсмит и Дж. Уленбек для описания некоторых тонких эффектов в спектре атома водорода в 1925 г. выдвинули гипотезу о наличии собственного момента импульса электрона, который назвали спином. Спин нельзя выразить через координаты и импульсы, у него нет аналога в классической механике. Спиновое число s электрона принимает только одно значение, равное 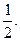Проекция вектора спина на определенное направление внешнего поля (например, на ось z) определяется спиновым квантовым числом m_S, которое может принимать два значения: m_S =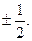

Понятие «спин» введено для характеристики специфического квантового свойства электрона. Спин – это проявление релятивистских эффектов на микроскопическом уровне.

Электрон имеет четыре степени свободы. Спиновое квантовое число принимает только дискретные значения: 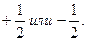Таким образом, состояние электрона в атоме определяется набором значений четырех квантовых чисел: n, l, m_l, m_S.

Обозначение и структура электронных энергетических уровней. Определим некоторые термины, которые используются для разъяснения физического смысла квантовых чисел. Группа орбиталей, имеющих одинаковое значение орбитального квантового числа, образует энергетический подуровень. Совокупность всех орбиталей с одинаковым значением главного квантового числа образует энергетический уровень.

Структуру атомных электронных уровней можно изобразить двояко: в виде электронных формул и электронографических диаграмм. При написании электронных формул используют два квантовых числа n и l: первый уровень – 1 s; второй – 2 s, 2 p; третий – 3 s, 3 p, 3 d; четвертый – 4 s, 4 p, 4 d, 4 f и т.д. (табл.3).

Таблица 3

Структура электронных энергетических уровней атома

Главное квантовое число n	Обозначение подуровня	Квантовое число
l	ml
	1 s 2 s 2 p 3 s 3 p 3 d 4 s 4 p 4 d 4 f		-1, 0, +1 -1, 0, +1 -2, -1, 0, +1, +2 -1, 0, +1 -2, -1, 0, +1, +2 -3, -2, -1, 0, +1, +2, +3

Более полно строение электронных уровней описывается с использованием трех квантовых чисел: n, l, m_l. Каждая АО условно изображается в виде квантовых ячеек, около которой ставится номер уровня и символ подуровня.

Дата добавления: 2014-01-04