Метод простой итерации для системы двух нелинейных уравнений

Решаем два нелинейных уравнения с двумя неизвестными:

(3.4)

Действительные корни надо найти с заданной точностью .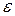

Систему (3.4) преобразуем к виду:

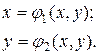(3.5)

Графически или другой грубой прикидкой определяем начальные приближения 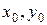. Итерационный процесс, то есть последовательные приближения, выполняются по формулам:

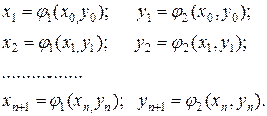(3.6)

Если итерационный процесс (3.6) сходится, то при некотором числе итераций n, выполняется условие:

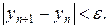и (3.7)

При выполнении (3.7) вычисления прекращают. Искомые корни .

При создании программы для ПК необходимо предусмотреть ограничение числа итераций, так как вычислительный процесс может расходиться.

Пример: решить систему уравнений

} (3.8)

Необходимо определить положительные корни с точностью . Поэтому вычисления выполняем с 3-мя цифрами после запятой.

Начальные приближения 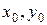определяем графически. Для этого из первого и второго уравнения выражаем :

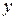Задаем 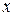с равным шагом и выполняем вычисления по формулам (3.9) и (3.10). Результаты заносим в табл. 3.2. По таблице строим два графика (см. рис. 3.5). Точка пересечения графиков дает приближенные начальные значения

Все эти расчеты и построения выполняем с использованием Excel.

Таблица 3.2

Результаты расчетов по формулам (3.9) и (3.10)

x	у по формуле (3.9)	у по формуле (3.10)
0,9	-2,09	0,87
1,3	-1,63	1,28
1,7	-1,01	1,55
2,1	-0,32	1,75
2,5	0,40	1,92
2,9	1,14	2,07
3,3	1,90	2,20

Рис. 3.5. Графики, построенные по формулам (3.9) и (3.10)

Теперь из исходной системы (3.8) получаем формулы вида (3.5):

} (3.11)

Запись формул (3.11) в виде, удобном для построения итерационного процесса:

} (3.12)

Здесь n – номер итерации. Вычисления по формулам (3.12) приведены в табл.

Таблица 3.12

Значения последовательных приближений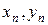

n
	3,5	2,2
	3,479	2,259
	3,481	2,260
	3,484	2,261
	3,486	2,261
	3,487	2,262
	3,487	2,262

Корни найдены (, так как выполняется условие (3.7).

Замечание: вместо рассмотренного принципа последовательных приближений (3.6), иногда удобнее пользоваться процессом Зейделя:

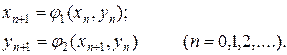
Если рассматривается система из 3-х уравнений:

Дата добавления: 2014-01-04