Основные понятия. К решению систем линейных уравнений сводится многочисленные практические задачи

К решению систем линейных уравнений сводится многочисленные практические задачи. Можно утверждать, что решение линейных уравнений является одной из самых распространенных и важных задач вычислительной математики (численных методов).

Запишем систему из n линейных алгебраических уравнений, с n неизвестными:

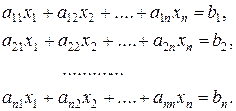} (4.1)

Коэффициенты этой системы образуют квадратную матрицу:

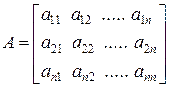. (4.2)

Обозначим: Х - вектор-столбец неизвестных х_i; В - вектор-столбец свободных членов системы (4.1) b_i (i = 1, 2, …, n). Тогда

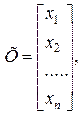
(4.3)

Система уравнений (4.1) в матричном виде:

А*Х=В. (4.4)

Определителем матрицы А называется число D, равное:

Необходимым и достаточным условием существования единственного

решения системы линейных уравнений является условие .

Методы решения систем линейных уравнений делятся на прямые и итерационные. Прямые методы используют конечные формулы для вычисления неизвестных. Они дают решение после выполнения заранее известного количества операций. Эти методы сравнительно просты и универсальны. Пример – метод Крамера.

Однако прямые методы имеют ряд недостатков. Наиболее существенным является накапливание погрешностей в процессе решения, т.к. вычисления на любом этапе используют результаты предыдущих операций. Погрешности накапливаются из-за отбрасывания в ЭВМ младших разрядов чисел. Это особо опасно для больших систем (n > 200), а так же для плохо обусловленных систем (D близок к нулю, очень мал). Прямые методы не используют так же для систем с плохо заполненной матрицей (много нулей).

Итерационные методы – это методы последовательных приближений. В них необходимо задать некоторое приближенное решение – начальное приближение. После этого по определенному алгоритму проводится один цикл вычислений, называемый итерацией. В результате итерации находят новое приближение. Итерации проводятся до получения решения с заданной точностью. Алгоритмы решения линейных систем уравнений с использованием итерационных методов обычно более сложные по сравнению с прямыми методами. Объем вычислений заранее определить трудно.

Тем не менее, итерационные методы в ряде случаев предпочтительнее. Например, погрешности окончательных результатов при их использовании не накапливаются т.к. точность вычислений в каждой итерации определяется лишь результатами предыдущей итерации и практически не зависит от ранее выполненных вычислений.

Для реализации итерационных методов часто требуется меньше памяти ПК по сравнению с использованием прямых методов.

Эти достоинства итерационных методов делают их особенно полезными в

случае большого числа уравнений, а также плохо обусловленных систем.

Следует отметить, что сходимость итераций может быть очень медленной; поэтому ищутся эффективные пути ее ускорения.

Дата добавления: 2014-01-04