Интерполяционный многочлен Лагранжа

Рассмотрим случай глобальной интерполяции, т.е. построение интерполяционного многочлена единственного для всего отрезка [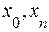]. При этом, естественно, график интерполяционного многочлена должен проходить через все заданные точки.

Искомый многочлен запишем в следующем виде:

φ(х) = , (5.10)

где n – количество узлов интерполяции.

Значения этого многочлена в узлах 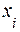должны быть равны соответствующим табличным значениям 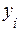. Из данного условия получим систему уравнений для нахождения коэффициентов :

. (5.11)

Решив эту систему линейных уравнений относительно неизвестной (i = 0, 1, …, n) построим многочлен (5.10). Такой путь вычислений трудоемок особенно при большом числе узлов. Существуют более простые алгоритмы вычисления интерполяционного многочлена.

Будем искать многочлен в виде линейной комбинации многочленов степени n:

L(х) =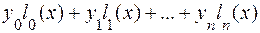. (5.12)

При этом потребуем, чтобы каждый многочлен обращался в 0 во всех узлах интерполяции, за исключением одного i - го, где он должен равняться 1.Этим условиям отвечает многочлен вида (i = 0)

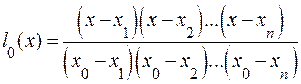. (5.13)

Здесь х – значение аргумента, при котором нужно определить функцию f(х)= =L(х); 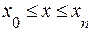; 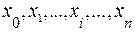- узлы интерполяции (в них функция f(х) известна).

Действительно, в (5.13) 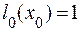при . При 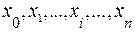числитель и вся дробь обращается в 0.

По аналогии с (5.13) запишем для i = 1 и i = 2:

; (5.14)

. (5.15)

Запись многочлена в общем виде:

. (5.16)

Подставив (5.16) в (5.12), получим:

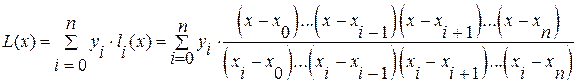. (5.17)

Эта формула называется интерполяционный многочлен Лагранжа.

Из (5.17) можно получить формулы для линейной (n = 1) и квадратичной (n = 2) интерполяции:

n=1

L(х) = ; (5.18)

n=2

; (5.19)

Рассмотрим числовой пример. Пусть в таблице задано только три значения предела прочности 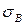(МПа) в зависимости от температуры t (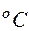) (табл. 5.2).

Таблица 5.2

Зависимость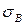= f(t)

t

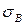
Необходимо определить 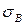при t = 50 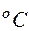. Это и есть величина L(х). Таким образом, х = 50; х₀=20; х₁=100; х₂=200; у₀=470; у₁=450; у₂=460. Расчет выполняем по формуле (5.19):

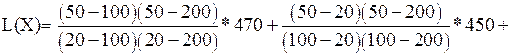
Предел прочности 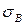=459,6 МПа при температуре t = 50 .

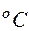Дата добавления: 2014-01-04