Постановка задачи. Подбор эмпирических формул

Подбор эмпирических формул

При интерполировании функций мы использовали условие равенства значений интерполяционного многочлена и данной функции в известных точках - узлах интерполяции. Однако в ряде случаев выполнение этого условия нецелесообразно. Например, в случае обработки опытных данных нужно иметь в виду ошибки этих данных. Они могут быть вызваны несовершенством измерительного прибора, субъективными причинами, различными случайными факторами и т. д.

Построение аппроксимирующего многочлена с условием обязательного прохождения его графика через экспериментальные точки означало бы тщательное повторение допущенных при измерении ошибок. Выход из этого положения может быть найден выбором такого многочлена, график которого проходит близко от экспериментальных точек. Понятие «близко» уточняется при рассмотрении различных видов приближения (аппроксимации).

Одним из таких видов является среднеквадратичное приближение функций с помощью аппроксимирующего многочлена

φ(х) = , (6.1)

где m – степень многочлена; n – количество опытных точек.

При среднеквадратичном приближении m < n. Случай m = n соответствует глобальной интерполяции. На практике стараются подобрать аппроксимирующий многочлен как можно меньшей степени. Как правило, m = 1, 2, 3.

Аппроксимирующий многочлен называют также эмпирической формулой. Это формула, полученная путем описания (приближения) опытных данных.

Графики интерполяционного и аппроксимирующего многочленов показаны на рис. 6.1. На этом рисунке ε_i - отклонение между значениями опытных данных (y_iэ) и аппроксимирующим многочленом (y_i) в точке x_i. т.е.

.

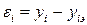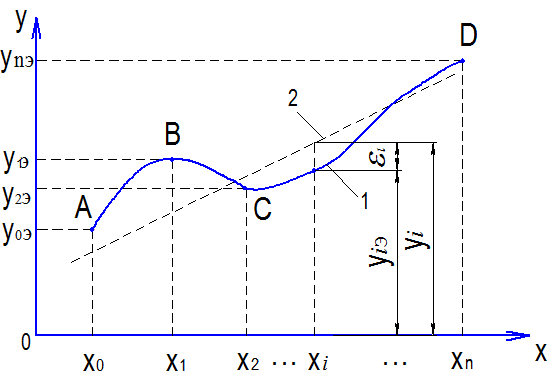
Рис. 6.1. Интерполяция и среднеквадратичное приближение (аппроксимация):

A,B,C,D - опытные точки; 1 – график интерполяционного многочлена;

2 - график аппроксимирующего многочлена (найденного среднеквадратичным приближением)

Мерой отклонения многочлена φ(х) от заданной функции f(х) на множестве точек (х_i, y_i) (i = 0, 1, 2, …, n) при среднеквадратичном прибавлении является величина S:

, (6.2)

где S - сумма квадратов отклонений между значениями многочлена и функции в данных точках (или сумма квадратов отклонений между опытными данными и рассчитанными по формуле (6.1)); y_iэ – опытные значения функции f(x) при х = х_i.

Для построения аппроксимирующего многочлена (эмпирической формулы) (6.1) коэффициенты a₀, а₁ , …,а_m нужно подобрать так, чтобы величина S была наименьшей. В этом состоит метод наименьших квадратов.

Дата добавления: 2014-01-04