Определение реакции линейной многомерной управляемой системы с помощью преобразования Лапласа

Операционная структурная схема управляемой системы.

Операционная структурная схема – блок-схема, которая является графическим отображением уравнений системы в переменных состояния (модели типа «вход – состояние – выход»).

Динамическая структурная схема – графическое отображение уравнений системы типа «вход – выход» (т. е. используя передаточные функции звеньев, проходили в прошлом семестре).

Рассмотрим операционную структурную схему. Чтобы отобразить уравнения в переменных состояния (1) и(2) надо иметь четыре вида элементов, которые производят элементарные операции:

1. Усилитель с матричным коэффициентом А:

2. Интегратор векторных сигналов

отображает уравнение

,

где x (t ₀) – начальное состояние,

линия передачи векторного сигнала,

линия передачи скалярного сигнала.

3. Сумматор векторных сигналов:

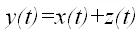
4. Точка разветвления сигнала:

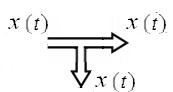
Отобразим уравнения

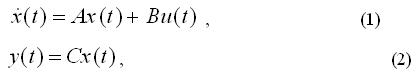
с помощью операционной структурной схемы:

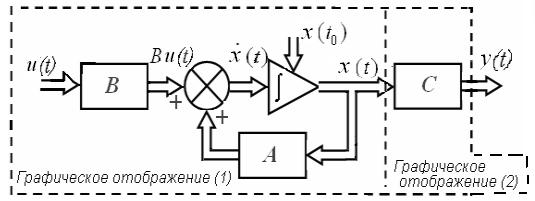
Операционные структурные схемы, отображающие уравнения (*) и (**), тоже имеют большое значение не только для теории, но и симуляции (динамического моделирования) управляемых систем. Схемы моделирования в современных пакетах, например Simulink, по сути дела представляют собой «живые» операционные структурные схемы систем, описываемых подобными уравнениями.

Для примера построим операционную структурную схему двойного интегратора, описываемого уравнениями

Схема в Simulink показана ниже

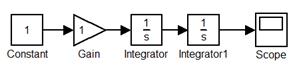
Одной из важных задач анализа является определение реакции многомерной управляемой системы на входной сигнал.

Дано: Модель типа «вход – состояние – выход»

, (1)

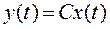. (2)

Известно управление u (t) для t > t ₀ и начальное состояние x (t ₀)= x _0.

Найти: Выходной сигнал у (t), t > t _0.

Решим эту задачу с помощью преобразования Лапласа. Пусть t ₀=0.

Преобразуем по Лапласу уравнение (1). Все теоремы о преобразовании Лапласа скалярных величин справедливы и для векторных величин.

Используя теорему линейности, получаем

.

Обозначим преобразование Лапласа вектора состояния и преобразование Лапласа управления .

Используя теорему об изображении производной

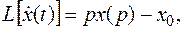
получаем

, (*)

где I – единичная матрица ().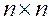

Введем в рассмотрение резольвенту , матрицу (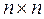). Умножая слева уравнение (*) на резольвенту, получаем изображение по Лапласу вектора состояния

.

Определяя обратное преобразование Лапласа, находим решение уравнения (1):

.

Если учтем, что 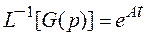- матричная экспонента и воспользуемся теоремой об изображении свертки двух функций, получим

. (**)

Дата добавления: 2014-01-04