Прямое решение линейных разностных уравнений

Линейное разностное уравнение описывает связь выхода и входа Д-фильтра лишь в неявной форме. Чтобы найти его реакцию на некоторую входную последовательность, надо это уравнение решить. Здесь, как и для непрерывных систем, знание поведения входной последовательности u [ i ] для

i = 0, 1, 2, ... и равенство ее нулю при i< 0 позволяют получить лишь частичное описание выходной последовательности y [ i ] при i = 0, 1, 2. Для системы порядка n необходимо иметь n дополнительных данных, соответствующих начальным условиям в непрерывном случае. Однако в отличие от ситуации с дифференциальными уравнениями определение реакции Д-фильтра оказывается более простым делом. Покажем это, выразив уравнение (1) через последовательности, смещенные в сторону запаздывания. Заменяя в

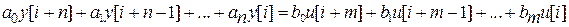(1)

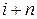() на i, т.е. полагая 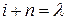, а затем, обозначая 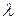как i, получаем другую форму записи разностного уравнения Д-фильтра

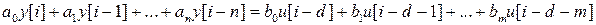, (2)

где 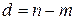. Здесь

, , , ,

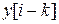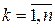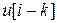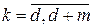представляют собой соответственно последовательности выхода и входа, смещенные в сторону запаздывания на k периодов дискретизации.

Полагая 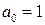, из (2) получаем рекуррентное соотношение

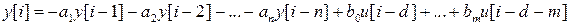, (3)

позволяющее определять выходную последовательность y [ i ], другими словами, реакцию Д-фильтра на входную последовательность u [ i ].

Отметим, что для уравнения (3) начальными условиями являются значения y [ - 1], y [ - 2], …, y [ -n ], которые будем считать заданными.

За начальный момент времени принимаем i= 0.

Если хотя бы одно из значений y [ - 1], y [ - 2], …, y [ -n ] не равно нулю, то говорят, что Д-фильтр предварительно возбужден.

Если y [ - 1] =y [ - 2] =…=y [ -n ] = 0, то говорят, что Д-фильтр предварительно невозбужден.

Поставим задачу:

Пусть известна входная последовательность u [ i ] и начальные условия. y [ - 1], y [ - 2], …, y [ -n ].

Требуется найти реакцию 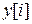Д-фильтра для i = 0, 1, 2, 3, ....

Эту задачу можно решить с помощью прямого метода в силу того, что ЛРУ (3) является рекуррентным соотношением. Полагая i= 0, из уравнения

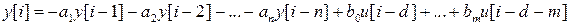(3)

получаем

,

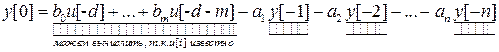Значение y[0] можно вычислить, т.к. u[i] задано, а начальные условия 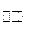известны.

Положим i= 1 в (3), получаем

,

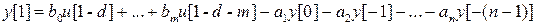(значение y[0] найдено на предыдущем шаге) и т. д. вычисляем y [2], y [3] ,…

Недостаток: ошибки округления.

Дата добавления: 2014-01-04