Дифференциальные зависимости между изгибающим моментом (М), поперечной силой (Q) и интенсивностью распределённой нагрузки(q)

Рассмотрим простейшую балку.

Выделим из балки элемент двумя поперечными сечениями длинной dx.

Действие правой части (отброшенной) заменим Q и М, но уже с добавкой за счет приращение. Составим уравнение равновесия для элемента (т.к. балка в равновесии, то и все элементы её в равновесии).

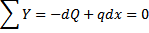
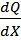= q. (1)

Первая производная от поперечной силы, по абсциссе сечения x численно равна интенсивности распределённой погрузки q.Запишем момент относительно точки О.

Σ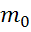=-dM+Qdx+dx * 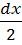=0.

Пренебрегая малыми высших порядков, получаем

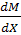= Q. (2)

Первая производная от изгибающего момента, по абсциссе сечения x численно равна поперечной силе.

Из соотношений (1) и (2) вытекает третья зависимость

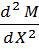=q. (3)

Выводы, вытекающие из дифференциальных зависимостей и метода сечений

1. Тангенс угла образованного x и касательной к эпюре Q в данной точке равен интенсивности распределённой нагрузки

tg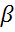= =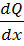q.

2. Тангенс угла образованного осью x и касательной у эпюре M в данной точке численно равен поперечной силе

tg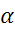= =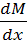Q.

3. Если на участке балки:

а) Q>0, то момент (M↗) возрастает слева на право.

б) Q<0, то момент (M↘) убывает слева на право.

в) Q-переходит через 0 изменяя знак с «+» на «-», то M= 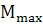, при изменении знака Q c «-» на «+» M=.

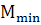г) Если Q=0, то M=const – следовательно, имеем чистый изгиб.

4. Если на участке балки интенсивность распределённой нагрузки q=0, то на этом участке эпюра «Q» ограниченна прямой параллельной оси x, а эпюра «M» ограниченна прямой наклонной к оси x.

5. Если на участке q=const, то на этом участке эпюра «Q» ограниченна прямой наклонной к оси x, а эпюра «M» ограниченна квадратной параболой с выпуклостью в сторону действия распределённой нагрузки (правило дождя).

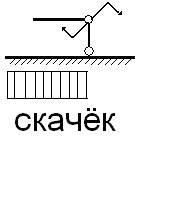
6. Под сосредоточенной силой на эпюре «Q» имеет место скачёк на величину силы, а на эпюре «M» перелом в сторону действия силы.

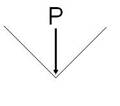
7. Под сосредоточенным моментом на эпюре «M» имеет место скачёк на величину момента, а на эпюре «Q» это непосредственно не отражается.

8. В шарнирах изгибающие моменты равны нулю, если там не приложены внешние пары сил

9. Между M, Q, q существует интегральные зависимости. Возьмём участки балки.Знаем 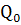, 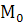в начале участка. На участке от 0 до х имеем

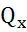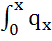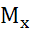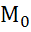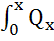=dx+,

=+dx=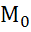+W; из дифференциальной зависимости

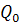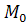,- поперечная сила и изгибающий момент в начале участка,W – площадь эпюры «Q».

Дата добавления: 2014-01-04