
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы о среднем значении
|
|
|
|
Лекция 18. Теоремы о среднем значении.
Определение 18.1. Функция  достигает в точке
достигает в точке 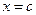 локального максимума (минимума), если существует окрестность
локального максимума (минимума), если существует окрестность  этой точки, на которой выполняется неравенство
этой точки, на которой выполняется неравенство 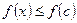 или
или  для
для 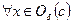 (соответственно
(соответственно  или
или  для
для 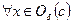 ). Локальный максимум и локальный минимум называются локальным экстремумом.
). Локальный максимум и локальный минимум называются локальным экстремумом.
☼ Замечание 18.1. Если функция  непрерывна на отрезке непрерывна на отрезке  и достигает на нём максимума (минимума) в точке и достигает на нём максимума (минимума) в точке  , то, очевидно, точка c является в то же время точкой локального максимума (минимума) , то, очевидно, точка c является в то же время точкой локального максимума (минимума)  . Другое дело, если максимум (минимум) . Другое дело, если максимум (минимум)  на на  достигается в одной из концевых точек отрезка. Такая точка не является точкой локального максимума (минимума) достигается в одной из концевых точек отрезка. Такая точка не является точкой локального максимума (минимума)  , т.к. , т.к.  не определена в полной окрестности концевых точек (см. рис. 18.1). ☼ не определена в полной окрестности концевых точек (см. рис. 18.1). ☼
|  Рис. 18.1.
Рис. 18.1.
|
♦ Теорема 18.1 (Ферма [1]). Пусть функция  определена на интервале
определена на интервале  . Если функция
. Если функция  имеет производную в точке
имеет производную в точке  и достигает в этой точке локального экстремума, то
и достигает в этой точке локального экстремума, то  .
.
Доказательство. Для определённости будем считать, что  имеет в точке c локальный максимум. По определению производной
имеет в точке c локальный максимум. По определению производной 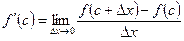 .
.
Так как для 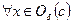
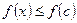 , то
, то  при
при  , т.е.
, т.е.
 . (18.1)
. (18.1)
Если же  , то
, то  , т.е.
, т.е.
 . (18.2)
. (18.2)
Из (18.1) и (18.2) вытекает, что  . ■
. ■
♦ Теорема 18.2 (Ролля [2]). Если функция  непрерывна на
непрерывна на  , дифференцируема на
, дифференцируема на  и
и  , то существует, по крайней мере одна, точка
, то существует, по крайней мере одна, точка  такая, что
такая, что  .
.
Доказательство. 1) Если  постоянна на
постоянна на  , то для всех
, то для всех  производная
производная  .
.
2) Будем считать, что  непостоянна на
непостоянна на  . Т.к.
. Т.к.  непрерывна на
непрерывна на  , то существует точка
, то существует точка  , в которой
, в которой  достигает максимума на
достигает максимума на  , и существует точка
, и существует точка 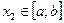 , в которой
, в которой  достигает минимума на
достигает минимума на  .
.
Обе точки  ,
,  не могут быть концевыми точками, иначе
не могут быть концевыми точками, иначе

и  была бы постоянной на
была бы постоянной на  . Следовательно, одна из точек
. Следовательно, одна из точек  ,
,  принадлежит интервалу
принадлежит интервалу  . Обозначим её
. Обозначим её 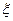 . В ней достигается локальный экстремум. Кроме того,
. В ней достигается локальный экстремум. Кроме того,  существует, потому что по условию
существует, потому что по условию 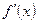 существует для всех точек
существует для всех точек 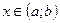 . Поэтому, по теореме Ферма
. Поэтому, по теореме Ферма  . ■
. ■
☼ Замечание 18.2. Теорема Ролля сохраняет силу также для интервала  , лишь бы выполнялось соотношение , лишь бы выполнялось соотношение  . ☼
☼ Замечание 18.3. Теорема Ролля имеет простой геометрический смысл. Если выполнены условия теоремы, то на графике функции . ☼
☼ Замечание 18.3. Теорема Ролля имеет простой геометрический смысл. Если выполнены условия теоремы, то на графике функции  существует точка существует точка  , касательная в которой параллельна оси Ox. (см. рис. 18.2). ☼ , касательная в которой параллельна оси Ox. (см. рис. 18.2). ☼
| 
|
Рис.18.2.
♦ Теорема 18.3 (Коши [3]). Если функции  и
и  непрерывны на
непрерывны на  , дифференцируемы на
, дифференцируемы на  и
и 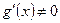 в
в  , то существует точка
, то существует точка  такая, что
такая, что  .
.
Доказательство. Заметим, что 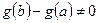 , т.к. иначе по теореме Ролля нашлась бы точка
, т.к. иначе по теореме Ролля нашлась бы точка 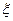 :
:  , чего не может быть по условию теоремы.
, чего не может быть по условию теоремы.
Составим вспомогательную функцию 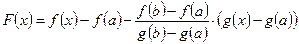 . Функция
. Функция  непрерывна на
непрерывна на  , дифференцируема на
, дифференцируема на  и
и 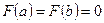 (проверить!). По теореме Ролля существует точка
(проверить!). По теореме Ролля существует точка  , в которой
, в которой  . Но
. Но  . Подставим
. Подставим 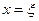 и получим, что
и получим, что  . ■
. ■
☼ Замечание 18.4. В формуле Коши необязательно  , можно взять
, можно взять  . ☼
. ☼
♦ Теорема 18.4 (Лагранжа [4]). Пусть функция  непрерывна на
непрерывна на  , имеет производную на
, имеет производную на  . Тогда существует точка
. Тогда существует точка  для которой
для которой 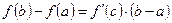
 .
.
Доказательство. Введём функцию  . Функция
. Функция  удовлетворяет условиям теоремы Ролля: 1) непрерывна на
удовлетворяет условиям теоремы Ролля: 1) непрерывна на  ; 2) дифференцируема на
; 2) дифференцируема на  ; 3)
; 3) 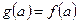 ,
, 
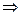
 . Следовательно, существует точка
. Следовательно, существует точка  :
:  . Но
. Но  и получаем, что
и получаем, что  ,
, 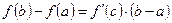 . ■
. ■
☼ Замечание 18.5. Теорему Лагранжа можно доказать как следствие теоремы Коши, взяв  .
.
Теорема Лагранжа имеет простой геометрический смысл. Запишем её в виде
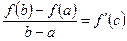
 . (18.3)
. (18.3)
Левая часть равенства (18.3) – это тангенс угла наклона к оси Ox хорды, стягивающей точки  и и  графика функции графика функции  , а правая часть – тангенс угла наклона касательной к графику в некоторой промежуточной точке с абсциссой , а правая часть – тангенс угла наклона касательной к графику в некоторой промежуточной точке с абсциссой  . Таким образом, если кривая есть график непрерывной на . Таким образом, если кривая есть график непрерывной на  функции, имеющей производную на функции, имеющей производную на  , то на этой кривой существует точка, соответствующая некоторой абсциссе , то на этой кривой существует точка, соответствующая некоторой абсциссе  , такая что касательная в этой точке параллельна хорде, стягивающей концы кривой , такая что касательная в этой точке параллельна хорде, стягивающей концы кривой  и и  . .
|  Рис. 18.3.
Рис. 18.3.
|
Формула (18.3) называется формулой конечных приращений. Промежуточное значение c удобно записывать в виде 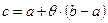 , где
, где  . Формула Лагранжа:
. Формула Лагранжа:
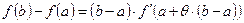 .
.
Она верна не только для  , но и для
, но и для  . ☼
. ☼
J Пример 18.1. Оценим  .
.
 . По теореме Лагранжа
. По теореме Лагранжа
 . J
. J
♦ Теорема 18.5. 1) Функция  , непрерывная на отрезке
, непрерывная на отрезке  и имеющая неотрицательную (положительную) производную на интервале
и имеющая неотрицательную (положительную) производную на интервале  , не убывает (строго возрастает) на отрезке
, не убывает (строго возрастает) на отрезке  .
.
Доказательство. Пусть  . По теореме Лагранжа существует точка
. По теореме Лагранжа существует точка  , для которой
, для которой  . Если
. Если  , то
, то 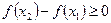
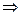
 – функция
– функция  не убывает. Если
не убывает. Если 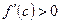 , то
, то 
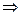
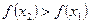 – функция
– функция  строго возрастает. ■
строго возрастает. ■
♦ 2) Функция  , непрерывная на отрезке
, непрерывная на отрезке  и имеющая неположительную (отрицательную) производную на интервале
и имеющая неположительную (отрицательную) производную на интервале  , не возрастает (строго убывает) на отрезке
, не возрастает (строго убывает) на отрезке  .
.
Доказательство аналогично пункту 1). ■
J Пример 18.2. Функция  имеет непрерывную производную
имеет непрерывную производную  для
для  .
.
 ,
,  .
.
Следовательно, она (функция) строго возрастает и непрерывно дифференцируема на  . Поэтому она имеет обратную однозначную непрерывно дифференцируемую функцию
. Поэтому она имеет обратную однозначную непрерывно дифференцируемую функцию  ,
,  . J
. J
♦ Теорема 18.6. Если функция  имеет на интервале
имеет на интервале  производную, равную нулю, то она постоянна на
производную, равную нулю, то она постоянна на  .
.
Доказательство. По теореме Лагранжа  ,
,  – фиксированная точка, x – произвольная точка,
– фиксированная точка, x – произвольная точка, 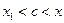 (или
(или  ). Так как
). Так как  , то
, то  и
и  для
для  . ■
. ■
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 820; Нарушение авторских прав?; Мы поможем в написании вашей работы!