Лекция 18

Поле классов вычетов по модулю

Рассмотрим пример нечислового поля 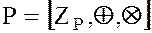– поля классов вычетов по модулю .

Теорема. Кольцо классов вычетов 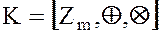является полем тогда и только тогда, когда – простое число.

Теорема будет доказана, если мы покажем, что при выполняются следующие условия:

1. Множество классов вычетов – – не содержит делителей нуля;

2. .

Доказательство. Пусть – не простое число.

Это означает, что 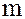можно представить в виде

,

тогда

.

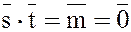Это означает, что и являются делителями нуля в .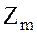

Пусть 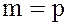– простое число, тогда, множество классов вычетов принимает вид:

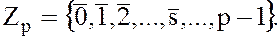(4)

Обозначим все элементы множества 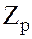отличные от нуля :

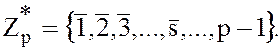(5)

Эти элементы образуют конечную мультипликативную группу: операция умножения на множестве 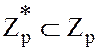ассоциативна и существует единичный элемент, равный .

Обозначим эту группу.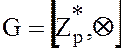

Рассмотрим отображение конечной

мультипликативной группы 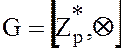саму на себя, которое определим

,

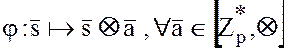где - произвольный, но фиксированный элемент из .

Применяя отображение к множеству из (5), получаем множество

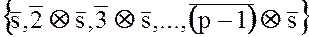(6)

Все элементы множества (6) отличны от нуля и все различны:

при

Предложим обратное. Если

,

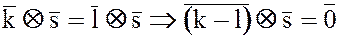это возможно только при .

Это означает, что последовательность (6) совпадает с переставленной некоторым образом последовательностью (5), следовательно в последовательности (6)

.

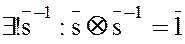Это означает, что является обратным к , а т.к.

– произвольный элемент из 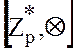, то это и доказывает теорему.

Следствие 1. (малая теорема Ферма). Для любого целого 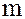, не делящегося на простое , имеет место сравнение

. (7)

Доказательство. 1. Мультипликативная группа 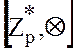имеет порядок .

По теореме Лагранжа порядок этой группы делится на порядок любого элемента из группы .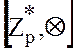

2. Из следствия теоремы Лагранжа следует, что группа простого порядка всегда циклическая, а порядок любого элемента циклической группы совпадает с порядком группы.

Следовательно, любой элемент 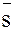группы 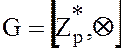в степени будет равен единичному элементу, т.е. .

С другой стороны, 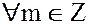, если 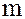не делится на , то его можно представить в виде 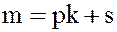, где , т.е. совпадает с одним из элементов группы .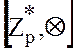

Следовательно,

.

Следствие 2. Для любого целого 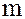имеет место сравнение

(8)

Доказательство. Действительно, умножая обе части сравнения (7) на 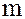, получим

.

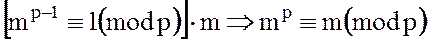Этот результат имеет место и тогда, когда числа 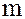и не являются взаимно простыми. Есл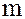и и не взаимно простые числа, то при простом число 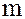делится на .

Тогда 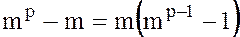также делится на . Поэтому

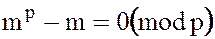или .

Пример1. Пусть m=705, p=7. Доказать, что

Доказательство. Представим m=705=100 7+5.

Порядок группы 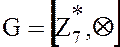равен 6,следовательно

Пример2. Найти остаток от деления числа 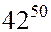на 17.

Поскольку 17 и 42 взаимно простые числа, то по малой теореме Ферма

.

Возводя в третью степень обе части сравнения, получаем

.

Кроме того,

,

а в квадрате это дает

.

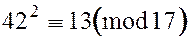Перемножая полученные сравнения, находим 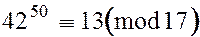. Таким образом, искомый остаток равен 13.

Дата добавления: 2014-01-04