Лекция 11. Решение транспортной задачи

«методом потенциалов».

Метод потенциалов - одна из разновидностей симплекс-метода, проводимого непосредственно в распределительной таблице: здесь так же вначале ведётся поиск начального опорного решения, а затем после поиска полезной свободной клетки проводят направленные итерации по получению решений с всё меньшим и меньшим значением целевой функции, вплоть до нахождения оптимального решения.

Отличие в рассматриваемом методе заключается только в том, что вместо «оценок клеток» (как известно, рекомендуется выполнять построение циклов со свободными клетками, имеющими отрицательные оценки) будут фигурировать нарушения потенциалов в некоторых свободных клетках.

Нарушения потенциала со знаком плюс в некоторой свободной клетке будет свидетельствовать о том, что с ней можно организовать цикл однократного замещения, ведущий к уменьшению значения целевой функции.

Попутно замётим, что численное значение нарушения потенциала (но с противоположным знаком) в точности равно отрицательной оценке той же самой свободной клетки.

Потенциалы клеток, занятых базисными переменными, в точности равны сумме потенциалов i -ой строки и j -го столбца, поскольку это является исходным условием для понятия потенциалов:

П_ij^баз = u_i + v_j(11.1)

Нарушение потенциала для свободной клетки констатируется в том случае, если:П_ij^св. > с _ij^св(11.2.)

с _ij^св – значение единичной стоимости, записанное в клетке

Численное значение нарушения потенциалов ΔП_ij равно:

ΔП_ij = П_ij^св. - с _ij^св = - о _ij^св

Опорное решение в данном алгоритме рекомендуем определять методом минимального элемента (табл. 11.1.).

Таблица 11.1

Z₀ = 970. Исходное опорное решение

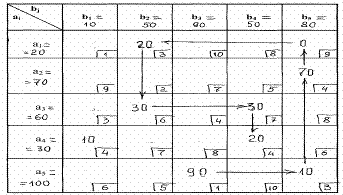
Стрелками показан “маршрут» прохождения клеток с минимальными элементами, начиная с клетки (5 - 3) с минимальным значением единичной стоимости. Метод минимального элемента обеспечил меньшее значение целевой функции, чем метод северо-западного угла в исходной таблице.

Рассмотрим теперь порядок определения потенциалов и нарушения потенциалов ΔZ_ij по свободным клеткам (табл. 11.2.).

Таблица 11.2

Схема определения потенциалов клеток

В приводимой таблице клетки, занятые базисными переменными заштрихованы. В кружочках рядом с потенциалами показана очерёдность их

нахождения, начиная с первого, который обязательно назначается равным нулю (с какой строчки начинать, в принципе) не имеет значения. Но удобней с первой строчки.

Ввиду того, что для данного расчёта нам не нужны «значения корреспонденций» в занятых клетках мы просто заштриховали названные клетки, чтобы обозначить их расположение в таблице. Продолжаем горизонтальную стрелку по первой строке (это горизонтальная составляющая потенциала) до затенённой клетки и останавливаемся в клетке (1-2). Далее поворачиваем её ход по вертикали вниз, за границы таблицы.

Там мы должны записать вертикальную составляющую потенциала с таким значением, чтобы сумма горизонтальной и вертикальной составляющей в точностисовпадали со значением единичной стоимости, записанной в уголкезатенённой клетки.

В нашем случае это будет число «3». Здесь же в кружочке запишем номер нашего действия – это цифра 2. Названная только что стрелка «пронзает» также клетку (1.5.). В третьей процедуре (порядковый номер 3), мы записываем цифру «9». Действие под номером 4 (в кружочке ) выводит своей горизонтальнойстрелкой наклетку (2-5). Здесь инициатива идёт уже от клетки (2-4) и для обеспечения нулевого баланса единичной стоимости мы записываем горизонтальную составляющую потенциала в размере «- 5». Метод потенциалов, при наличии навыков, позволяет намного быстрее прийти к опорному решению, в том числе за счёт отпадания надобности в проведении циклических преобразований. Мы сразу, в процессе заполнения таблицы потенциалами обнаруживаем свободные клетки, которые обеспечивают полезное циклическое преобразование от новой свободной клетки.

Следует иметь в виду, что после проведения очередной итерации, описанная схема расчёта повторяется заново с каждым, очередным, опорным решением.

Пример табличного расчёта приведен в таблице 11.3. Как и следовало ожидать, численные значения целевых функций в обоих вариантах совпадают по численным значениям целевых функций.

Таблица 11.3

Дата добавления: 2014-01-05