Элементы теории графов

Лекция 12-13. Теория графов и сетевое управление

Резюме.

Задачи линейного программирования являются математическими моделями многочисленных задач технико-экономического содержания. Таковы, например, задачи планирования работы предприятия по выпуску продукции. Предприятие

может выпускать множество видов продукции, но оптимальным будет такой набор её видов, который приносит прибыль: то ли за счёт экономии затрат, то ли за счёт повышения эффективности производства.

Множество задач такого рода могут быть сформулированы как задачи распределения ресурсов и попасть в зону интересов математического программирования, конкретно и в пределы симплекс- метода линейного программирования.

Как правило, в постановке задач по выбору и использованию моделей принимают участие и специалисты математических областей знаний.

Решающую роль в продвижении идей моделирования в практическую отрасль является взаимное проникновение знаний и умений в области математического моделирования и специалистов разных отраслей.

Сетевое планирование и управление (СПУ), или, проще, «сетевые графики», получили широкое распространение в отечественной практике благодаря наглядности этого вида графических моделей.

Теоретической основой для такого представления задач послужила теория графов».

Граф (от греческого 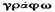- пишу) – это формализованное изображение, составленное из множества V вершин и набора E неупорядоченных и упорядоченных пар вершин. Обозначается граф через G(V, E). Неупорядоченная пара вершин связывается ребром, упорядоченная пара — связывается между собой дугой (дуга фигурирует вместе со стрелочкой, показывающей её направление). Граф, содержащий только рёбра, называют неориентированным, а содержащий только дуги, называют ориентированным. Пара вершин может соединяться двумя или более рёбрами (дугами одного направления), такие рёбра (дуги) называются кратными.

Дуга (или ребро) может начинаться и кончаться в одной и той же вершине, такая дуга (ребро) называется петлёй.

Вершины, соединённые ребром, или дугой, называют смежными.

Рёбра, имеющие общую вершину, также называют смежными, а любые из его двух вершин называются инцидентными.

Говорят, что ребро (u,v) соединяет вершины u и v, и говорят, что дуга (u,v) начинается в вершине « u» кончается в вершине « v».

Каждый граф можно представить в евклидовом пространстве множеством точек, соответствующих вершинам, которые соединены линиями, и эти вершины будут соответствовать ребрам.

Этот класс графов называется плоским, и именно он модифицирован для использования в расчётных моделях сетевого планирования и управления.

Отвлекаясь от содержательной стороны дела, можно рассматривать любой сетевой график как совокупность G некоторого количества точек X₁ Х₂,... и установленных между ними соответствий (связей).

То есть такой объект G называется графом, а точки Х₁, Х₂...— его вершинами, связи между ними - дугами. Граф G считается заданным, если заданы все его вершины и дуги

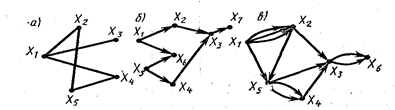
Рис. 12.1.1. Примеры графов

Ориентация дуг, т. е. указание «начала» и «конца» каждой из них, делает граф ориентированным (рис. 12.1.б.). Любые две вершины называются смежными, если их соединяет дуга. Граф, в котором какие-то две вершины соединяются несколькими дугами, называется мультиграфом (рис. 12.1,б).

Дата добавления: 2014-01-05