Лекция 26 Динамическое программирование

Одним из методов решения экстремальных задач, связанных с оптимизацией управления производственными процессами, в том числе на транспорте является динамическое программирование.

Динамическое программирование отличается тем, что не имеет однозначной матема т ической формулировки, В процессе его использования приходится разделить методику вычислений на некоторые последовательные этапы, и после достижения границы очередного этапа снова ставить задачи для достижения новой полезности на новом этапе.

В общих схемах массового обслуживания и решения проблем на основе типичных моделей этот способ решения задач стоит особняком.

С помощью динамического программирования решаются задачи, связанные с процессами, которые можно разделить на некоторое число этапов (шагов). Оптимизация управления на каждом этапе в отдельности не обеспечивает ещё оптимизации процесса в целом.

Алгоритм реализации метода построен на разделение общей задачи на отдельные этапы.

Если число этапов и возможных решений на каждом этапе (управлений) ограничено, то оптимальное решение в целом (оптимальную стратегию) можно найти перебором всех возможных вариантов.

Однако во многих случаях такой путь неприемлем вследствие очень большого числа вариантов.

Динамическое программирование позволяет, не нарушая строгости решения, сократить число рассматриваемых вариантов.

Идея заключается в том, что отыскание экстремального значения функции многих переменных заменяется многократным отысканием экстремальных значений функции одного или небольшого числа переменных.

Для этого вычислительный процесс делится на этапы. Выбирают такое решение задачи, которое позволяет оптимизировать данный этап.

Однако такое решение должно учитывать не только условия этого этапа, но и весь последующий ход процесса, для чего необходимо представлять все решения задачи на последующих этапах.

Поскольку процесс заканчивается на последнем этапе, оптимальное решение не должно учитывать последующего хода. Если найти его для всех ситуаций, которые могут сложиться к началу последнего, то можно получить и конкурирующие решения, из которых можно выбрать наилучшее.

После предварительного выбора всех необходимых инструментов математическая формализация обеспечивает положительный эффект от всех вычислительных процедур.

Принцип оптимальности впервые сформулирован и доказан Беллманом: утверждается, что оптимальная стратегия, начиная с любого этапа, зависит не от предыдущей стратегии, а лишь от состояния системы на данном этапе и последующей стратегии, т. е. от решений на последующих этапах.

Для знакомства с методиками приведём примеры решения задач.

Рассмотрим пример геометрической интерпретации (рис.18.1) метода (источник информации [3]) Смысл её состоит в следующем.

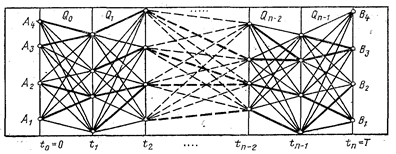
Рис. 18.1. Геометрическая интерпретация задачи

Вертикальным линиям соответствуют моменты времени, в которые рассматривают исследуемую задачу.

В начальный момент t₀ = 0 процесс (система) находится в одном из возможных начальных состояний, множеству которых соответствует множество точек А_i. Начальное состояние может быть задано либо областью возможных состояний, либо одним конкретным значением, в нашем случае четырьмя А ₁ А₂ А₃ и А_4. Будем также считать, для простоты, что в каждый момент времени система находится так же в одном из четырех возможных состояний, которые показаны точками на соответствующих вертикалях.

Конечное состояние системы — одна из четырех точек В₁ В₂ В₃ и В₄

Система переводится из начального состояния в следующее с помощью функции перехода, которую еще называютуправлением системы на данном этапе.Для каждого, из возможных состояний, существует своя функция перехода (или некоторое множество их), которая переводит систему в некоторое множество состояний в следующий момент времени.

Эта функция — количественная характеристика перехода в следующее состояние в зависимости от предыдущего — выражает либо выигрыш, либо затраты. Поскольку значение функции перехода зависит от предыдущего х(i) и от последующего х (i + 1) состояний системы, ее можно записать в общем случае так:

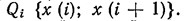
Каждая допустимая стратегия выражается ломаной линией, соединяющей вертикаль t= 0 с вертикалью t_n = Т.

Состоит она из набора управлений на каждом этапе, т. е. ей можно сопоставить число:

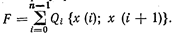
Оптимальной стратегии соответствует ломаная с наименьшим значением F.

Следовательно, исходную задачу можно сформулировать в следующем виде: требуется из всех допустимых ломаных, соединяющих вертикаль t₀₌0 c вертикалью t_n = T выбрать такую, которой соответствует наименьшее значение F.

Решают задачу в таком порядке.

Для всех возможных состояний системы в начале последнего этапа х(n — 1) определяют оптимальное управление — выбирают функцию перехода в одно из

конечных состояний с минимальным значением. Переходы, соответствующие минимальному значению Q_n-1 для каждого состояния (n — 1),показаны на рис. 18.1 жирной линией. Таким образом, в какой бы точке не оказалась система в начале последнего этапа, всегда можно предложить оптимальную стратегию для перевода ее в конечное состояние, получить ряд условно-оптимальных решений. Условие оптимальности каждого такого решения — состояние системы в начале рассматриваемого периода.

Теперь для каждого состояния системы в начале предпоследнего этапа Х(n-2) можно определить условно-оптимальные стратегии для перевода в одно из конечных состояний уже по общему минимуму функций перехода на двух последних этапах: min

При этом значения Q_n-1 уже известны в результате предыдущих вычислений. Затем аналогично определяют условно-оптимальные стратегии на трех последних этапах по условию min(Q_n-2 + Q_n-1), причем Q_n-1 уже известна. Расчеты продолжают до тех пор, пока не будет пройден весь процесс в обратном направлении.

Каждая из полученных ломаных (жирная линия), соответствует условно-оптимальной стратегии для всего процесса. Поскольку множеству начальных состояний системы соответствует множество точек на вертикали, то каждой условно-оптимальной стратегии соответствует свое начальное состояние системы (точка, из которой она выходит). Таким образом, условно-оптимальная стратегия будет оптимальной, при условии, что начальное состояние системы находится в соответствующей точке. Каждая условно-оптимальная стратегия оценивается значением функции F:

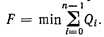
По нему можно выбрать начальное состояние системы и в зависимости от него окончательно определить оптимальную стратегию, т. е., пройдя процесс уже от начала к концу, установить на каждом этапе оптимальные решения.

Принцип оптимальности Беллмана в этой интерпретации задач и динамического программирования означает следующее: оптимальный путь из любой точки, отражающей состояние системы в какой-либо момент времени, не зависит от траектории, ведущей в эту точку. Поэтому для определения оптимального решения в целом необходимо всегда находить оптимальное продолжение процесса относительно состояния, достигнутого в результате решения на предшествующем этапе.

Математическая постановка задачи выглядит следующим образом.

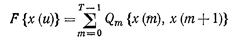
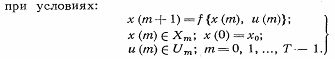
В качестве примера реализации методики динамического программирования можно привести решение задачи по оптимизации режима ведения поезда на одном из участков (рис. 18.2.).

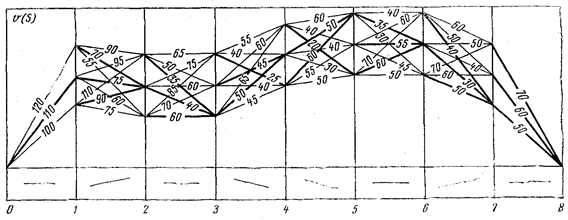
Рис. 18.2 Определение наивыгоднейшего режима ведения поезда по участку

Дата добавления: 2014-01-05