Методы оптимизации

Анализ численных результатов и их применение.

На этом этапе прежде всего решается важнейший вопрос о правильности и полноте результатов моделирования и применимости их как в практической деятельности, так и в целях усовершенствования модели. Поэтому в первую очередь должна быть проведена проверка адек­ватности модели по тем свойствам, которые выбраны в качестве существенных.

Перечисленные этапы моде­лирования находятся в тесной взаимосвязи, в частности, мо­гут иметь место возвратные связи этапов. Так, на этапе по­строения модели может выясниться, что постановка задачи или противоречива, или приводит к слишком сложной ма­тематической модели; в этом случае исходная постановка задачи должна быть скорректирована. Наиболее часто необ­ходимость возврата к предшествующим этапам моделирова­ния возникает на этапе подготовки исходной информации. Если необходимая информация отсутствует или затраты на ее подготовку слишком велики, приходится возвращаться к этапам постановки задачи и ее формализации, чтобы при­способиться к доступной исследователю информации.

Недостатки, которые не удается исправить на тех или иных этапах моделирования, устраняются в по­следующих циклах. Однако результаты каждого цикла име­ют и вполне самостоятельное значение. Начав исследование с построения простой модели, можно получить полезные ре­зультаты, а затем перейти к созданию более сложной и более совершенной модели, включающей в себя новые условия и более точные математические зависимости.

В настоящее время экономист, менеджер может использовать при принятии решения различные компьютерные и математические средства. В памяти компьютеров может содержаться масса информации, организованная с помощью баз данных и других программных продуктов, позволяющих оперативно ею пользоваться. Экономико-математические и эконометрические модели позволяют просчитывать последствия тех или иных решений, прогнозировать развитие событий.

Сформулируем основные понятия, используемые в задачах оптимизации:

Управляемые переменные x₁, x₂,…, x_n – переменные, значения которых можно выбирать в определенных допустимых пределах;

ЛПР (лицо принимающее решение) – человек или группа людей, которые занимаются анализом и выбором значений управляемых переменных, обеспечивающих оптимальное решение;

Эффективное решение – набор значений управляемых переменных, который по некоторым соображениям ЛПР считает наиболее предпочтительными среди всех возможных решений;

Целевая функция задачи оптимизации – количественная мера оптимальности процесса;

Ограничения задачи оптимизации – совокупность условий (равенств, неравенств и т.п.), связывающих характеристики процесса и ограничивающих область изменения управляемых переменных;

Неуправляемые параметры – неизменяемые параметры процесса, значения которых известны;

Случайные факторы – факторы процесса, для которых ввиду их случайности неизвестны точные значения, но известен закон распределения вероятностей этих значений;

Неопределенные факторы – это факторы процесса, значения которых неизвестны;

Математическая модель оптимизации процесса – целевая функция и совокупность ограничений, зависящие от значений управляемых переменных, неуправляемых параметров, случайных и неопределенных факторов;

Допустимое решение – набор значений управляемых переменных, который удовлетворяет одновременно всем ограничениям задачи оптимизации;

Оптимальное решение - набор значений управляемых переменных, который не только удовлетворяет одновременно всем ограничениям задачи оптимизации, но и дает экстремальное значение целевой функции.

В зависимости от вида целевой функции, ограничений и присутствия случайных и неопределенных факторов оптимизационные модели можно в общем случае разделить на следующие классы:

· задачи математического программирования;

· задачи параметрического программирования;

· задачи стохастического программирования;

· оптимизационные задачи массового облуживания;

· задачи статистических игр.

Можно выделить несколько основных типов оптимизационных задач:

· задачи управления запасами;

· задачи распределения ресурсов;

· задачи ремонта и замены оборудования;

· сетевые оптимизационные задачи;

· задачи составления оптимальных расписаний;

· задачи оптимизации систем обслуживания;

· комбинированные задачи, объединяющие в себе черты задач разных типов.

Наиболее часто используются оптимизационные модели принятия решений. Их общий вид таков:

F (X) → max (min)

X Є A

Здесь Х - параметр, который менеджер может выбирать (управляющий параметр). Он может иметь различную природу - число, вектор, множество и т.п. Цель менеджера - максимизировать (минимизировать) целевую функцию F (X), выбрав соответствующий Х. При этом он должен учитывать ограничения X Є A на возможные значения управляющего параметра Х - он должен лежать в множестве А. Приведем основные виды оптимизационных задач менеджмента.

Линейное программирование (ЛП)

Среди оптимизационных задач менеджмента наиболее известны задачи линейного программирования, в которых максимизируемая (минимизируемая) функция F (X) является линейной, а ограничения А задаются линейными неравенствами.

Линейное программирование как научно-практическая дисциплина. Из всех задач оптимизации задачи линейного программирования выделяются тем, что в них ограничения - системы линейных неравенств или равенств. Ограничения задают выпуклые линейные многогранники в конечном линейном пространстве. Целевые функции также линейны. То есть:

· показатель оптимальности L(X) представляет собой линейную функцию от элементов решения ;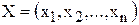

· ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.

Дата добавления: 2014-01-05