Продуктивные модели Леонтьева

Матрица , все элементы которой неотрицательны, является продуктивной, если для любого вектора 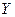с неотрицательными компонентами существует решение уравнения (15) – вектор 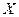, все элементы которого неотрицательны. В таком случае и модель Леонтьева называется продуктивной.

Существует несколько критериев продуктивности матрицы . Согласно одному из них матрица продуктивна, если максимум сумм элементов ее столбцов не больше единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица продуктивна, если 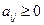для любых 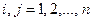и , и 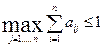существует 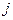такой, что .

Перепишем уравнение (15) с использование единичной матрицы 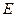в виде:

(16)

Для продуктивных матриц существует обратная матрица 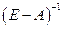, т.е. существует единственное решение уравнения (16):

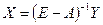(17)

Матрица 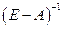называется матрицей полных затрат.

Пример. Данные баланса трех отраслей промышленности за некоторый период времени представлены в таблице. Найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 50, 70 и 20 условных денежных единиц.

N п/п	Отрасль	Потребление	Конечный продукт	Валовой выпуск
	Добыча и переработка углеводородов
	Электроэнергия
	Машиностроение

Решение. Выпишем векторы валового выпуска и конечного потребления и матрицу коэффициентов прямых затрат. Согласно формулам (12) и (14) имеем:

,

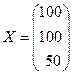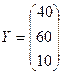
Элементы матрицы равны , то есть

Матрица прямых затрат имеет неотрицательные элементы и удовлетворяет критерию продуктивности:

В случае заданного увеличения конечного потребления новый вектор конечного продукта будет иметь вид:

.

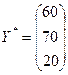Требуется найти новый вектор валового выпуска 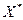, удовлетворяющий соотношениям баланса в предположении, что матрица не изменяется. В таком случае компоненты неизвестного вектора 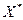находятся из системы уравнений, которая согласно (13) будет иметь вид:

В матричной форме эта система выглядит следующим образом: или 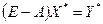, где матрица имеет вид:

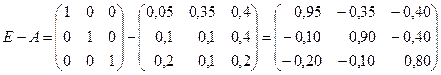
Новый вектор 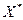рассчитывается как решение этого уравнения баланса:

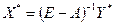
Найдем обратную матрицу (матрицу полных затрат) 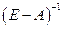. Определитель этой матрицы , значит обратная матрица и решение указанной системы уравнений существуют. Вычисление обратной матрицы дает с точностью до третьего знака:

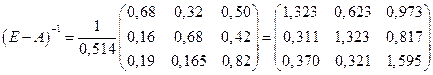
Заметим, что найденная матрица удовлетворяет второму критерию продуктивности матрицы .

Вычислим вектор валового выпуска :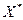

Таким образом, для того чтобы обеспечить заданное увеличение компонент вектора конечного продукта, необходимо увеличить соответствующие валовые выпуски: добычу и переработку углеводородов на 29,2%, производство электроэнергии – 24,5% и выпуск машиностроения – на 45,8% по сравнению с исходными величинами.

Дата добавления: 2014-01-05