
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Диагональная форма матрицы оператора
|
|
|
|
Наиболее простой вид матрица  линейного оператора
линейного оператора 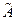 имеет, когда базисом является система ее собственных векторов, т.е. все
имеет, когда базисом является система ее собственных векторов, т.е. все 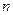 ее собственных
ее собственных  значений различны. В этом случае
значений различны. В этом случае 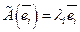 ,
,  при
при 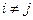 и
и 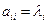 , т.е. матрица
, т.е. матрица  является диагональной:
является диагональной:
 .
.
Следовательно, для того чтобы привести матрицу  оператора
оператора 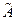 к диагональному виду согласно формуле
к диагональному виду согласно формуле 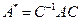 , в качестве матрицы
, в качестве матрицы 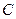 нужно взять матрицу, столбцами которой должны быть собственные векторы оператора
нужно взять матрицу, столбцами которой должны быть собственные векторы оператора 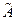 .
.
Пример. Привести к диагональному виду матрицу  .
.
Решение. Характеристическое уравнение этой матрицы имеет вид:

 , откуда
, откуда 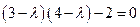 ,
,  ,
,  .
.
Найдем собственные векторы, подставляя найденные собственные значения в матричное уравнение  . Для
. Для  получаем
получаем
 ,
,
отсюда 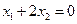 . Полагая
. Полагая 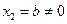 произвольной константой, получаем собственный вектор
произвольной константой, получаем собственный вектор  . Подстановка второго собственного значения
. Подстановка второго собственного значения  приводит к уравнению
приводит к уравнению
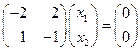 ,
,
Откуда 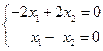 , полагая
, полагая 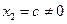 получаем второй собственный вектор матрицы
получаем второй собственный вектор матрицы  :
:  . Поскольку
. Поскольку 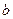 и
и 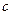 - произвольные числа, одному собственному значению может соответствовать несколько собственных векторов разной длины.
- произвольные числа, одному собственному значению может соответствовать несколько собственных векторов разной длины.
Поскольку собственные значения этой матрицы  , подобная ей диагональная матрица имеет вид:
, подобная ей диагональная матрица имеет вид:
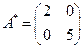
Проверим это по формуле 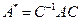 . Составим матрицу
. Составим матрицу 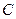 , столбцами которой являются собственные векторы:
, столбцами которой являются собственные векторы:
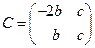 .
.
Найдем определитель матрицы  , а обратная матрица
, а обратная матрица 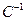 имеет вид:
имеет вид:

По формуле 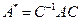 получаем:
получаем:
 .
.
4.6. Квадратичные формы.
4.6.1. Основные сведения о квадратичных формах.
Определение. Квадратичной формой 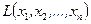 от
от 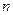 переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
 (50)
(50)
Предполагаем, что коэффициенты квадратичной формы 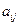 - действительные числа, причем
- действительные числа, причем  .
.
Будем называть симметрическую матрицу
 (51)
(51)
матрицей квадратичной формы (50). Квадратичная форма (50) может быть представлена в матричной форме:
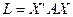 (52)
(52)
где 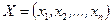 и
и  - вектор-строка и вектор-столбец переменных.
- вектор-строка и вектор-столбец переменных.
В самом деле

 .
.
Пример. Дана квадратичная форма  . Записать ее в матричном виде.
. Записать ее в матричном виде.
Решение. Матрица этой квадратичной формы имеет следующий вид: на главной диагонали стоят коэффициенты при квадратах переменных, а симметричные относительно нее недиагональные элементы равны половинам соответствующих коэффициентов перекрестных произведений переменных данной квадратичной формы. Следовательно:

4.6.2. Преобразование квадратичных форм.
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть векторы-столбцы переменных 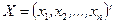 и
и 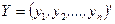 связаны линейным соотношением
связаны линейным соотношением
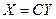
где  ,
,  есть некоторая невырожденная матрица
есть некоторая невырожденная матрица 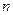 -го порядка. Тогда квадратичная форма
-го порядка. Тогда квадратичная форма
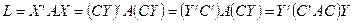 .
.
Итак, при невырожденном линейном преобразовании 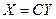 матрица квадратичной формы принимает вид
матрица квадратичной формы принимает вид
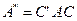 (53)
(53)
Пример. Для квадратичной формы предыдущего примера найти квадратичную форму, полученную из данной линейным преобразованием  ,
,  ,
,  .
.
Решение. Матрица данного линейного преобразования имеет вид:
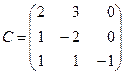 .
.
Применяя формулу (53) к матрице  из предыдущего примера получаем:
из предыдущего примера получаем:
 ,
,
т.е. квадратичная форма принимает вид:
 .
.
4.6.3. Канонический и нормальный виды квадратичной формы.
Определение. Квадратичная форма  называется канонической или имеет канонический вид, если все ее коэффициенты
называется канонической или имеет канонический вид, если все ее коэффициенты  при
при 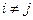 :
:
 (54)
(54)
т.е. матрица является диагональной.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Определение. Квадратичная форма с действительными коэффициентами имеет нормальный вид, если в ее каноническом виде все коэффициенты равны 1 или -1.
Существуют различные методы приведения квадратичной формы к каноническому виду. Рассмотрим один из них
Метод Лагранжа. Заключается в выделении полных квадратов: сначала формируется полный квадрат из слагаемых, содержащих  , затем из слагаемых, содержащих
, затем из слагаемых, содержащих  и т.д. Рассмотрим это на конкретном примере.
и т.д. Рассмотрим это на конкретном примере.
Пример. Привести к каноническому и нормальному виду квадратичную форму
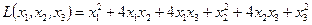
Решение. Применяя метод Лагранжа, получаем:
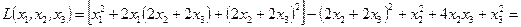



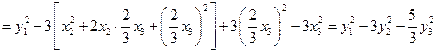 .
.
где  ,
, 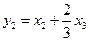 ,
, 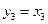 . При приведении к нормальному виду в этой квадратичной форме нужно использовать замену переменных
. При приведении к нормальному виду в этой квадратичной форме нужно использовать замену переменных 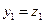 ,
, 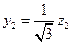 ,
,  . Тогда получаем:
. Тогда получаем:
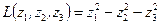
Теорема. (Закон инерции квадратичных форм). При любом способе приведения квадратичной формы (50) с действительными коэффициентами к нормальному виду число квадратов с коэффициентами 1 получается одно и то же, как и число квадратов с коэффициентами -1.
4.6.4. Критерий знакоопределенности квадратичной формы.
Определение. Квадратичная форма (50) называется положительно определенной (отрицательно определенной), если для любых значений переменных 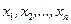 , не равных одновременно нулю, указанная форма имеет положительные (отрицательные) значения.
, не равных одновременно нулю, указанная форма имеет положительные (отрицательные) значения.
Оба этих случая объединены под названием знакоопределенных форм. Если квадратичная форма (50) как положительные, так и отрицательные значения, то она называется знакопеременной.
Квадратичная форма  от
от 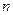 переменных является положительно определенной, тогда и только тогда, если ее нормальный вид содержит ровно
переменных является положительно определенной, тогда и только тогда, если ее нормальный вид содержит ровно 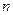 квадратов, т.е. имеет вид
квадратов, т.е. имеет вид 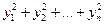 . Понятно, что все
. Понятно, что все 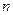 собственных значений матрицы квадратичной формы должны быть положительными.
собственных значений матрицы квадратичной формы должны быть положительными.
Аналогично в нормальный вид отрицательно определенной все 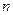 квадратов должны входить со знаком минус, т.е. все
квадратов должны входить со знаком минус, т.е. все 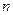 собственных значений матрицы квадратичной формы должны быть отрицательными.
собственных значений матрицы квадратичной формы должны быть отрицательными.
Миноры
 ,
,  ,
,  ,…,
,…,  (55)
(55)
называются главными минорами матрицы  квадратичной формы (50).
квадратичной формы (50).
Теорема. (критерий Сильвестра). Для того чтобы квадратичная форма (50) была положительно определенной, необходимо и достаточно, чтобы были выполнены условия
 (56)
(56)
Для того, чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки главных миноров 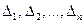 чередовались, причем
чередовались, причем  .
.
Пример. Найти по критерию Сильвестра знакоопределенность квадратичной формы 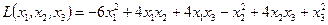 .
.
Решение. Матрица этой квадратичной формы имеет вид:
 .
.
Последовательно вычисляем ее миноры
 ,
,  ,
, 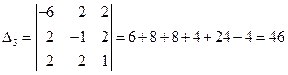 .
.
Поскольку критерий Сильвестра не соблюден, то данная квадратичная форма является знакопеременной.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 13402; Нарушение авторских прав?; Мы поможем в написании вашей работы!