Линейная модель торговли

Одним из примеров экономического процесса, приводящего к понятию собственного числа и собственного вектора матрицы, является процесс взаимных закупок товаров.

Будем полагать, что бюджеты 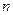стран, которые мы обозначим соответственно , расходуются на покупку товаров. Будем рассматривать линейную модель обмена, или, как ее еще называют, модель международной торговли.

Пусть 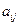- доля бюджета , которую 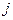-ая страна тратит на закупку товаров у 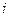-ой страны. Введем матрицу коэффициентов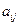

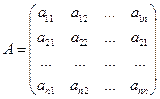(57)

Тогда, если весь бюджет расходуется только на закупки внутри страны и вне ее (это можно трактовать как торговый бюджет), то справедливо условие

(58)

Матрица (57) со свойством (58), в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли.

Для 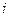-ой страны общая выручка от внутренней и внешней торговли выражается формулой

.

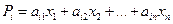Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е. или

, (59)

Если считать, что , , то получаем систему неравенств

(60)

Покажем, что в условиях (59) не может быть знака неравенства. Действительно, сложим все неравенства системы (60). Группируя слагаемые с величинами бюджетов , получаем

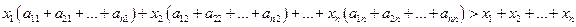
Учитывая (58), выражения в скобках равны единице, следовательно, мы приходим к противоречивому неравенству

,

откуда очевиден только знак равенства.

Таким образом, неравенства (60) принимают знак равенства

(61)

С экономической точке зрения это понятно, так как все страны не могут одновременно получать прибыль.

Введя вектор бюджетов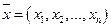(каждая компонента этого вектора характеризует бюджет соответствующей страны). Тогда систему уравнений (61) можно записать в матричной форме

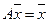, (62)

Уравнение (62) означает, что собственный вектор структурной матрицы , отвечающий ее собственному значению , состоит из бюджетов стран бездефицитной международной торговли.

Перепишем уравнение (62) в виде, позволяющим определять 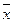и решать соответствующие задачи

Пример. Структурная матрица торговли четырех стран имеет вид

.

Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов задана:

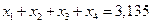(усл. ден. ед.)

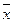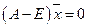Решение. Находим собственный вектор , отвечающий собственному значению заданной структурной матрицы , т.е. решив уравнение , которое в нашем случае имеет вид

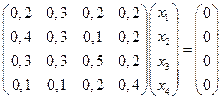
Найдем ранг этой системы, для этого преобразуем матрицу к ступенчатому виду:

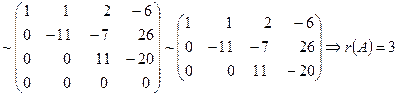
Поскольку ранг этой системы равен трем, то имеем три основных переменных 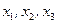и одну свободную - . Выразим основные переменные 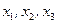через свободную :

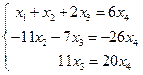
Из последнего уравнения системы находим , далее найденное значение подставляет во второе уравнение системы:

, , ,

Из первого уравнения системы, учитывая найденные значения и , найдем значение :

,

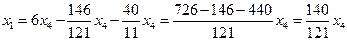Итак, 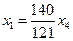, , . Пусть , тогда , , .

Подставив найденные значения в заданную сумму бюджетов, найдем величину :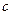

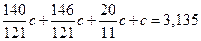
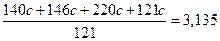
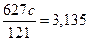
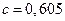, откуда окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в условных денежных единицах):

, , , .

Дата добавления: 2014-01-05