Тема 1. Равновесие жидкости

Основные понятия: дифференциальное уравнение равновесия жидкости; три формы записи основного уравнения гидростатики; поверхность равного давления; закон Паскаля; абсолютное, манометрическое и вакуумметрическое давление; сила давления на плоские и криволинейные поверхности; относительный покой жидкости; закон Архимеда; относительный покой жидкости.

Вопросы, на которые необходимо найти ответ в ходе изучения темы:

1. Что обозначает выражение?
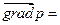
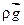2. Какие выводы можно сделать, если ?
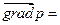
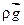3. Как можно получить основное уравнение гидростатики в дифференциальной форме?
4. В каком случае уравнение Бернулли превращается в основное уравнение гидростатики?
5. Запишите основное уравнение гидростатики в трех его формах. Объясните значение каждого входящего в него слагаемого.
6. Какая плоскость называется плоскостью равного давления?
7. В чем разница между напором и давлением?
8. Что называют удельной энергией положения?
9. Объясните закон Паскаля.
10. Какие механизмы действуют на основе закона Паскаля?
11. Что называют абсолютным давлением, манометрическим давлением, вакуумом?
12. Какое давление будет в напорном потоке, если пьезометрическая линия проходит ниже его геометрической оси?
13. Как определить давление в любой точке жидкости, находящейся в закрытом резервуаре? От чего оно зависит?
14. Чему равна результирующая сила давления на стенки резервуара произвольной формы? Как это доказать?
15. Как определить силу давления жидкости на плоскую горизонтальную поверхность?
16. В чем заключается гидростатический парадокс?
17. Как определить силу давления жидкости на плоскую вертикальную поверхность?
18. Как определить точку приложения результирующей силы давления на плоскую вертикальную поверхность?
19. Как определяется величина силы давления на криволинейные поверхности?
20. Как рассчитать допустимое давление в трубе, чтобы не допустить ее разрыва?
21. Сформулируйте закон Архимеда.
22. Какова природа действия Архимедовой силы?
23. Каковы условия плавания тел, их равновесия?
24. Объясните принцип действия ареометра (прибора для измерения плотности жидкости).
25. Что такое относительный покой жидкости?
26. Какие силы действуют при относительном покое жидкости? Как их записать?
27. Как определить положение свободной поверхности жидкости при ее вращении в цилиндрическом сосуде?
28. Как распределяется давление в любой фиксированной круглоцилиндрической поверхности при относительном покое жидкости?

Практические задачи, решение которых может быть найдено после изучения теоретического материала:

Задача 2.1-1

В сообщающихся сосудах находятся вода и масло. Определить плотность масла, если высота столба воды Н = 150 мм, а разность уровней жидкости в сосудах d = ___мм.

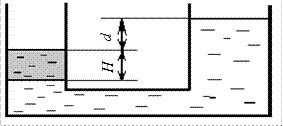
Рис. 2.1. К задаче 2.1-1

Задача 2.1-2

Для измерения высоты налива мазута установлена вертикальная труба. В трубу с малой скоростью подают воздух. Определить высоту Н налива мазута удельным весом g = 8700 Н/м³, если давление воздуха, поступающего в резервуар, эквивалентно высоте ртути в ртутном манометре h _рт = d _н мм (r_рт = 13600 кг/м³). Трением при движении воздуха пренебречь.

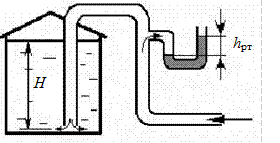
Рис. 2.2. К задаче 2.1-2

Задача 2.1-3

Для повышения гидростатического давления применяется мультипликатор давления, давление на входе которого 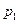= 20 кПа, а диаметры поршней d = d _н мм и D = 400 мм. Определить давление жидкости 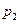на выходе из мультипликатора.

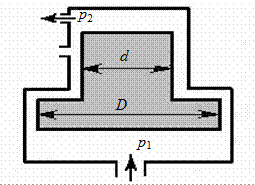
Рис. 2.3. К задаче 2.1-3

Задача 2.1-4

Два сообщающихся цилиндра наполнены жидкостью. В меньший цилиндр диаметром d = d _н мм заключен поршень весом G = 100 Н. На какой высоте H установится уровень жидкости в большом цилиндре, диаметром D = 800 мм, когда вся система придет в равновесие? Удельный вес жидкости γ = 9,81 кН/м³. Трением пренебречь.

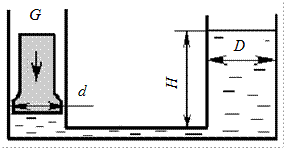
Рис. 2.4. К задаче 2.1-4

Задача 2.1-5

Диаметры поршней дифференциального предохранительного клапана равны D = 2 d _н мм и d = d _н мм. Пренебрегая весом поршней и силой трения, определить давление, при котором клапан откроется, еслижесткость пружины с = 50 Н/мм, а ее предварительный натяг: x ₀ = 12 мм.

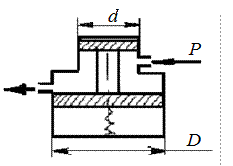
Рис. 2.5. К задаче 2.1-5

Примечание. Сила пружины F = с x ₀

Задача 2.1-6

Плотность жидкости определяется погружением в нее поплавка. Вес поплавка в воздухе равняется 0,72 кН. Вес поплавка, погруженного в испытуемую жидкость G ₁ = 0,54 кН, вес поплавка, погруженного в воду G ₂ = 0,56 кН. Определить плотность жидкости.

Задача 2.1-7

Бак водонапорной башни сварен из стальных полос высотой. Определить необходимую толщину стенки нижней полосы, если допускаемое напряжение на разрыв [s] = 1×10⁸ Па, диаметр бака D = 100 d _н м, глубина воды в баке Н = 10 м.

Задача 2.1-8

Круглое отверстие в дне резервуара с жидкостью закрыто пластмассовым шариком, вес которого G = 2,45 Н и радиус r = 0,1 м. Диаметр отверстия d = d _н мм. Определить давление р, действующее на шар снизу, при котором отверстие откроется, если глубина воды Н = 2 м.

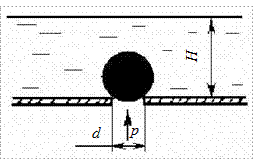
Рис. 2.6. К задаче 2.1-8

Задача 2.1-9

Плотность жидкости измеряется при помощи ареометра. Размеры аэрометра: d = d _н мм, D = 1,5 d _н мм, Н = 100 мм, h = 50 мм, масса m = 0,054 кг. Определить плотность жидкости.

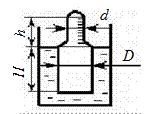
Рис. 2.7. К задаче 2.1-9

Задача 2.1-10

Определить абсолютное давление на поверхности жидкости в сосуде и высоту h, если атмосферное давление равняется 740 мм.рт.ст. Поддерживающая сила F = 10 H, вес сосуда G = 2 Н, его диаметр d = d _н мм. Толщиной стенки сосуда пренебречь.

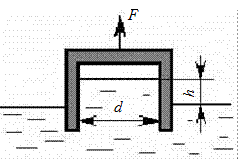
Рис. 2.8. К задаче 2.1-10

2.1.1. Дифференциальное уравнение равновесия жидкости.
Поверхность равного давления

Предположим, что в точке М находится объем жидкости dV (см. рис. 2.9). На него воздействуют силы давления соседних объемов. Определим результирующую силу давления на объем dV. dV расположен параллельно осям координат, da, db, dc – его стороны. В точке М давление обозначим как p. В точках 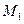и 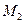, принадлежащих сторонам параллельным плоскости x0y давление будет соответственно 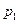и 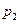. Если рассматривать одну из сторон параллелепипеда, то результирующая сила давления на эту сторону действует по нормали к ней и ориентирована внутрь объема dV.

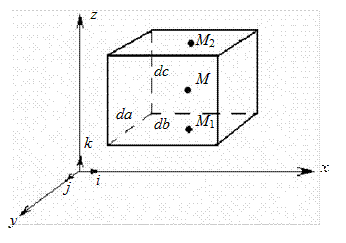
Рис. 2.9. Объем жидкости, находящийся в равновесии

Для результирующей силы сторон объема dV, параллельных плоскости x0y можно записать

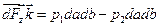или ,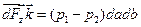

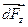параллельна оси 0z.

Разность 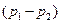можно записать в виде 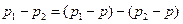, но в соответствии со свойством градиента давления можно написать

, ,

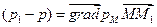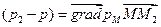откуда .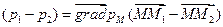

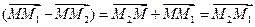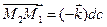Так как и , то

.

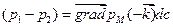Таким образом, результирующая сила 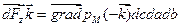, но dcdadb = dV, oткуда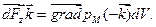

Аналогичные результаты мы получим для сил 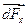и .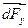

Результирующая всех сил, действующих на объем dV будет соответственно

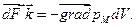
(2.1)

Выводы:

1. Результирующая сила 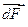направлена в противоположную сторону, чем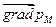

2. 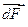перпендикулярна плоскости, проходящей через точку М, на которой давления одинаковы и ориентирована в сторону уменьшения давления.

В жидкости, находящейся в покое, действуют:

– сила тяжести

,

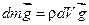направленная вертикально вниз;

– равнодействующая сила давления

,

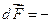
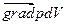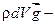
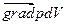= 0

или .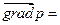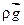

(2.2)

Выводы:

1. Вектор градиента давления направлен вертикально вниз, как и вектор .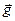

2. В жидкости, находящейся в равновесии давление увеличивается сверху вниз.

3. В покоящейся жидкости плоскости равного давления горизонтальны.

4. В покоящейся жидкости давление в точке зависит только от ординаты z.

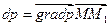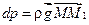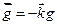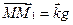Т.к. , то с учетом полученного уравнения, можно записать . Т.к. и , то

.

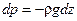(2.3)

Нами получено основное уравнение гидростатики в дифференциальной форме.

Дата добавления: 2014-01-05