Деформации. Тензор деформаций

Под действием внешних нагрузок происходит деформация, в результате которой могут изменяться форма и размеры тела. Деформации, исчезающие после снятия напряжений, называют упругими, а сохраняющиеся после прекращения действия внешних напряжений – остаточными. Остаточная деформация, происходящая без разрушения, называется пластической.

По результатам механических испытаний оценивают различные характеристики упругости, а чаще остаточной деформации. Наиболее широко используют следующие характеристики деформации: удлинение (укорочение), сдвиг и сужение (уширение) образцов.

Увеличение длины образца в результате деформации обычно характеризуют относительным удлинением δ, %

где l₀ и l_k начальная и конечные длинны; Δl – абсолютное удлинение.

Величина δ является условной характеристикой, поскольку деформация с самого начала развивается на непрерывно изменяющейся длине l и отношение Δl/l₀ лишено физического смысла.

Допустим образец длиной l₀ = 10 мм удлинится на 1 мм, а затем с l₁ = 11 мм до l₂ = 12 мм, тогда в первом случае

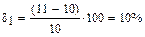
а во втором при том же Δl = 1 мм величина

Очевидно, суммарное истинное удлинение (1/10 + 1/11 + …)*100% меньше условного. Это истинное относительное удлинение

Разница между δ и e растет с увеличением степени деформации. При δ = 25% е = ln1.25 = 22%, а при δ = 100% е = ln2 = 69%. В области малых деформаций δ ≈ е.

В отличие от условного, истинное относительное удлинение аддитивно. Действительно, в рассмотренном выше примере суммарное истинное удлинение по достижении l₂ равно

Удлинение и укорочение образца обычно происходят под действием нормальных напряжений. Касательные напряжения вызывают сдвиговые деформации, которые оценивают по углу сдвига α (в радианах) или по величине относительного сдвига g = tgα.

Относительные удлинения и сдвиги (e и g) – фундаментальные характеристики деформации, которые используются в теориях упругости и пластичности. Совокупность удлинений и сдвигов – тензор деформации – по аналогии с тензором напряжений характеризует любое деформированное состояние в данной точке и позволяет определять е в любом направлении и g в любой плоскости.

В общем случае тензор деформации характеризуется девятью компонентами – тремя удлинениями и шестью сдвигами:

из которых только шесть независимых, так как g_xy = g_yx, g_yz = g_zy, g_zx = g_xz.

В случае если три главных направления деформации (в которых сдвиги равны нулю) заранее известны и их можно совместить с координатными осями, тензор деформации характеризуется совокупностью трех главных удлинений

где е₁ и е₃ – наибольшее и наименьшее удлинение.

Зная тензор деформации в данной точке тела, можно оценить относительную деформацию в любом направлении, исходящем из этой точки. Например, удлинение в направлении, которое характеризуется направляющими косинусами a_x, a_y, a_z рассчитывается как

Максимальные сдвиги происходят в направлениях, делящих пополам углы между направлениями главных удлинений:

g₁ = e₁ –e_3, g₂ = e₁ – e₂, g₃ = e₂ – e₃.

Эти три максимальных сдвига называют главными сдвигами.

Третей широко используемой характеристикой деформации является относительное сужение φ, %:

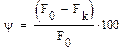
где F₀ и F_k – начальная и конечная площади поперечного сечения образца.

Как и δ, это условная характеристика деформации, ибо площадь сечения непрерывно меняется в процессе испытания. Истинное относительное сужение можно рассчитать как

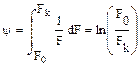
Между е, δ и ψ существует функциональная связь в области равномерной деформации, т.е. пока величина относительных изменений размеров во всех точках рабочей части образца одинакова. Эта связь следует из условия постоянства объема при пластической деформации:

F₀l₀ = F_kl_k или l_k/l₀ = F₀/F_k.

Относительное сужение

следовательно

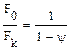
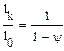
Отсюда

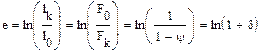
Еще одним важным следствием постоянства объема при пластической деформации является равенство нулю суммы трех главных удлинений. Относительное изменение объема при деформации куба со стороной, равной единице, равно

Если объем при деформации не меняется, то

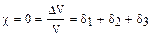
Почленно интегрируя, получим

Помимо описанных характеристик деформации, используют и другие, более частные. Например, величину деформации при испытании на изгиб можно оценивать по стреле прогиба, а на кручение – по углу скручивания и т.д.

3. СХЕМЫ НАПРЯЖЕННОГО СОСТОЯНИЯ ПРИ МЕХАНИЧЕСКИХ ИСПЫТАНИЯХ РАЗЛИЧНЫХ ВИДОВ

Результаты механических испытаний в значительной мере определяются схемой напряженного состояния, ко­торая задается в образце условиями его нагружения. Один и тот же материал может проявлять резко различ­ные характеристики прочности и пластичности, если его испытывать при разных схемах напряженного состоя­ния. Всего таких схем существует восемь. Они приведе­ны в табл. 1 вместе с соответствующими тензорами на­пряжений и примерами реализации в различных испы­таниях и условиях эксплуатации.

Приведенные в табл. 1 схемы применимы, строго го­воря, лишь в области упругой и равномерной деформа­ции. В процессе реальных испытаний, особенно после на­чала сосредоточенной пластической деформации, эти схемы могут значительно измениться.

Схемы напряженных состояний (по Я.Б. Фридману) Таблица 1

Напряженное состояние	Схема НС	Тензор напряжений	Примеры реализации
Линейные	Одноосное растяжение
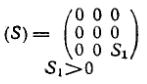
Одноосное сжатие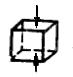
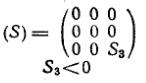
Плоские	Двухосное растяжение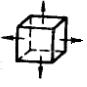
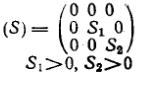
Двухосное сжатие

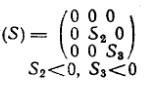
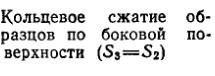
Схема напряженного состояния влияет на механичес­кие свойства и особенно на характеристики деформации (пластичности) через соотношение сжимающих и растя­гивающих напряжений. Сжимающие напряжения в боль­шей мере способствуют проявлению пластичности, чем растягивающие (в условиях гидростатического сжатия разрушения вообще не происходит). Поэтому чем боль­ше роль сжимающих напряжений в схеме напряженного

состояния, тем она считается «мягче», так как при ее ре­ализации деформационная способность материала больше.

Для количественной оценки «мягкости» схемы на­пряженного состояния Я.Б. Фридман предложил рассчи­тывать специальный коэффициент мягкости

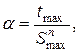(13)

где 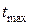— максимальное касательное напряжение — см. формулу (6);

Sⁿ_max— наибольшее приведенное главное нормальное напряжение.

Продолжение таблицы 1

Напряженное состояние	Схема НС	Тензор напряжений	Примеры реализации
Плоские	Разноименное плоское нап-ряженное со-стояние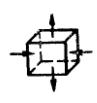
Объемные	Трехосное растяжение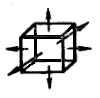
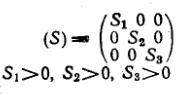
Трехосное сжатие
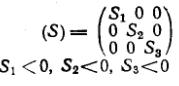
Разноименное объемное напряженное состояние

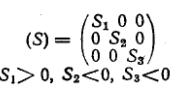
По второй теории прочности

где 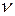— коэффициент Пуассона.

Тогда (14)

У многих металлов коэффициент Пуассона примерно одинаков — ν~0.25, и формулу 14 можно упростить.

Смысл того, почему отношение t_max/ Sⁿ_max должно характеризовать «мягкость» схемы напряженно­го состояния, сводится к следующему. Величина t_max оп­ределяет легкость начала пластической деформации, а Sⁿ_max — хрупкого отрыва. ЕСЛИ t_max > Sⁿ_max, то при нагружении образца, прежде чем произойдет хрупкое раз­рушение, начнется пластическая деформация и хрупкий отрыв будет предотвращен. Если же t_max < Sⁿ_max, то разрушение может произойти до появления пластичес­кой деформации. Поэтому чем больше t_max и меньше Sⁿ_max (т. е. больше α), тем более благоприятны условия для развития пластической деформации.

В то же время, как следует из формулы (14), величина α определяется соотношением сжимающих и растя­гивающих напряжений. В табл. 2 приведены значения коэффициента мягкости для испытаний нескольких ви­дов с различными схемами напряженного состояния.

Коэффициент мягкости α при испытаниях различных видов Таблица 2

Вид испытания	Главные нормальные напряжения	α
S1	S2	S3
Трехосное растяжение	S	S	S
Одноосное растяжение	S			0.5
Кручение	S		-S	0.8
Одноосное сжатие			-S
Трехосное сжатие	-S	(-7/3)·S	(-7/3)·S

В условиях трехосного растяжения, когда сжимаю­щих напряжений в схеме напряженного состояния нет, α=0. Эта схема отличается максимальной «жестко­стью», т. е. способность материала деформироваться в таких условиях минимальна. Наоборот, при гидроста­тическом сжатии материал должен проявить максималь­ную пластичность — здесь α=4. Поэтому некоторые металлы и сплавы, отличающиеся хрупкостью при ма­лых значениях α (например, серый чугун, закаленная сталь, интерметаллиды), могут деформироваться и бе­зопасно служить в условиях более мягких схем напря­женного состояния.

Следует подчеркнуть, что абсолютные значения ко­эффициента мягкости не позволяют количественно оце­нивать характеристики деформации (δ, φ и др). Вели­чина α может и должна использоваться лишь для сра­внительной оценки «мягкости» различных испытаний.

Дата добавления: 2014-01-05