Закон Гука и константы упругих свойств

Поведение металлов при упругой деформации с достаточно хорошим приближением описывается известным законом Гука, который определяет прямую пропорциональность между напря­жением и упругой деформацией. На рис. 1 показаны начальные (упругие) участки кривых напряжение — деформация при одно­осном растяжении, кручении (сдвиге) и гидростатическом сжа­тии. Наклон каждой из этих трех кривых, т. е. коэффициент про­порциональности, связывающий напряжение и деформацию, ха­рактеризует модуль упругости:

E=S/e,

G=t/g,

К=Р/х.

Модуль Е, определяемый при растяжении, называется моду­лем Юнга (нормальной упругости), модуль G — модулем сдвига (касательной упругости) и К — модулем объемной упругости (Р — гидростатическое давление, χ— относительное уменьшение объема). Модули упругости определяют жесткость материала, т.е. интенсивность увеличения напряжения по мере упругой дефор­мации.

Механизм упругой деформации металлов состоит в обратимых смещениях атомов из положения равновесия в кристаллической решетке. Чем больше величина смещения каждого атома, тем больше упругая макродеформация всего образца. Величина этой упругой деформации в металлах не может быть большой (относи­тельное удлинение в упругой области обычно меньше 0,1 %), так как атомы в кристаллической решетке способны упруго смещать­ся лишь на небольшую долю межатомного расстояния. Физичес­кий смысл модулей упругости как раз и состоит в том, что они характеризуют сопротивляемость металлов упругой деформации, т.е. смещению атомов из положений равновесия в решетке. Если сравнивать два металла, например, с разными Е (см. рис. 1, а, прямые 1 и 2), то для примерно одинакового смещения атомов (равной упругой деформации) при большем Е потребуется большее напряжение (прямая 2).

В отсутствие напряжений атомы металлов находятся, точнее колеблются, у неких равновесных положений в узлах кристаллической решетки. Сила (энергия) взаимодействия между двумя со­седними атомами складывается из сил притяжения между поло­жительными ионами и электронами, с одной стороны, и сил отталкивания между ионами за счет деформации их электронных оболочек — с другой. На рис. 2 показана схема распределения сил отталкивания (кривая /) и притяжения (кривая 2) в функции расстояния между атомами. Видно, что при сближении атомов силы отталкивания сначала слабо, а затем — при перекрытии электронных оболочек — резко возрастают. Силы притяжения, естественно, плавно убывают по мере увеличения межатомного расстояния. Результирующая сила (см. рис. 2, кривая 3) становит­ся нулевой на некотором расстоянии а₀, которое соответствует равновесному положению атомов в узлах кристаллической решет­ки.

Рис. 1. Упругие участки кривых напряжение — деформация, при одноосном растяжении (а), кручении (б) и гидростатическом сжатии (в)

Тангенс угла наклона почти прямолинейного участка кривой 3 вблизи а₀ характеризует интенсивность прироста напряжения, необходимого для упругого смещения атомов из положений рав­новесия, т. е. модуль упругости.

Выражения определяют связь между напряжения­ми и деформациями в одном и том же направлении. Однако де­формация может не совпадать по направлению с напряжением. Мы уже знаем, например, что при одноосном растяжении воз­никает трехосная деформация. Тогда описанный эле­ментарный закон Гука должен быть заменен обобщенным, кото­рый устанавливает линейную связь между напряжениями и де­формациями в любых направлениях, т.е. между всеми компонен­тами тензора напряжений и тензора деформаций.

Для изотропного тела

e_x=E^-1[S_x-v(S_y+S_z)],
в_у=E^-1[S_y-v(S_x+S_z)],
e_z = E^-1[S_z-v(S_{x +} S_y)],

g_xy=t_xy/G

g_xz=t_xz /G

g_yz=t_yz/G

где v — коэффициент Пуассона при одноосном растяжении (сжа­тии), характеризующий отношение поперечной относительной деформации к продольной.

Если исходный радиус образца г₀, а длина l₀, то после некоторой деформации они изменятся соответ­ственно до r₁ < r₀ и l₁ > l₀. Тогда

Расстояние между атомами

Рис. 2. Схема распределения сил взаи­модействия между соседними атомами

Отсюда е_y = е_z = — ve_x.

Коэффициент Пуассона v — чет­вертая важнейшая константа упру­гих cвойств после модулей упругос­ти. Эти четыре константы связаны между собой:

E=2G(l+v), E=3K(l -2v).

Зная две из них, можно рассчитать остальные.

Численные значения констант упругости некоторых чистых металлов приведены в табл.

Обобщенный закон Гука для изотропного тела может быть за­писан и в виде уравнений, связывающих напряжения с деформа­циями:

S_x = Kx+2Ge_x,

S_y = Кx+ 2Ge_y,

S_z = Kx+2Ge_z

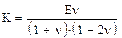
где К и G— постоянные (коэффициенты упругости), x = е_х + е_y + е_z — относительное изменение объема.

Обобщенный закон Гука записывается относительно просто для изотропного тела. Однако металлы имеют кристаллическую структуру и являются телами анизотропными. В частности, их упругие свойства в разных кристаллографических направлениях не одинаковы.

Анизотропия упругих свойств экспериментально просто выяв­ляется при исследовании монокристаллов. Например, модуль нор­мальной упругости монокристаллов меди может колебаться в за­висимости от направления их деформации — от 68 до ~200 ГПа. Для поликристаллических образцов, состоящих из большого чис­ла различно ориентированных зерен, определяемые среднеста­тистические значения упругих констант примерно постоянны и не зависят от направления (у меди, например, E=125 ГПа, см. табл..

Для анизотропного тела обобщенный закон Гука существенно усложняется: он отражает прямую пропорциональность между каждым компонентом тензора деформаций и всеми шестью неза­висимыми компонентами тензора напряжений. Коэффициента­ми пропорциональности в соответствующих уравнениях служат модули упругости. Не менее важными являются уравнения связи компонентов тензора деформации с компонентами тензора на­пряжений. В этих уравнениях используются так называемые коэф­фициенты упругости, связанные определенными соотношения­ми с модулями.

Таблицы модулей и коэффициентов упругости записывают обычно в виде матриц:

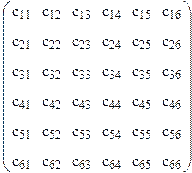
Благодаря симметричности матриц относительно диагонали с₁₁—с₆₆ число независимых модулей (коэффициентов) упругости уменьшается до 21. Следовательно, для расчета всех составляю­щих тензора напряжений надо знать тензор деформаций и 21 модуль упругости анизотропного тела. Константы упругости относятся к категории стабильных свойств, относительно мало меняющихся под влиянием различных факторов. С повышением температуры от 0 К до температуры плавления модули упругости чистых металлов и большинства спла­вов снижаются в 2—2,5 раза. Зависимость эта нелинейна.

Причина уменьшения модулей упругости при нагреве связана с увеличением равновесного межатомного расстояния а₀ из-за тер­мического расширения. Поскольку Е = к/а^m, где к и т — постоян­ные для каждого материала, наблюдается прямая связь (особенно в области невысоких температур) между коэффициентом терми­ческого расширения и температурным коэффициентом модуля Е.

Таблица. Константы упругости чистых поликристаллических металлов при комнатной температуре (А.И. Чижик)

Металл	Е- 10^-5, МПа	G- 10^-5, МПа	К- 10^-5, МПа	V
Железо	2,17	0,89	1,72	0,28
Никель	2,05	0,78	1,87	0,31
Медь	1,25	0,46	1,42	0,34
Алюминий	0,72	0,27	0,75	0,34
Титан	1,08	0,41	1,27	0,34
Кобальт	2,04	0,76	1,87	0,31
Хром	2,40	0,90	1,94	0,30
Молибден	8,47	1,22	2,80	0,30
Цинк	0,94	0,37	0,62	0,29

Модули упругости металлов — структурно малочувствитель­ные свойства. Например, размер зерна почти не влияет на них, а сильная холодная деформация лишь немного (на ~1%) снижает модули, что связывается с влиянием остаточных микронапряжений, возникающих при наклепе. Конечно, если в результате де­формации будет формироваться текстура, то модули могут суще­ственно изменяться из-за увеличившейся анизотропности дефор­мированного металла.

При легировании металлов элементами, образующими твер­дые растворы, модули упругости изменяются по закону, близко­му к линейному, причем могут и увеличиваться, и уменьшаться. Модуль упругости твердых растворов повышается в тех случаях, когда силы связи растворенных атомов и атомов основы больше, чем в чистом металле, и наоборот. Искажения решетки вокруг растворенных атомов способствуют снижению модулей.

Если при легировании образуется вторая фаза с собственным модулем упругости, большим, чем у основы, то в этом случае модуль упругости сплава тоже повышается, как, например, при введении в алюминий малорастворимых добавок марганца, ни­келя, бериллия и др. Однако если вторая фаза мягче мат­рицы, то увеличение ее количества вызывает снижение модулей упругости базового металла. Примером может служить серый чу­гун, у которого модули заметно ниже, чем у чистого железа (у чугуна марки СЧ 28-48 E ~135 ГПа, в то время как у железа E ~ 217 ГПа).

Кстати, серый чугун с графитными включениями является одним из редких примеров сплава, у которого модули упругости зависят от структуры. Это связано с концентрацией напряжений у границ графитных включений и возникновением там местной пластической деформации. По мере увеличения компактности графитные включений этот эффект ослабляется и модули растут. У чугуна с шаровидным графитом E ~175 ГПа.

Сопоставление модулей упругости технически важных метал­лов и многочисленных сплавов на их основе показывает, что в пределах каждой группы сплавов модули различаются слабо. Так, колебания модуля нормальной упругости конструкционных угле­родистых и легированных сталей, существенно отличных по со­ставу, лежат в диапазоне 196 — 224 ГПа, т. е. отличаются не боль­ше чем на 12 %. Увеличение концентрации цинка в латунях от нескольких процентов до 40 % вызывает снижение модуля Е все­го на 5 — 6 %. Серьезные различия в константах упругости наблю­даются лишь в сплавах разных систем. Скажем, модули упругости титановых сплавов почти в 1,5 раза ниже, чем у сталей, и на ~35 % выше, чем у алюминиевых сплавов.

Коэффициент Пуассона слабо отличается даже при сравнении сплавов разных систем, поскольку он близок почти у всех чистых металлов. С повышением температуры v меняется еще слабее модулей упругости, проявляя слабую тенденцию к росту.

Дата добавления: 2014-01-05