Неполная упругость металлов и внутреннее трение

В области упругой деформации, где действует закон Гука, у металлов и сплавов наблюдается ряд отклонений от чисто упру­гого поведения. Некоторые из них известны давно, однако при­рода неполной упругости металлов вскрыта лишь в последние десятилетия.

Одним из известных проявлений неполной упругости метал­лов является эффект Баушингера. Он заключается в том, что при повторном нагружении пластически слабодеформированного об­разца в обратном направлении его сопротивление малым пласти­ческим деформациям снижается. Это снижение может быть дос­таточно заметным. Так, у некоторых сталей и титановых сплавов оно может достигать 15—20 %.

Допустим, мы растянули образец на 1—2% (до точки а на рис. 3). Теперь снимем нагрузку и будем подвергать его сжатию. Кри­вая напряжение — деформация (о 'ес) будет лежать ниже соответ­ствующей кривой (о'b), которую мы получили бы при повторном растяжении.

Если точка b соответствует здесь началу пластической дефор­мации, то отрезок bc = δ_Б представляет так называемую баушингеровскую деформацию, которая является одной из основных количественных характеристик эффекта Баушингера.

Процесс, определяющий этот эффект, состоит в обратном движении дислокаций, порожденных различными источниками при первоначальном растяжении. На начальных стадиях дефор­мации постепенно растущее число генерируемых дислокацион­ных петель движется относительно легко и на значительные рас­стояния вплоть до остановки у каких-либо барьеров. Возникающая дислокационная структура достаточно стабильна и мало ме­няется при разгрузке. Поэтому при повтор­ном растяжении сопротивление деформиро­ванию либо несколько возрастает, либо практически не меняется по сравнению с первоначальным. При изменении же знака напряжения дислокации вынуждены дви­гаться обратно по направлению к источни­кам. В результате перемещение дислокаций начинается при более низких напряжениях и появляется дополнительная баушингеровская деформация.

Рис. 3. Схема эффекта Баушингера

После значительной предварительной пластической деформа­ции (>2—3%) перераспределение дислокаций при обратном на­гружении затрудняется и баушингеровская деформация прибли­жается к нулю.

Особенно большое практическое значение имеет эффект Бау­шингера при эксплуатации и испытаниях в условиях циклическо­го нагружения.

К важным проявлениям неполной упругости металлов отно­сится упругое последействие. Оно свидетельствует о том, что не вся обратимая деформация металла является чисто упругой. Возьмем образец и создадим в нем напряжение в пределах упру­гого участка кривой напряжение — деформация. После разгрузки такой образец будет иметь те же размеры, что и до нагружения. Проследим, как будет изменяться его удлинение во времени под действием приложенного напряжения и после разгрузки. Соот­ветствующая диаграмма представлена на рис. 4. Оказывается, что наш образец деформируется чисто упруго, т.е. с очень большой скоростью лишь на величину ОС, а затем удлиняется медленнее, по закону, близкому к параболическому. После разгрузки в точке К происходит очень быстрое снятие чисто упругой деформации (KM ~ OC), а затем — относительно медленное — остальной де­формации. В конце концов δ = 0 (в точке N), образец имеет исход­ные размеры, но ясно, что далеко не вся обратимая деформация является чисто упругой.

Механизм упругого последействия может быть связан с пере­мещением точечных дефектов, например в металлах с о.ц.к. ре­шеткой — атомов примесей внедрения. До нагружения эти атомы располагаются в междоузлиях, например на середине ребер ку­бической решетки, статистически равномерно (рис. 5, а). Под действием напряжения происходит постепенное перераспределе­ние примесных атомов. Они стремятся занять междоузлия на реб­рах вдоль оси нагружения (см. рис. 5, б), где вызывают наимень­шие искажения решетки. В результате каждая элементарная ячей­ка и весь образец удлиняются вдоль направления действия на­грузки. Причем происходит это не мгновенно. Поскольку переход примесных атомов в новое положение требует диффузионных пере­скоков, он продолжается достаточно длительное время. После разгруз­ки происходит обратное перераспределение примесных атомов, и об­разец принимает исходные размеры (см. рис. 4, участок MN).

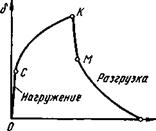Рис. 4. Схема упругого последей­ствия

Более общей причиной упругого последействия считается струк­турная и химическая неоднородность технических металлов и спла­вов. При напряжениях значительно ниже тех, которые вызывают макроскопическую пластическую деформацию металлического образца, в отдельных его зернах начинается локальная (микро­пластическая) деформация, связанная с перемещением дисло­каций. В нашем эксперименте, когда на образец действовало по­стоянное напряжение, после почти мгновенной упругой дефор­мации до точки С (см. рис. 4) удлинение может продолжаться за счет микропластической деформации, постепенно затухая из-за сопротивления упругой среды, окружающей пластически дефор­мирующиеся объемы. После разгрузки упруго продеформирован-ные участки не могут полностью вернуться в исходное состоя­ние, так как этому препятствуют пластически продеформированные области. Под действием остаточных напряжений в этих обла­стях постепенно идет обратная пластическая деформация, кото­рая приближает размеры образца к исходным.

Упругое последействие может в ряде случаев проявляться на практике. Например, из-за него после деформационной правки или после сварки может возникать поводка изделий. Упругое последействие вызывает нежелательное увеличение деформации пружин и мембран, работающих под нагрузкой в точных приборах.

Скорость упругого последействия, а также его величина зави­сят от состава, структуры материала и условий его испытания. Увеличение гетерогенности структуры, неоднородность пласти­ческой деформации, облегчение ее под воздействием различных факторов усиливают эффект упругого последействия. Например, повышение температуры резко увеличивает скорость последействия (в цинке на 50 % при повышении тем­пературы на 15° С). Закалка стали и ее пласти­ческая деформация усиливают склонность к упругому последействию из-за увеличения нео­днородности структуры.

Таким образом, в металлах еще до начала макропластической деформации (на упругом участке кривой напряжение — деформация) возможны неупругие явления, такие, как дви­жение дислокаций, точечных дефектов, пе­ремещение атомов в области границ зерен и т. д. Эти явления, сопровождающиеся местны­ми пластическими деформациями, наблюда­ются при низких напряжениях и имеют важ­ное практическое значение.

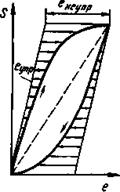
Рис. 6. Образование петли гистерезиса в результате неупругих явлений

Неупругие эффекты служат причинами внутреннего трения, характеризующего необратимые потери энергии внутри металла при механических колебаниях. Линии диаграммы напряжение — деформация при нагрузке и разгрузке из-за неполной упругости металлов не совпадают (рис. 6), а образуют петлю гистерезиса. Ее площадь и характеризует энергию, рассеянную за один цикл нагружения.

Внутреннему трению в последние годы уделяется большое вни­мание. Это связано с большим практическим значением способ­ности металлических материалов к рассеиванию энергии при нагружении в упругой области. Знание величины внутреннего тре­ния необходимо для грамотного выбора материала, работающего в определенных условиях. Например, демпфирующие материалы для разного рода амортизаторов, способные быстро гасить коле­бания, должны обладать высоким внутренним трением. Такие материалы обладают повышенным сопротивлением усталостно­му разрушению при возникновении резонансных колебаний в процессе эксплуатации.

Многие детали измерительных приборов, наоборот, не долж­ны рассеивать упругую энергию, чтобы обеспечить малую инер­ционность и высокую точность измерений. Такие детали должны изготавливаться из материалов с малым внутренним трением. Чистые металлы располагаются в следующий ряд по мере убыва­ния демпфирующей способности: Pb, Cd, Mg, Sn, Al, Mo, Cu, Ti. В сплавах большая способность гасить колебания обычно обусловлена сильной структурной неоднородностью, например в се­ром чугуне из-за наличия графитных включений.

Не меньший интерес вызывает внутреннее трение как метод исследования тонкой структуры металлов и сплавов. Особенно ценную информацию этот метод дает о концентрации и подвиж­ности точечных дефектов, дислокационной структуре, кинетике начальных стадий старения, в том числе деформационного и т. д.

Для экспериментальной оценки величины внутреннего тре­ния необходимо знать связь между напряжением и деформацией при нагружении и разгрузке (см. рис. 6). В принципе эту связь можно найти в результате простых статических испытаний. Но из-за малых абсолютных значений деформации в упругой области сделать это с достаточной точностью довольно сложно. Поэтому на практике обычно используют динамические методы с перио­дическим изменением нагрузки, например по синусоидальному закону. Такому изменению нагрузки будет соответствовать и пе­риодическое изменение деформации, но из-за явления неупру­гости деформация неизбежно будет отставать от напряжения по фазе на какой-то угол φ. Величина tgφ — одна из характеристик рассеяния энергии колебаний, т.е. внутреннего трения. Другую характеристику можно получить, оценив площадь петли, кото­рая пропорциональна величине потерь Δ W энергии колебаний за один цикл. За меру внутреннего трения принимают величину Δ W/2 π W, где W — полная энергия деформации.

Еще одна из характеристик внутреннего трения — логариф­мический декремент затухания амплитуды колебаний γ. Он равен натуральному логарифму отношения предыдущего максимально­го отклонения колеблющегося образца к последующему.

Названные характеристики внутреннего трения связаны меж­ду собой:

tgφ ~ γ / π ~ Δ W/2 π W= Q^-1

где Q^-1 — широко используемое обозначение внутреннего тре­ния.

Равенство обычно хорошо выполняется при Q^-1<0,1 и справедливо для большинства реальных случаев.

Все рассмотренные характеристики внутреннего трения явля­ются разновидностями наиболее важного для металлов релакса­ционного внутреннего трения, которое связано с так называе­мым динамическим гистерезисом. Он возникает в тех случаях когда под действием приложенного напряжения в материале про­исходят какие-то перестройки, требующие времени. Неупругая
деформация при упругом последействии — типичный для метал­лов пример протекающего во времени релаксационного процесса. Для релаксационного внутреннего трения характерны зависимость от частоты колебаний и температуры и независимость от ампли­туды колебаний.

Дата добавления: 2014-01-05