Композиционные материалы

Классификация композиционных материалов (КМ)

Крупнейшим достижением в материаловедении за последние полвека является создание так называемых композиционных материалов. Большой интерес к ним обусловлен высоким уровнем свойств:

- высокой прочностью;

- высокой жесткостью;

- высокой жаропрочностью;

- значительным сопротивлением распространению трещин и др.

В отличие от обычного конструкционного материала композиционный материал (КМ) – искусственный продукт, не встречающийся в природе, его компоненты выбирают и рассчитывают преднамеренно. КМ содержит по крайней мере две различные химические фазы и его свойства определяются свойствами этих фаз.

Основная идея создания КМ – получить комбинацию свойств, которые не присущи каждому материалу в отдельности.

Традиционно применяемые металлические и неметаллические материалы в значительной мере достигли своего предела конструктивной прочности. Вместе с тем развитие современной техники требует создания материалов, надежно работающих в сложной комбинации силовых и температурных полей, при воздействии агрессивных сред, излучений, глубокого вакуума и высоких давлений. Зачастую требования, предъявляемые к материалам, могут носить противоречивый характер. Удовлетворить эти требования можно путем использования композиционных материалов.

Принцип построения КМ человек позаимствовал у природы. Типичными композиционными материалами являются стволы растений, стебли деревьев, кости человека и животных.

Как известно, для оценки эксплуатационных характеристик конструкций существует квадратно-кубическая зависимость: прочность и жесткость повышаются пропорционально квадрату линейных размеров (поперечное сечение), в то время, как масса растет пропорционально кубу (объем) линейных размеров. Т.е. для достижения высоких значений жесткости и прочности должны быть использованы новые высокопрочные и более жесткие материалы, чтобы масса в известном смысле не опережала механические характеристики.

Важной характеристикой в свете этого является удельный модуль упругости Еуд=G/γ. Промышленные материалы, такие, как сталь, алюминий, титан, стекло – имеют близкие значения Е_УД. Для его увеличения конструктор вынужден, в основном, использовать материалы с более низкой плотностью γ и увеличенным размером сечения.

Композиционный материал – это материал, состоящий из двух или нескольких компонентов, отличных по своей природе и химическому составу.

Компоненты образуют единую структуру с границами раздела.

Компонент, непрерывный во всем объеме материала, называется матрицей. Компонент (компоненты) прерывистые, разъединенные матрицей, называются арматурой или армирующим компонентом (фазой). Понятие «армирующий» означает «введенный с целью изменения свойств материала», но всегда «упрочняющий».

КМ принято классифицировать по нескольким основным признакам:

- по материалам матрицы и арматуры;

- по структуре – геометрии и расположению компонентов;

- по методу получения;

- по области применения, впрочем, этот принцип классификации используется редко, т.к. разные материалы могут иметь одно применение (или один и тот же материал использоваться для различных целей).

Классификация по материалам

1. КМ на основе металлов и сплавов. Чаще всего используется Al, Mg, Ti, Cu и сплавы на их основе;

2. КМ на основе интерметаллидов, т.е. химических соединений «металл–металл», например TiAl, Ti₃Al, NiAl, Ni₃Al и др.;

3. керамические КМ – соединения оксидов, карбидов, нитридов, обладающие высокой жаропрочностью;

4. КМ на основе неметаллов, например на основе углерода;

5. КМ с матрицей из полимеров.

Классификация по структурным признакам

1. Волокнистые КМ (ВКМ);

2. Слоистые КМ;

3. Дисперсно-упрочненные КМ (ДУКМ или ДКМ).

Классификация по методам получения

1. Химические методы, связанные с химическим, электрохимическим и термохимическим осаждением или напылением;

2. Твердофазные методы совмещения матрицы и арматуры (методы порошковой металлургии, сварка взрывом, обработка давлением и т.д.);

3. Жидкофазные методы - пропитка волокон расплавом матрицы на воздухе, в вакууме или инертном газе и др.;

4. Комбинированные методы.

Волокнистые композиционные материалы

Несущим элементом волокнистых композиционных материалов (ВКМ) является волокно, проволока. Эти компоненты имеют высокую прочность, высокий модуль упругости и, как правило, невысокую плотность. Именно волокна определяют уровень свойств композиционных материалов. Наиболее перспективными являются волокна бора и углерода. Они используются для упрочнения матриц из Al, Mg, Ti.

Приведем для сравнения свойств армирующих компонентов следующую таблицу.

Свойства волокон, проволоки и нитевидных кристаллов («усов»).

Материал	Тпл,^0С	Плотность γ, г/см3	σВ, МПа	Е, МПа		Удельные характеристики
,	,
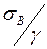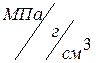
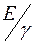Углеродное волокно	~3000 (разла-гается)	1,7	~2500	25·10^5			1,5·10^5
Стальная проволока		7,8	~3800	21·0^5			0,25·10^5
«Усы» карбида кремния		3,21	~37000	5,8·10^5			1,8·10^5

Матрица скрепляет волокна, защищает от механических повреждений и окисления, передает нагрузку на волокна. При разрушении некоторых волокон матрица перераспределяет напряжения. Состояние поверхности раздела компонентов оказывает существенное влияние на поведение КМ. Эта поверхность представляет собой некоторую область, где протекают различные процессы – растворения, образования новых фаз, перераспределения примесей. Некоторые следователи склонны считать поверхность раздела еще одной фазой.

ВКМ находят применение в авиационной и космической технике, судостроении, автомобилестроении, металлургии, химической промышленности, медицине (ортопедии). Их используют для изготовления корпусных элементов, обшивки, силовых конструкций, поршней, лопаток компрессоров, турбин, протезов, медицинских инструментов. В технологическом отношении необходимо отметить, что правильно выбранная технология оказывает существенное влияние на свойства КМ. При этом следует исходить по крайней мере из 3-х условий. Во-первых, техпроцесс должен обеспечить равномерное распределение волокон при заданном их объемном содержании; они должны быть изолированы между собой слоем матрицы. Во-вторых, механическое повреждение волокон должно быть сведено к минимуму. В-третьих, взаимодействие волокон с окружающей средой и с матрицей в процессе их совмещения и снижение при этом прочности волокон должно быть минимальным.

Механическое поведение ВКМ.

Армирование волокнами дает возможность получать наиболее эффективное упрочнение.

Требования к волокнам:

- высокая прочность;

- высокий модуль упругости;

- легкость изготовления и низкая стоимость;

химическая стабильность.

Разрушение ВКМ состоит из ряда последовательных дискретных этапов. В каждом из них происходит перераспределение напряжений. Трещина возникает в матрице и, развиваясь, встречает препятствие на границе раздела «волокно-матрица». Наступает период относительной стабильности. В подобных композитах сочетаются два противоположных свойства – высокий предел прочности за счет использования высокопрочных волокон и достаточная вязкость разрушения за счет пластичного материала матрицы.

Дадим оценку прочности ВКМ с непрерывными волокнами. В ВКМ непрерывные волокна обычно распределены равномерно по всему объему.

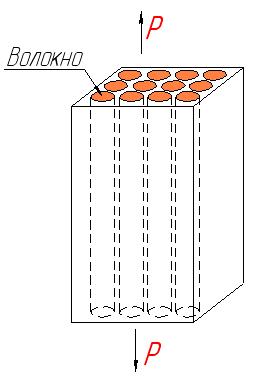
В целях упрощения предположим, что они однородны, прочно скреплены с матрицей так, что при деформировании между ними отсутствует проскальзывание, т.е. деформации композита, волокон и матрицы равны.

.

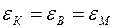Схематично кривая «напряжение-деформация» выглядит следующим образом и имеет 4 характерные стадии.

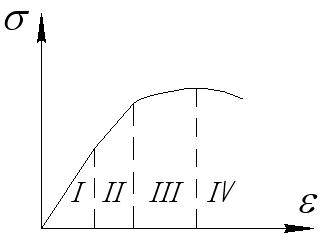
I стадия: упругое волокно и упругая матрица (деформация невелика, оба компонента работают в упругой области).

II стадия: упругое волокно, пластичная матрица (линейна зависимость сохраняется, т.к. модуль упругости волокна много больше модуля упругости матрицы 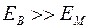, объемная доля волокон высокая и поведение композита определяется свойствами волокон).

III стадия: пластичные волокно и матрица.

IV стадия: разрушение волокна.

Поведение композита с непрерывными волокнами проще представить, если рассматривать следующую модель.

Здесь σ - растягивающие напряжения, действующие на поперечное сечение ;

τ – напряжения сдвига, воздействующие на площадь .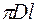

Пусть к образцу из ВКМ приложена осевая нагрузка P, которая связана с напряжением соотношением

,

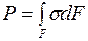где F – площадь поперечного сечения стержня.

Предположим также, что поверхность разрушения плоская; тогда разрушающая нагрузка P_max связана с осевым напряжением разрушения σ_max аналогичным образом:

.

Определим теперь прочность КМ при растяжении

.

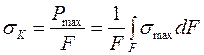Поскольку поверхность разрушения проходит через оба компонента, можно записать

,

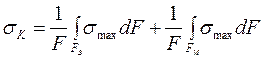где F_В – площадь волокон в поперечном сечении; F_М – площадь матрицы.

Это уравнение можно переписать в ином виде

,

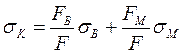где σ_В – средняя прочность волокон в композиции; σ_М – среднее напряжение течения в матрице в момент разрушения.

Если в любом поперечном сечении относительная площадь волокон и матрицы одинакова, то последнее уравнение принимает вид

,

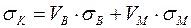где V_B и V_M – объемные доли волокон и матрицы соответственно.

.

Это уравнение называется правилом смеси или аддитивности. Оно широко используется для расчета прочности композиций.

При выводе правила смеси предполагали, что между составляющими композита существует прочная связь. Это означает равенство деформаций разрушения .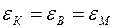

Правило смеси имеет определенные границы применения. Это связано с существованием верхней и нижней границ объемных долей волокон 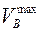и , что в свою очередь определяется технологическими возможностями. При очень плотной укладке волокон матричный материал почти отсутствует, как показано ниже.

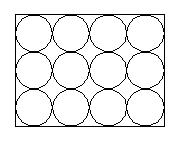
Плотная укладка

И, напротив, доля волокон слишком мала, упрочнение незначительно:

V_В слишком мало

В силу указанных причин для ВКМ существует понятие оптимальной объемной доли волокон.

Примечание: При малых деформациях правило аддитивности для напряжений можно записать как

.

Это уравнение выполняется до тех пор, пока не будет достигнута деформация разрушения одной из структурных составляющих.

Разрушение ВКМ с непрерывными волокнами.

Характер разрушения ВКМ зависит от объемного содержания волокон и матрицы и соотношения их деформаций до разрушения.

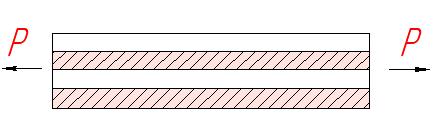
до разрушения.

а) однократное разрушение.

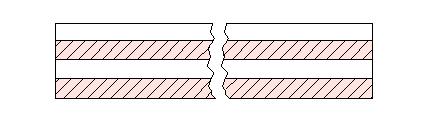
Ему соответствует диаграмма разрушения

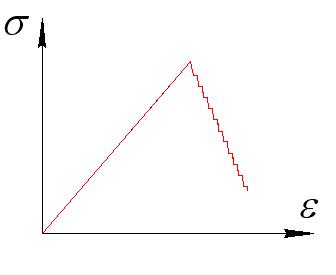
б) множественное разрушение

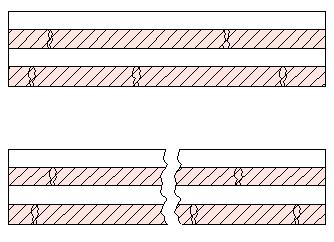
Диаграмма разрушения при этом имеет вид

Волокна дробятся на меньшие длины. Ниспадающие ветви диаграммы соответствуют вытягиванию концов разорвавшихся волокон из матрицы.

Матрица и волокна могут разрушаться не в одной плоскости.

ВКМ, обладая высоким пределом прочности и еще меньшей пластичностью, чем высокопрочные сплавы, имеют, однако, меньшую чувствительность к концентраторам напряжений и большое сопротивление усталостному разрушению. Это объясняется тем, что у материалов различный механизм развития трещин. В традиционных изотропных высокопрочных сталях и сплавах развитие трещин идет прогрессирующим темпом.

В КМ трещина обычно возникает в матрице и, развиваясь, встречает препятствия на границе раздела «матрица-волокно». Волокна тормозят развитие трещин и наступает период относительной стабильности, в течение которого развитие трещин приостанавливается.

Влияние ориентации волокон.

Волокна не всегда параллельны действующей нагрузке. По расположению компонентов (схемы армирования) КМ могут быть разделены на 3 группы:

1. Композиты с одноосным (линейным) расположением армирующего компонента. Волокна, проволоки или нитевидные кристаллы располагаются в матрице в плоскостях, параллельных друг другу.

2. Композиты с двухосным (плоскостным) расположением армирующего компонента, составляющие которого в виде волокон, фольг, матов из нитевидных волокон и т.п. расположены в матрице в плоскостях, параллельных друг другу.

3. КМ с трехосным (объемным) расположением компонентов, когда невозможно выделить одно или два преимущественных направления в материале.

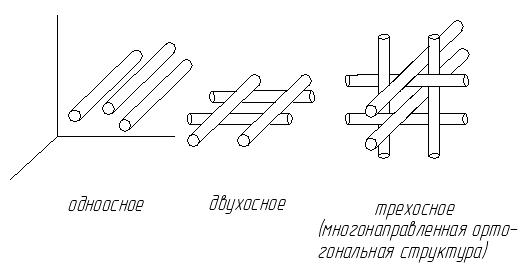
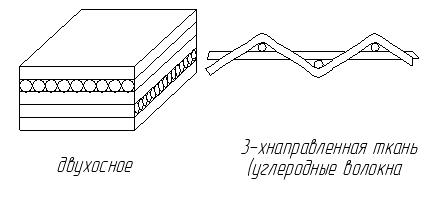
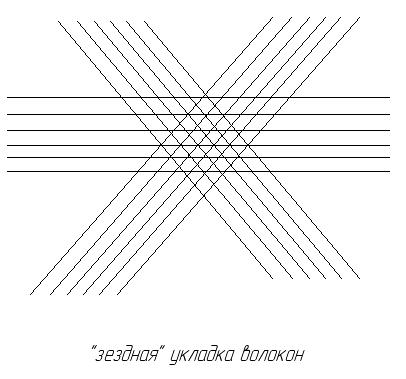
Размер пучка нити, шаг пучков, плотность упаковки нити в каждом направлении характеризуют свойством ткани.

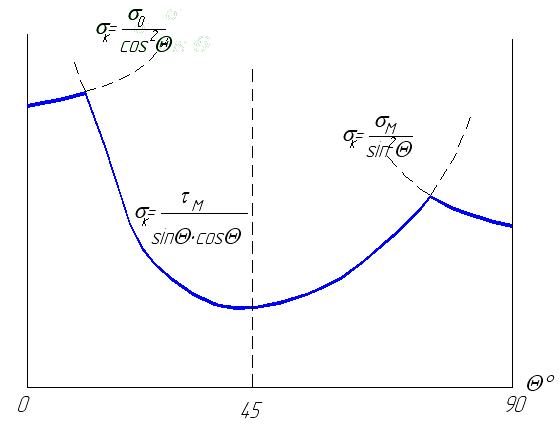
Пусть Θ – угол между направлением (ориентацией) волокон и направлением нагрузки однонаправленного ВКМ.

1. При небольших Θ разрушение происходит вследствие разрыва волокон.

2. При средних значениях Θ – в результате сдвига матрицы по плоскости, параллельной волокнам, либо по поверхности раздела.

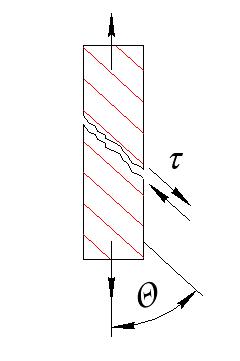
3. При больших углах Θ – либо путем разрыва матрицы, либо по поверхности раздела путем отрыва.

Если принять, что σ₀ – прочность композита при Θ=0⁰;

τ_м – предел прочности матрицы на сдвиг;

σ_м – предел прочности матрицы при растяжении, то графически зависимость прочности композита σ_К от угла Θ выг8лядит следующим образом

Волокнистые композиционные материалы с дискретными волокнами.

Здесь, как и в предыдущем случае, обратим внимание скорее на качественную сторону вопроса без достаточно строгого вывода основных формул.

В том случае, когда армирующие волокна непрерывны, напряжения в них постоянны по всей длине за исключением концевых участков. При малом разбросе частных значений прочности волокон в момент разрушения композиции напряжения почти во всех волокнах достигают их предела прочности. Если же композиция армирована короткими волокнами или усами, то активная роль матрицы состоит в том, чтобы путем пластической деформации передать напряжения волокнам и нагрузить их. В КМ с непрерывными волокнами (особенно высокопрочными) активная роль матрицы состоит скорее в том, чтобы «сплотить» волокна, заставить их работать как единое целое.

Матрица передает нагрузку в результате сдвиговых напряжений на поверхность волокна вблизи разрушенных волокон.

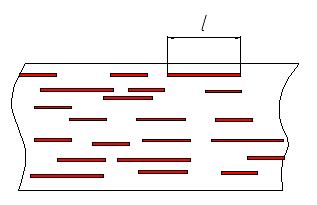
Рассмотрим распределение напряжений в волокне конечной длины l, находящемся в материале матрицы. При этом будем считать, что волокно и матрица работает в упругой области. Если нагрузка приложена к матрице, то в упругой области последняя удлиняется пропорционально напряжению.

Модули упругости соотносятся как - это условие является основным для получения композиции с более высокими механическими свойствами. Т.е. волокно будет ограничивать свободное удлинение матрицы в соседней с волокном зоне.

Рассматриваем отдельно взятое волокно, окруженное матрицей. Влияние других волокон в нашей модели исключается.

Ненагруженное состояние

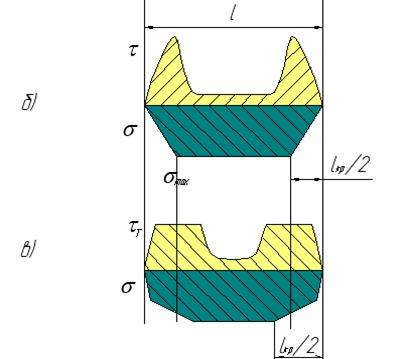
Схема совместной деформации волокна и матрицы (а) и эпюры распределения растягивающих напряжений в волокне и напряжений сдвига на поверхности раздела «волокно – матрица» в упругом (б) и упруго – пластическом приближении (в).

На некотором удалении от волокна матрица свободно и равномерно пластически удлиняется, тогда как в прилегающей к волокну зоне удлинение матрицы будет равняться упругому удлинению последнего. Это приводит к возмущению поля деформации в прилежащей к волокну зоне. По мере удаления от волокна его возмущающее действие ослабевает, пока полностью не сойдет на нет.

Предполагается, что между волокном и матрицей существует идеальная связь и отсутствует передача напряжений через торцы волокна. Это распределение растягивающего напряжения σ вдоль волокна показано на рисунке б.

Поскольку нагрузка не передается через торцы волокна, то растягивающее напряжение увеличивается от нуля на его концах до максимального значения в точке l_кр/2. Критическая длина lкр определяется как длина короткого волокна, которая необходима для достижения напряжения, равного напряжению в волокне бесконечной длины.

Распределение касательных напряжений τ вдоль поверхности раздела нетрудно найти, если рассмотреть равновесие сил, действующих на элемент волокна. Касательные напряжения максимальны на концах волокон и минимальны в середине волокна (рис.б).

Анализ отношения τ_max/σ_max показывает, что максимальные касательные напряжения на поверхности раздела могут достигать 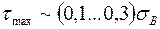и превышать предел текучести матрицы. В этом случае матрица пластически деформируется, и эпюры напряжений будут такими, как это показано на рис. В. При небольшой растягивающей нагрузке изменение касательных напряжений определяется упругим поведением матрицы. По мере увеличения нагрузки максимальные значения ограничиваются пределом текучести матрицы τ_Т.

Таким образом, упругопластическое поведение матрицы представляется более вероятным в процессе работы композиции. За пределами упругой области длина передачи нагрузки и, следовательно, l_кр зависят от напряжения разрушения волокна. Эту зависимость легко получить из уравнения равновесия элементов волокна и матрицы в предположении равенства τ пределу текучести матрицы τ_Т.

,

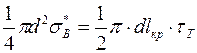откуда ,

где - напряжение разрушения волокна.

Из этого выражения следует, что критическая длина волокна l_кр возрастает пропорционально напряжению разрушения волокна.

В рассмотренной выше модели не учитывалось влияние соседних волокон на распределение напряжений и деформацию. Существуют работы, где приводятся расчеты распределения σ вдоль оси волокна и распределения τ по периметру волокна в зависимости от расположения соседних волокон.

Дата добавления: 2014-01-05