Вероятность безотказной работы

Вероятность безотказной работы (ВБОР) - это вероятность того, что в пределах заданной наработки отказ объекта не наступит.

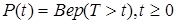
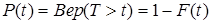(2.4.)

В случае, когда 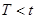или 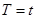имеет место отказ объектов. Следовательно, вероятность отказа:

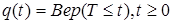
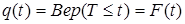(2.5.)

Оба события: 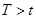- объект работоспособен и 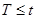- отказ объекта - являются противоположными, следовательно:

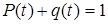(2.6.)

Нахождение обеих вероятностей через функцию F(t) не сложно:

q(t)=Вер.[T £ t]=F(t) (2.7.)

P(t)=Вер.[T > t]=1-F(t) (2.8.)

Учитывая выражения (2.2), (2.7), (2.8), можно записать:

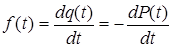(2.9.)

С другой стороны, учитывая выражение (2.3.), получаем формулы вероятности отказа и ВБОР:

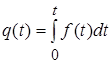, (2.10.)

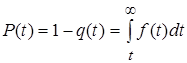(2.11.)

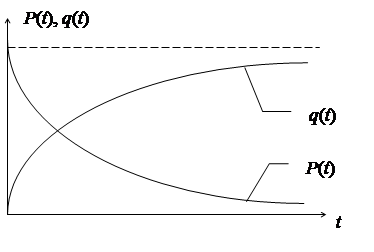Рис.2.1. Графики функций P (t) и q (t).

Рис.2.2. Определение P (t) по графику функции f (t).

График функции ВБОР, приведенный на рис. 2.1., показывает, что p(t) - убывающая функция. Т.о., для определения ВБОР p(t) в интервале нароботки (0, t) необходимо по формуле (2.8.) из единицы вычесть значение фуекции F(t) либо определить площадь под кривой ¦(t) в пределах от t до t = ¥. Вероятность отказа q(t) находим по формуле (2.7.) либо как площадь под кривой ¦(t) в пределах от 0 до t.

Основные свойства показателя безотказности - ВБОР:

1) P (t) есть расчетная величина вероятности работоспособного состояния объекта в интервале наработки (0, t), т.е. априорная величина, определяемая до начала эксплуатации.

2) P (t) есть убывающая функция, а q (t) возрастающая функция.

3) P (t) рассчитывается через вероятностные функции F (t) или f (t)

2.4. Условная ВБОР в интервале наработки (t, t+t), следующим за

интервалом (0, t) безотказной работы.

Обозначим символом А событие, заключающееся в том, что в интервале (0, t) отказ не наступит:

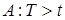
а символом В событие, заключающееся в том, что отказ наступит где-то во всем интервале наработки (0, t+t),

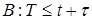
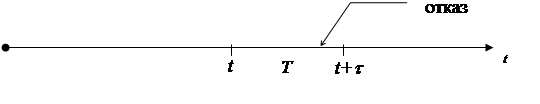Рис. 2.3. Диаграмма наступления первого отказа в интервале (t, t+t)

Событие, заключающееся в том, что отказ не наступит в интервале (0, t), а наступит после момента t и именно в интервале (t, t+t) определяется, как произведение (пересечение) событий А и В, т.е. совместное появление событий А и В:

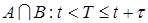
По теореме умножения вероятностей вероятность совместного появления двух событий равна произведению вероятностей одного из них (безусловного) на условную вероятность другого, найденную при условии, что первое событие наступило:

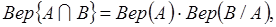(2.12.)

где: Вер(А) – безусловная вероятность события А – отказ до момента t не наступил, т.е. ВБОР в момент t:

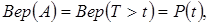(2.13.)

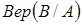- условная вероятность события В при условии, что событие А произошло: вероятность отказа в интервале (t, t+t) при условии, что до момента t отказа не было.

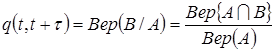(2.14.)

Т.к. Вер(А) найдена согласно (2.13.), нужно определить 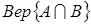и тогда получим выражение q(t, t+t), после чего найдем искомую ВБОР в интервале (t, t+t), следующим за интервалом безотказности (0, t).

В свою очередь:

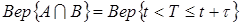или (2.15.)

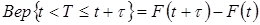(2.16.)

Т.е. это вероятность попадания случайной величины в интервал наработки (t, t+t). Известно, что эта вероятность в свою очередь равна разности функций распределения вероятностей в моменты (t+t) и t.

Учитывая формулы (2.7) и (2.16), можно записать 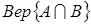в виде:

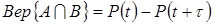(2.17.)

Таким образом, условная вероятность первого отказа в интервале (t, t+t), следующим за интервалом безотказности (0, t) равна

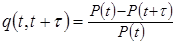(2.18)

Искомая условная ВБОР в интервале (t, t+t), следующем за интервалом безотказности (0, t), P (t, t+t) = 1- q (t, t+t), равна:

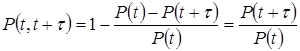(2.19)

Таким образом, ВБОР в интервале (t, t+t), следующим за интервалом безотказности (0; t), есть условная вероятность события, противоположному событию В при ранее разобранном выше условии и определяется как отношение ВБОР в конце искомого интервала (t+t) и ВБОР в начале интервала. Это справедливо для любых функций распределения F(t), т.е. является общим теоретическим изложением. Условно ВБОР в интервале (t; t+t), следующим за интервалом безотказности (0; t), сравним с безусловной ВБОР в интервале (t; t+t). Основной смысл условной ВБОР- какова вероятность того, что объект безотказно проработавший в интервале (0; t), проработает безотказно ещё и в интервале (t; t+t). Эта вероятность определяется выражением (2.19). Безусловная вероятность отказа в интервале (t; t+t) - это вероятность произведения (пересечения) событий А и В и определяется формулами (2.15)-(2.17), следовательно безусловная ВБОР в интервале (t; t+t) определяется как:

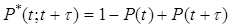(2.20)

Если безусловная вероятность отказа в интервале (t; t+t) есть вероятность того, что наработка до отказа Т попадает в указанный интервал и определяется по формулам (2.16) и (2.17), то условная вероятность отказа в этом интервале учитывает, что объект должен обязательно проработать в интервале (0; t) и определяется формулой (2.16). Ясно, что условная вероятность отказа больше, чем безусловная, т.к. P(t) в знаменателе формулы (2.18) меньше единицы, следовательно условная ВБОР P(t+t) будет меньше, чем безусловная P*(t+t), а это значит, что налагаемое условие - безотказная работа в интервале (0; t) - делает меньшими шансы иметь объект работоспособным в интервале (t;t+t), чем в случае, когда этого условия нет.

Дата добавления: 2014-01-05