План розрахунку

1. Виділити гілки з послідовним з’єднанням елементів і замінити їх еквівалентними;
2. Виділити гілки з паралельним з’єднанням елементів і замінити їх еквівалентними;
3. Пункти 1 та 2 виконувати до того стану, поки не буде отриман контур складаючий одне джерело та один еквівалентний нелінійний елемент;
4. Застосовуючи еквівалентну V/A характеристику нелінійних елементів, а тако ж знаючи 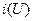, або 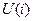визначають 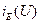, або ;
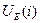5. Виконуючи перетворення у зворотній послідовності та застосовуючи V/A характеристику нелінійних елементів визначаємо 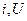всіх нелінійних елементів.

Недолік графічного метода – він має бути застосований тільки для схем простої топології. Його точність досягає не вище за 4...5%.

Аналітичний метод (метод простої ітерації)

Суть метода простої ітерації – послідовне наближення до рішення у наслідок багатократних повторень рішень рівнянь, які складено за законами Кірхгофа для наступного кола.

План розрахунку кола

1. Дана схема заміщення та характеристики нелінійних елементів 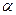та .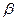

2. Будується таблиця де на нульовому кроку вільно задається 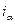та ;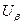

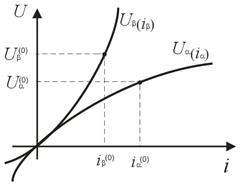
Рис.6. V/A характеристика з’єднання нелінійних елементів кола

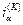
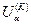
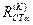
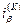
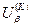
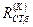
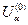
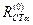
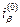
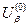
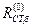
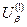
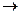
3. Потім по відповідним V/A характеристикам знаходимо відповідні величини – статичні опори:

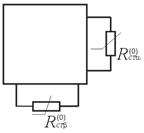
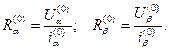(1)

4. У первинній схемі заміщення всі нелінійні елементи замінюються лінійними.

5. Отриману лінійну схему заміщення розраховують будь-яким відомим методом. В наслідок розрахунку необхідно визначити ті величини, якими ми задавалися на нульовому кроку. Це будуть уточнені вирази.

6. Далі процедура повторюється також і доти, поки відмінність попереднього момента від наступного не буде відрізнятися за заданим ступенем точності.

7. По даних таблиці будують графіки.

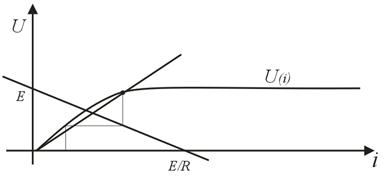
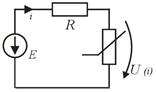
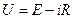
Рис.7. V/A характеристика розрахунку параметрів нелінійних елементів кола

Особливості розрахунку кіл з 1-м нелінійним елементом.

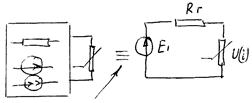
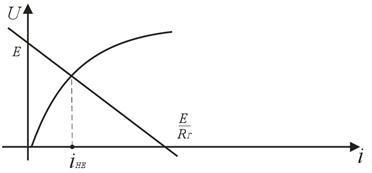
Рис.8. V/A характеристика з’єднання 1-го нелінійного елемента кола

Особливості розрахунку кіл з 2-ма нелінійними елементами.

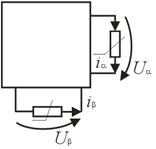
Рис.9. Схеми заміщення кіл з 2-ма нелінійними елементами у виді чотириполюсників

1. Характеристика нелінійих індуктивних елементів

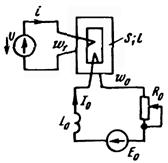
Рис.10

Проста керована нелінійна індуктивна котушка зображена на рис.10. Вона складається з обмотувань 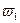і 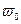, що намотані на замкнуте феромагнітне осердя. Площа поперек перетину осердя , довжина середньої магнітної лінії .

Обмотування 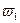, ввімкнено в ланцюг змінного струму, і по ній проходить змінний струм 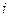, що містить першу і вищі гармоніки. Обмотування керування (підмагнічування) 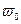приєднана до джерела постійною ЕРС 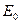через додаткову індуктивність 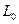і регулюємий резистивний опір 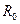. По обмотуванню 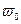протікає постійний струм .

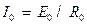Хоча змінний магнітний потік і наводе в обмотуванні 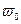змінну ЕРС, але змінний струм по неї практично не проходить, оскільки додаткова індуктивність 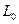утворює для нього (змінного струму) достатньо великий індуктивний опір.

До обмотування прикладена, напруга рівна 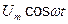. Ця напруга дорівнює ЕРС самоіндукції, узятій із зворотним знаком (активний опір обмотування, вважаємо вельми малим):

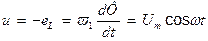. (2)

Звідки магнітний потік

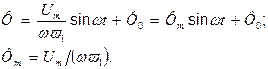(3)

де 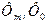— амплітуда змінної і постійної складових магнітного потоку.

Керована нелінійна котушка дозволяє шляхом зміни постійного струму 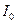в обмотуванні 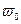керувати змінним струмом .

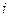Принцип керування режимом її роботи і характер зміни в часі окремих величин показано за допомогою рис.11, а,б, де криві 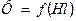є залежними від добутку напруженості магнітного поля 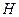на довжину середньої магнітної лінії 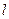осердя.

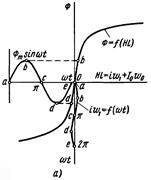
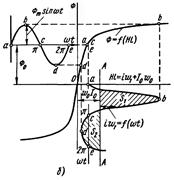
Рис.11, а,б.

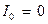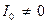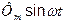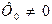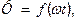
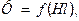
Побудови на рис.11,а відповідають випадку, коли , а на рис.11,б — коли . На обох малюнках змінна складова потоку -одинакова. Для рис.11,а постійна складова потоку, для рис.11,а . На кривих 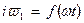найбільш характерні відповідні один одному крапки позначені однаковими буквами.

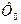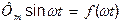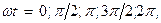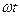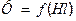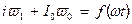Побудови проводимо в такій послідовності. Спочатку відкладаємо значення постійної складової потоку і будуємо криву . Потім довільно задаємося різними моментами часу, наприклад рівними і для кожного значення за допомогою кривої знаходимо відповідні значення і будуємо криву (для рис.11,а 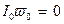). Вісь часу для цієї кривої спрямована вертикально вниз і проходить через крапки а, з, е в нижній частині малюнка.

Струм 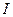не містить постійної складової, оскільки в колі обмотування, немає джерела постійною ЕРС і спрямовувачів.

Пряма А — А (рис.11,б) є нульовою лінією для кривої 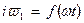. Струм 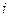змінюється щодо цієї прямої так, що середнє значення його за період від 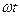=0 до 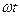= 2л дорівнює нулю. Інакше, проводимо пряму А — А так, щоб площа 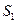, дорівнювала-б площі 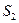. Відстань, на яку видалена пряма А — А від вісі ординат, дорівнює .

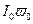Зіставляємо висновки, які стосовні розгляду нелінійного індуктивного елементу, рис.11,а,б.

Зіставними величинами є: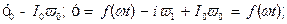

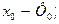
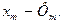
а) Шляхом зміни 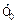можна впливати на амплітуди першої і вищої гармонік функції 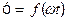, що підтверджується побудовами на рис.11,а,б —амплитуды першою і вищих гармонік функції 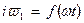залежать від 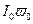(чим більше 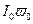, тим більше амплітуда першої гармоніки струму );

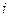б) 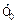залежить не тільки від 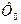, але і від 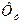; тоді з побудов рис.11,а,б витікає, що і 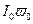залежить не тільки від 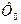, але і від ;

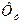в) за наявності постійної складової у складі функції 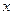в кривій 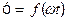з'являються парні гармоніки. З рис.11,б витікає, що за наявностю постійної складової 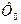у складі магнітного потоку 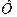в кривій 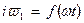з'являються парні гармоніки — крива 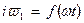несиметрична відносно прямою А — А.

Запишемо потоки через індукції і перетини:

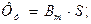(4)

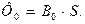(5)

де 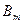— амплітуда змінної індукції, що становить; 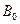— постійна складова індукції. З цих формул витікає, що

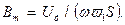(6)

Якщо магнітну індукцію 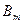виражати в Гс; 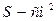; 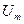замінити на 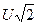, де — діюче значення напруги на обмотуванні 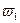, то

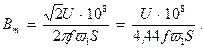(7)

Формула (6) дає можливість знайти амплітуду змінної магнітної індукції за амплітудою синусоїдальної напруги 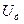, частоті 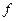, числу витків 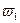і перетину 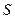. За законом повного струму, добуток напруженості поля 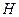на довжину середньої магнітної лінії 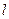повинно бути дорівнювати алгебраічноій сумі МРС:

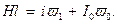(8)

Оскільки струм 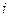містить першу і вищі гармоніки, то рівняння (8) розпадається на ряд рівнянь:

• рівняння для постійних складових;
• рівняння для першої гармоніки;
• рівняння для другої гармоніки і так далі...

Рівняння для постійних складових:

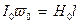(9)

де 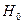— постійна складова напруженості поля.

Змінний струм 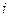містить першу, другу і інші вищі гармоніки, окрім постійної складової, оскільки в ланцюзі обмотки 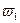, немає джерела постійною ЕРС і спрямовувачів.

Рівняння для першої гармоніки:

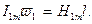(10)

де — амплітуда першої гармоніки струму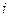, 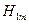— амплітуда першої гармоніки напруженості поля.

Рівняння для другої гармоніки:

(11)

З(9) — (10) витікає, що:

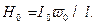(12)

(13)

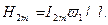(14)

і те інше...

Формула (12) дозволяє визначити постійну складову напруженості поля 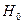через постійну складову струму 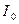. Формула (13) дозволяє знайти 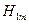через 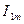і таке інше...

1. Характеристика нелінійих ємностних елементів 500 стр.

Кулон-вольтную характеристику нелінійного конденсатора приблизно можна описати гіперболічним синусом:

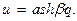(15)

Заряд:

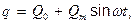(16)

де 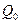—постоянная складова заряду; 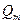— амплітуда першої гармоніки заряду.

При цьому напруга на конденсаторі має постійну складову 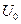, а також першу і вищі гармоніки.

Постійна складова функції 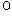конденсатора:

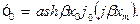(17)

Перша гармоніка функції:

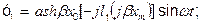(18)

Друга гармоніка функції:

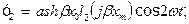(19)

Третя гармоніка функції:

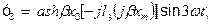(20)

і тому подібне:

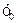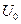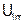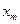Формули (17) — (20) можна розповсюдити на нелінійний конденсатор, якщо замінити на ; на 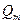; 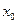на ; на .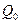

Відповідно до цього постійна складова напруги на конденсаторі

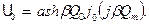(21)

Перша гармоніка напруги

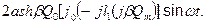(22)

Струм через конденсатор дорівнює . Отже, перша гармоніка струму через нього

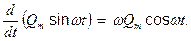(22)

Її амплітуда 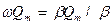, а діюче значення, у 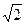~разів менше:

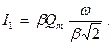(23)

Під ВАХ керуємого нелінійного конденсатора по перших гармоніках розумітимемо залежність значення першої гармоніки струму, що діє, через конденсатор 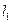від діючого значення першої гармоніки напруги 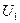, при параметрі .

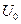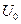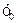На підставі записаної відповідності між і 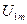і і 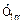і так далі можна стверджувати, що сімейство кривих 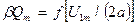, при параметрі 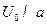повністю повторює сімейство кривих 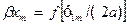, при параметрі , зображено на рис.12,б.

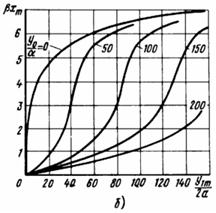
Рис.12,б.

Для переходу від сімейства кривих 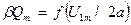до сімейства ВАХ керованого нелінійного конденсатора по перших гармоніках слід врахувати формулу (23) та те, що діюче значення першої гармоніки напруги на конденсаторі:

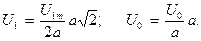(24)

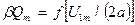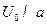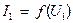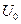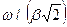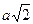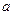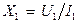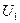Отже, для переходу від сімейства кривих при параметрі до сімейства кривих , при параметрі необходимо масштаб по вісі ординат змінити в раз, по вісі абсцис —раз, параметр — в раз. Подібно до того як для нелінійної індуктивної котушки вводять поняття индуктивного опору по першій гармоніці (див. § 15.25), для нелінійного конденсатора вводять поняття ємнісного опору по першій гармоніці: , де — діюче значення першої гармоніки напруги на конденсаторі; — діюче значення першої гармоніки струму через нелінійний конденсатор; 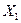— функція 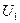та .

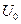1. Нелінійні елементи як генератори вищіх гармонік струму та напруги

Якщо нелінійний елемент, наприклад резистор, приєднати до генератора синусоїдальної напруги, то струм, що проходить крізь нього, матиме несинусоїдальну форму і тому нелінійний резистор буде генератором вищих гармонік струму. Для переконання в цьому, розглянемо рис.13, де крива 1 — ВАХ НР; крива 2— синусоїдальна напруга на нім; крива 3 — струм через НР.

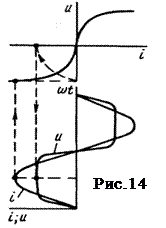
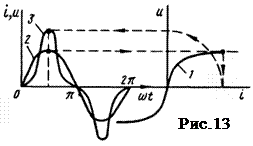
Для побудови кривої 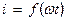послідовно надаємо 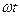значення, рівні, наприклад, 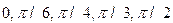і те інше; для кожного з них знаходимо напругу 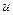і переносимо відповідне значення струму і на криву 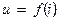і з неї визначаємо значення струму і для узятого моменту часу. Знайдене значення струму і відкладаємо на тій ординаті, якій відповідає вибраний момент часу.

Ці операції показані на рис.13 стрілками. По крапках будуємо криву 3. Вона має пікоподібну форму і може бути розкладена на гармоніки.

Якщо через нелінійний резистор пропустити синусоїдальний струм, то напруга на ньому матиме несинусоїдальну форму. Відповідні побудови приведені на рис.14.

Отже, нелінійний резистор є генератором вищих гармонік напруги. Амплітуди першої і вищих гармонік струмів нелінійно залежать від амплітуд першої і вищих гармонік напруги на нелінійних елементах.

Це утрудняє аналіз і розрахунок нелінійних ланцюгів і в той же час дозволяє здійснити з їх допомогою ряд важливих в практичному відношенні перетворень, принципово нездійсненних за допомогою лінійних електричних ланцюгів при незмінних в часі параметрах.

1. Загальні перетворення, які здіснюють за допомогою нелінійних електричних кіл

Рис.10. Нелінійні чотриполюсники (НЧ) та шести полюсники (НШ)

Нелінійні чотриполюсники (НЧ) та шести полюсники (НШ) в склад яких входять нелінійні елементи. До шестиполюсника додається два затискача керування напругою.

За допомогою чотирьох та шести полюсників можливо здійснювати наступні важливі перетворення:

- змінного струму у постійний (спрямовувачі);

- постійний в змінний (автогенератори);

- множення частоти (подвійники та потрійники);

- поділення частоти (на два, на три...);

- стабілізація струму та напруги;

- ініціювання тригерного ефекту (незначна зміна вхідної напруги визиває скачок зміни вхідної величини);

- модуляція (амплітуда, фаза або частота вхідного сигнала повторює характер зміни керуючого низькочастотного сигнала);

- демодуляція (виділяє з високочастотного - низькочастотний керуючий сигнал);

- перетворення форми вхідної напруги (з синусоідальної форми - трикутну);

- проведення підсилення струму або напруги;

- проведення підсилення потужності;

- проведення ступеневого та логаріфмічного перетворення вхдного сигнала по струму або напрузі...

1. Фізичні явища які спостерігають у нелінійних колах

У колах, які мають нелінійні елементи, спостерігаються фізичні явища, що неможливі в лінійних колах. Найбільш важливі з них:

- виникнення інтенсивних коливань у колі на вищій гармониці при відсутності її у складі вхідного сигналу;

- виникнення субгармонічних коливань (частота якої у n-разів меньше частоти джерела е.р.с.);

- виникнення коливань з частотою 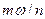де 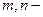цілі числа;

- залежність характера встановленого режима нелінійного кола від попереднього режиму (під час ініціювання тригерних ефектів);

- виникнення автомодуляції (періодична зміна струмів та напруг у колі без впливу зовнішнього модулюючого фактора);

- хаотичне коливання, резонанси.

1. Типи характеристик нелінійних елементів

- характеристики для миттєвих значень (пов’язують миттєві значення основних визначаємих величин. Форма характеристик змінюється при підвищенні швидкості зміни величин за часом);

- ВАХ по першим гармонікам струму та напруги (поділяються на дві підгрупи де: а) напруга (потік, або заряд) на нелінійному елементі змінюється по синусоідальному закону; б) струм на нелінійному елементі змінюється по синусоідальному закону);

- ВАХ для діючих значень показує залежність між діючим значенням напруги на нелінійним елементі і діючим значенням струму що йде по ньому.

1. Питання самоконтролю:

§ Дати поняття нелінійного кола, які умови його дослідження?

§ Привести графічну В/А характеристику нелінійного резистивного елемента та пояснити його властивості, визначення опорів та групп розрахунків?

§ Пояснити визначення параметрів групи еквівалентних нелінійних опорів?

§ Пояснити визначення параметрів джерела напруги і нелінійного елемента?

§ Пояснити визначення V/A характеристики з’єднаних паралельно нелінійних елементів?

§ Пояснити визначення параметрів джерела струму і нелінійного елемента?

§ Написати план розрахунку при паралельно-послідовному з’єднанні нелінійних елементів кола?

§ Пояснити сутність застосування метода простої ітерації для розрахунку пари нелінійних елементів у колі?

§ Написати алгоритм застосування метода простої ітерації для розрахунку пари нелінійних елементів у колі?

§ Пояснити отримання характеристик з’єднання нелінійих індуктивних елементів?

§ Пояснити отримання характеристик з’єднання нелінійих ємностних елементів?

§ Перелічити загальні перетворення, які здіснюють за допомогою нелінійних електричних кіл

§ Які фізичні явища спостерігають у нелінійних колах?

§ Перелічити типи характеристик нелінійних елементів?

Дата добавления: 2014-01-05