Описание структуры кристаллов. Пространственная решетка

Реальная структура кристалла – это конкретное расположение частиц, образующих кристалл, в пространстве. Кристаллу присуще правильное расположение атомов (ионов, молекул) с периодической повторяемостью их в трех измерениях. Такую структуру называют кристаллической решеткой (КР). Модель, описывающая структуру кристалла, может быть представлена некоторой пространственной решеткой, отражающей геометрические параметры структуры. Ввиду периодичности для описания КР достаточно знать расположение частиц в элементарной ячейке, повторением которой путем параллельных дискретных переносов (трансляций) образуется вся структура кристалла. Элементарная ячейка может иметь форму прямоугольного или косоугольного параллелепипеда, квадратной или косоугольной призмы. Размеры ребер элеменарной ячейки a, b, c называют периодами решетки. В кристаллографии существует 14 различающихся по симметрии пространственных трансляционных решеток, называемых решетками Браве.

Существованием кристаллической решетки объясняется анизотропия свойств кристалла, плоская форма их граней, постоянство углов и прочие законы геометрической кристаллографии. В элементарной ячейке кристаллической решетки может быть от одного (для химических элементов) до десятков и тысяч (для соединений) или тысяч и миллионов (белки, вирусы) атомов. Период идентичности составляет от нескольких Å до сотен и тысяч Å. Но везде любому атому данной ячейки соответствует трансляционно идентичный ему атом любой другой ячейки кристалла.

Реальная структура кристалла всегда отличается от идеальной модели. Причин этому много. Атомы могут отличаться по атомному номеру (изоморфизм), по массе ядра (изотопический изоморфизм), в кристалле встречаются дефекты: вакансии, дислокации, примесные атомы и др.

Реальная кристаллическая решетка не является статическим образованием. Атомы и молекулы, образующие КР, колеблются около положений равновесия, причем характер колебаний зависит от симметрии, энергии связи, температуры и других факторов. Известны даже случаи вращения молекулы в КР. С повышением температуры колебания частиц усиливаются вплоть до разрушения КР и перехода вещества в жидкое состояние.

Рассмотрим более подробно модельное описание КР.

На рис.1 представлен для примера фрагмент пространственной решетки, а на рис.2 - элементарный параллелепипед, из которых она построена. В каждом из направлений x, y, z можно выделить бесконечные ряды точек, лежащих на прямых и называемых узлами, которые могут быть получены трансляцией в соответствующем направлении отрезков a, b, c, являющихся периодами (параметрами) решетки. Узлы не обязательно должны совпадать по положению с материальными частицами вещества, это могут быть и точки между частицами. В пространстве решетки можно выделить плоские сетки, которые также получаются трансляцией элементарных параллелограммов, называемых ячейками плоской сетки и вершины которых являются узлами.

Элементарную ячейку можно выбрать по-разному, но принято выбирать ее так, чтобы она удовлетворяла следующим требованиям:

1) наилучшим образом отражала симметрию структуры;

2) по возможности имела бы прямые углы;

3) обладала бы наименьшей площадью.

Если элементарная ячейка не содержит внутри себя узлов, ее называют примитивной. Каждый узел, принадлежащий вершине такой ячейки, принадлежит одновременно четырем ячейкам, а это значит, что на данную ячейку приходится ¼ от этого узла, а в целом на примитивную ячейку приходится один узел. Таким образом, плоскую сетку можно определить как систему одинаковых элементарных ячеек, полученных параллельным переносом, прилегающих друг к другу без промежутков.

Наконец, на основе плоской ячейки можно построить объемную элементарную ячейку, например в виде параллелепипеда (рис.2), трансляцией которой получается объемная решетка, т.е. трехмерная система эквивалентных узлов.

Таким образом, пространственная решетка строится путем трансляции ребер a, b и c, образующей так называемую ячейку трансляций или трансляционную группу. Ее выбор в некоторой степени произволен, но за ребра элементарной ячейки принимают те направления в КР, в которых величина шага трансляции получается наименьшей и наилучшим образом отражает симметрию кристалла.

В общем случае a¹b¹c; a¹b¹g¹90^°. В некоторых случаях удобно характеризовать плоскую или пространственную решетку не примитивной, а сложной элементарной ячейкой, у которой узлы есть не только в вершинах, но и внутри ячеек.

Совокупность координат частиц, входящих в элементарную ячейку, называется базисом ячейки. При этом начало координат выбирается в вершине ячейки и координаты частиц выражаются в долях элементов a, b, c.

Для описания пространственной решетки, отражающей структуру кристалла, применяется метод так называемого кристаллографического индицирования, удобный тем, что он пригоден для любой системы координат. Ниже приведены основные понятия, его характеризующие.

Символы узлов. Если один из узлов решетки выбрать за начало координат, то любой другой узел может быть определен радиусом-вектором R=ma+nb+pc, где m, n, p называются индексами данного узла. Совокупность чисел m, n, p, заключенная в двойных квадратных скобках [[m, n, p]], называется символом узла. Если индекс отрицателен, знак минус ставится над цифрой. На рис.3 приведены для примера символы узлов плоской сетки, а на рис.4 - символы некоторых характерных узлов кубической ячейки.

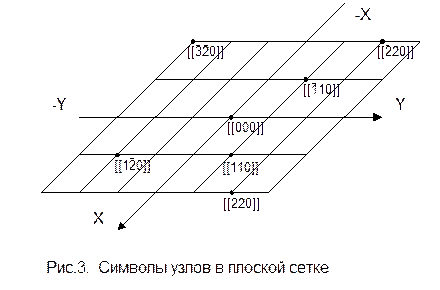
Символы рядов (ребер). Любой ряд узлов в решетке может быть определен двумя точками и задавать направление ряда. Для определения направления множества параллельных рядов достаточно задать направление ряда, проходящего через выбранное произвольно начало координат. Тогда направление задается началом координат (нулевые координаты узла) и любым узлом, координаты которого принимают за символ ряда и пишут в квадратных скобках [m, n, p]. Такой символ характеризует свойство параллельных рядов и параллельных ребер кристаллографического многогранника.

Грани реального кристалла, пересекающиеся по параллельным ребрам, образуют пояс или зону, а общее направление этих ребер называется осью зоны. Символ [m, n, p]

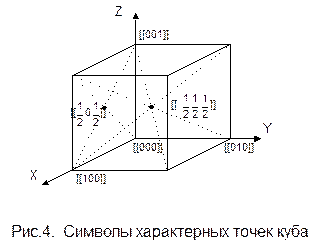характеризует и ось зоны.

На рис.5 показаны символы некоторых направлений в плоской сетке.

Обычно для определения символа ряда выбирают узел, ближайший к началу координат, поэтому если индексы в символе ряда получаются кратные, их можно сократить на целое положительное число.

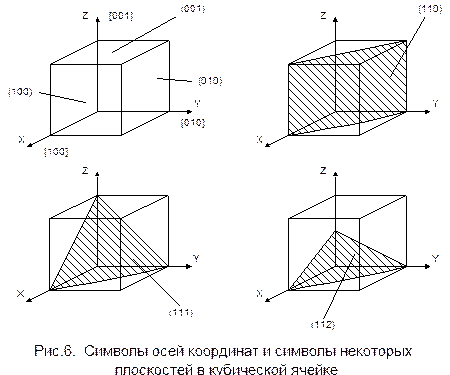
На рис.6 приведены символы осей координат: OX - [100], OY - [010], OZ - [001]. Символы осей координат не зависят от параметров решетки, т.е. от углов между осями координат и осевых отрезков.

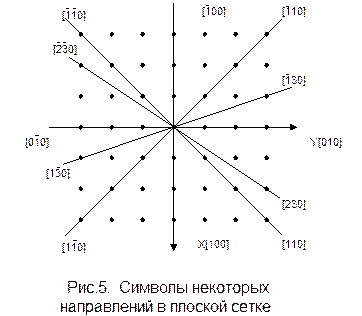Символы плоскостей. Плоскости в пространственной решетке достаточно определить их наклоном в некоторой системе координат. Наклон характеризуется длиной отрезков ma, nb, pc между началом координат и точками пересечения координатных осей с плоскостью. Таким образом, отношение числа m:n:p характеризует наклон всего семейства взаимно параллельных плоскостей. Если отношение m:n:p может привести к взаимнопростым целым числам (включая ¥), то

такое отношение называют отношением параметров Вейсса. Однако в кристаллографии принято использовать не параметры Вейсса, а так называемые индексы Миллера. По существу, это величины, обратные параметрам Вейсса, также приведенные к целым числам. Если параметры Вейсса заданы числами p, q, r, то индексы Миллера определяются из соотношения 1/p:1/q:1/r=h:k:l. Например, если p=3, q=2, r=¥, то p:q:r=3:2: ¥, соотношение обратных величин будет 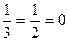, или, после приведения к простым целым числам, индексы Миллера составят h:q:l=2:3:0. Другими словами, индексы Миллера представляют собой величины, обратно пропорциональные длине отрезков, отсекаемых плоскостью на осях координат. Этот символ, помещенный в круглые скобки (h, k, l), называют символом плоскости. Он характеризует наклон всего семейства параллельных плоскостей и означает, что эта система рассекает отрезок а на h частей, b на к частей и с на l частей.

На рис.6 представлены символы некоторых плоскостей в кубической ячейке, включая грани куба. В силу симметрии кристалла вдоль некоторых направлений и плоскостей его физические параметры одинаковы. Поэтому иногда используют обобщенные символы для обозначения таких эквивалентных по свойствам плоскостей и направлений. Так, например, все ребра куба являются эквивалентными. Поэтому для семейства эквивалентных направлений [100], [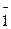00], [010], [0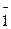0], [001], [00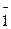] можно ввести один общий символ <100>, или, в общем виде <rst>.

Аналогично для плоскостей (hql), образующих эквивалентное семейство, вводят обобщенный символ íhqlý.

Итак, для описания структуры кристаллов используют следующие системы символов:

[[rst]] – узел в решетке, вершина многогранника;

[mnp] – направление в решетке, ребро кристалла;

(hql) – плоскость в решетке, грань кристалла;

<rst> – комплекс симметрично эквивалентных направлений, совокупность ребер простой формы кристалла;

íhqlý – комплекс симметрично эквивалентных плоскостей, совокупность граней простой формы кристалла.

Дата добавления: 2014-01-05