Элементарные звенья обыкновенных линейных систем

Обыкновенными называют линейные системы с постоянными параметрами. После многократного применения операции расчленения такую систему в конечном итоге можно разбить на не подающиеся дальнейшему расчлененению звенья четырех типов:

- умножающие;

- суммирующие;

- интегрирующие;

- дифференцирующие.

Из названных типов звеньев к динамическим относятся интегрирующие и дифференцирующие. Рассмотрим основные характеристики этих звеньев.

Идеальное интегрирующее звено

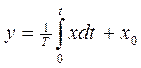
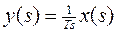
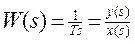
Здесь приняты следующие обозначения: х – входная величина, y – выходная, W(s) – передаточная функция.

Переходная и импульсная переходная функции звена при x(t) = 1(t), x(0) = 0 соответственно равны:

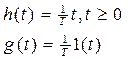
При 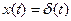выходная функция скачком принимает постоянное значение, которое и сохраняет в дальнейшем. Примером приближенной реализации интегрирующего звена может служить двигатель постоянного тока, у которого постоянная времени мала в сравнении с временем переходного процесса в системе, в которой двигатель работает.

Идеальное дифференцирующее звено

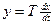
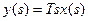
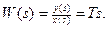
Переходная функция звена при х(t)=1(t) равна 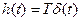. Она представляет собой импульс типа дельта – функции с площадью T.

Возможность представления реального звена идеальным дифференцирующим определяется соотношением постояной времени звена и дифференцируемого процесса. Чем больше инерция звена, тем с большей погрешностью оно будет дифференцировать быстро изменяющиеся функции. О близости реального звена к идеальному удобно судить по частотным характеристикам. Примером звена, близкого к идеальному, может служить тахогенератор, дифференцирующий угол поворота вала машины. Выходное напряжение тахогенератора

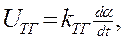
где 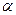- угол поворота вала. Весьма близким к идеальному дифференцирующему звену является дифференцирующий усилитель с большим коэффициентом усиления. В той полосе частот, которая указана в паспорте усилителя, его передаточная функция

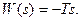
Выходная величина дифференцирующего звена при гармоническом воздействии пропорциональна частоте воздействия, и звено усиливает высокочастотные помехи, что сильно затрудняет его использование. Поэтому в моделирующих устройствах обычно стремятся обойтись без дифференцирующих звеньев. Это всегда возможно, если степень числителя передаточной функции моделирующего звена не выше степени знаменателя. Такую систему можно разбить на звенья только трех типов: масштабные, суммирующие и интегрирующие.

Дата добавления: 2014-01-05