Типовые апериодические звенья первого и второго порядка

При декомпозиции схемы на элементарные звенья она обычно становится чрезмерно детальной, громоздкой и малонаглядной, поэтому в системах автоматического управления широкое применение находит декомпозиция на типовые звенья несколько более сложной структуры, чем элементарные, но более соответствующие реальным элементам.

Неидеальное интегрирующее звено

Строго говоря, любое реальное интегрирующее звено неидеально.

Иногда грубое интегрирование выполняют и с помощью статического звена, напрмер с помощью схемы

для которой можно записать законы Кирхгофа для токов и напряжений соответственно: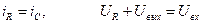

Далее, учитывая определение

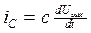
перепишем закон Кирхгофа дл напряжений, получим уравнение вида:

,

откуда следует

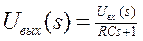
Положив T = Rс, запишем последнее уравнение в виде

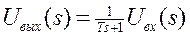
Неидеальное дифференцирующее звено

Рассмотрим схему

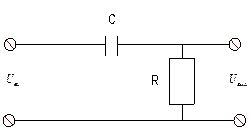
Для этой схемы законы Кирхгофа для токов и напряжений имеют вид:

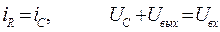
Учитывая, что

,

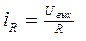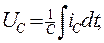
перепишем уравнение Кирхгофв для напряжений

.

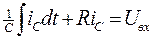Далее применим преобразование Лапласа и перейдем к изображениям и алгебраической переменной s. Будем иметь

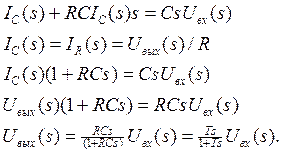
Погрешность замены идеального звена не идеальным можно уменьшить, выбрав T достаточно малым, и вводя большой коэффициент усиления k:

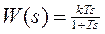
Идеальное форсирующее звено

Введение производных в закон регулирования осуществляется обычно с помощью так называемых форсирующих звеньев. Идеальное форсирующее звено осуществляет сложение выходной величины с ее производной и имеет передаточную функцию

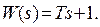
Устойчивое звено первого порядка общего типа

Рассмотрим звено с передаточной функцией

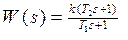
В таком звене при 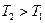преобладает форсирование (дифференцирование), при 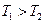- инерционное запаздывание (интегрирование). Поэтому такое звено часто называют интегрирующим. При 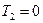оно превращается в часто используемое звено, называемое статическим звеном первого порядка, инерционным, апериодическим.

Колебательное звено

Такое звено имеет дифференциальное уравнение вида

.

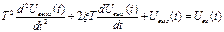Перейдем к изображению Лапласа, получим:

.

.

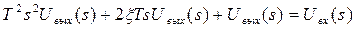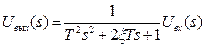Аналогичным образом получены передаточные функции остальных типовых звеньев, результаты внесены в таблицу 2:

Таблица 2.

Тип звена	Передаточная функция
1. Безынерционное звено	k, k = const
2. Идеальное дифференцирующее звено	k s
3. Дифференцирующее звено с замедлением	ks / (1+Ts)
4. Идеальное интегрирующее звено	k / s
5. Интегрирующее звено с замедлением	k / (s (1 + Ts))
6. Апериодическое звено 1-го порядка	k / (Ts+1)
7. Апериодическое звено 2-го порядка	k / (T2s^2+T1s+1)
8. Колебательное звено	k / (Ts^2+2xTs+1)
9. Изодромное звено	k (Ts +1) / s
10. Консервативное звено	k / (T^2 s^2+ 1)

Дата добавления: 2014-01-05