КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление передаточных функций
|
|
|
|
Рассмотрим формулу Мезона определения передаточной функции между двумя произвольными вершинами А и В графа.
,
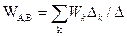где k - количество прямых путей между A и B; Wk - передаточная функция к -го прямого пути, равная произведению передаточных функций, входящих в этот путь ребер;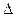 
- определитель графа; 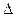k- определитель к - го минора графа, полученного путем удаления всех ребер и вершин, лежащих на к - ом пути, а также всех ребер, входящих и исходящих из этих вершин. Такой определитель вычисляется по формуле:
где Wi - передаточные функции различных контуров; Wi Wj - произведение передаточных функций несоприкасающихся пар контуров; Wi Wj Wl - произведение передаточных функций несоприкасающихся троек контуров и т.д. Под прямым путем между двумя заданными вершинами графа будем понимать непрерывную последовательность ветвей одного направления, при прохождении которой каждая вершина встречается не более одного раза. Под контуром будем понимать непрерывную последовательность ветвей одного направления, при прохождении которой можно вернуться к вершине начала прохождения, причем каждая вершина внутри контура встречается не более одного раза.
|
|
|
Дата добавления: 2014-01-05; Просмотров: 504; Нарушение авторских прав?; Мы поможем в написании вашей работы!