Характеристическое уравнение. Понятие корневого годографа

Передаточную функцию разомкнутой системы управления можно представить в виде:

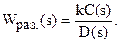
Здесь k - числовой коэффициент, в который в качестве сомножителя входит коэффициент усиления сигнала в прямой цепи. Передаточная функция замкнутой системы управления с единичной отрицательной обратной связью определяется по формуле:

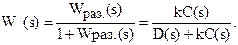
Уравнение D(s) + kC (s) = 0 называется характеристическим. Его корни называются полюсами, а корни уравнения k C(s) = 0 называются нулями. Полюса и нули могут рассматриваться в качестве динамических характеристик наряду с переходными и частотными. При изменении k от 0 до бесконечности полюсы описывают в комплексной плоскости траектории, называемые корневым годографом.

По движению полюсов вдоль траекторий судят о свойствах системы управления. Отметим несколько основных свойств корневого годографа:

- корневой годограф симметричен относительно действительной оси

- действительная ось принадлежит корневому годографу

- число ветвей корневого годографа определяется степенью характеристического уравнения.

Основное аналитическое уравнение траектории корней имеет вид алгебраического уравнения:

-

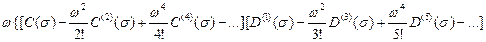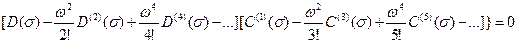
Это уравнение позволяет по задаваемому значению 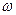найти 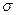, то есть построить точки корневого годографа. Здесь приняты следующие обозначения: C(s), D(s) - полиномы C(s) и D(s) соответственно после подстановки s = s. 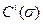, 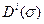- производные этих полиномов. Для многомерной системы управления число характеристических уравнений будет определяться числом управляемых параметров. Если все каналы управления связаны между собой, то характеристические уравнения всех каналов будут одинаковые.

Дата добавления: 2014-01-05