Побудова купи

Купа

Видалення елементу

Параметром для процедури є вказівник на вершину, що видаляється. Тут можливі три варіанти дій:

якщо у вершини немає дітей, достатньо помістити NULL у відповідне поле його батька (замість вказівника на вершину, що видаляється)

якщо у вершини є одна дитина, можна з'єднати батька цієї вершини безпосередньо з її дитиною

якщо вершина має двох дітей, слід спочатку знайти слідуючий (в сенсі порядку) елемент y, в якого немає лівої дитини, а потім скопіювати значення та додаткові дані з вершини y на місце вершини, що видаляється, а саму вершину y видалити.

DELETE (T, z)

1 if left[z] = NULL or right[z]=NULL

2 then y:=z

3 else y:=SUCCESSOR(z)

4 if left[y] <> NULL

5 then x:=left[y]

6 else x:= right[y]

7 if x <> NULL

8 then p[x]:=p[y]

9 if p[y]:=NULL

10 then root[T]:=x

11 else if y=left[p[y]]

12 then left[p[y]]:=x

13 else right[p[y]]:=x

14 if y <> z

15 then val[z]:=val[y]

16 //копіювання додаткових даних з y

17 return y

КУПА або піраміда (англ. heap) в інформатиці -- спеціалізована деревовидна структура даних, в якій існують певні властивості впорядкованості. Така структура даних повинна задовільняти основній властивості купи:

нехай А та B -- елементи купи, такі що B підпорядковане A (B - дитина А). Тоді значення B не повинно перевищувати А, тобто val[B] ≤ val[A]

Найбільш уживаним класом куп є бінарні купи.

Базові операції з купою такі:

підтримка основної властивості купи

побудова купи з невпорядкованого масиву

сортування купи

видалення найменшого елемента

отримання найбільшого елемента

додавання елемента

Купи часто використовуються для моделювання черг з пріоритетами.

А) Бінарна купа

Бінарна купа (англ. binary heap) — це структура даних, що є масивом, який можна розглядати як майже повне бінарне дерево. Кожен вузол цього дерева відповідає певному елементу масиву. На всіх рівнях, крім, можливо останнього, дерево повністю заповнене (заповнений рівень — такий, що містить максимально можливу кількість вузлів). Останній рівень заповнюється послідовно зліва направо до тих пір, доки в масиві не закінчатся елементи.

Для масиву A у корені дерева знаходиться елемент A[1]. Далі дерево будується за наступним принципом: якщо якомусь вузлу відповідає індекс i, то індекс його батьківського вузла обчислюється за допомогою процедури Parent(i), індекс лівого дочірнього вузла — за допомогою процедури Left(i), а індекс правого дочірнього вузла — за допомогою процедури Right(i):

Parent(i)

return

Left(i)

return 2i

Right(i)

return 2i + 1

Розглядають два види бінарних куп: неспадні і незростаючі. В обох видах значення, що розташовані у вузлах купи, задовільняють властивості купи (англ. heap property). Властивісь незростаючої купи (англ. max-heap property) полягає в тому, що для кожного вузла крім кореневого виконується нерівність:

.

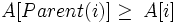Іншими словами, значення вузла не перевищує значення батьківського вузла. Таким чином найбільший елемент знаходиться в корені дерева. Принцип побудови неспадної купи(англ. min-heap) протилежний. Властивість неспадної купи (англ. min-heap property) полягає в тому, що кожен елемент крім кореневого є неменшим за свій батьківський елемент:

.

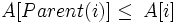Підтримка властивостей купи

Підтримку властивості купи можна здійснювати за допомогою процедури Max_Heapify (для незростаючих бінарних куп). На вхід подається масив A й індекс i цього масиву. При виклику процедури Max_Heapify припускається, що бінарні дерева, коренями яких є елементи Left(i) і Right(i) є незростаючими купами, але сам елемент A[i] може бути меншим за його дочірні елементи і тим самим порушувати властивість незростаючої купи. Процедура Max_Heapify спускає значення елемента A[i] вниз по купі до тих пір, доки дерево в якому цей елемент буде корнем не стане незростаючою бінарною купою:

Max_Heapify(A,i)

1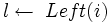

2

3 if 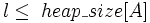і A[l] > A[i]

4 then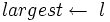

5 else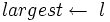

6 if 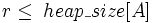і A[r] > A[largest]

7 then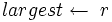

8 if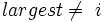

9 then Поміняти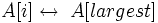

10 Max_Heapify(A,largest)

Час роботи процедури в найгіршому випадку пропорційний висоті купи. Якщо купа складається з n елементів, то її висота log2(n). Тому оцінка часу роботи одного визову Max_Heapify є O(log n).

Для падтримки властивості неспадної бінарної купи можна скористатись процедурою Min_Heapify. Вона повністю подібна до Max_Heapify, тільки в рядках 3 і 6 алгоритму знак ">" треба замінити на "<".

За допомогою процедури Max_Heapify можно перетворити масив A[1 n], де n = length[A], у незростаючу купу. Всі елементи підмасиву 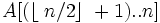є листами дерева, тому кожен з них можна вважати одноелементною купою, з якої можна почати процес побудови. Процедура Build_Max_Heap проходить по всім іншим вузлам і для кожного з них иконує процедуру Max_Heapify:

Build_Max_Heap(A)

1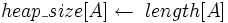

2 for 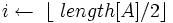downto 1

3 do Max_Heapify(A,i)

По завершенню роботи процедури, масив A організується в незростаючу купу. Час роботи процедури Build_Max_Heap можна записати так:

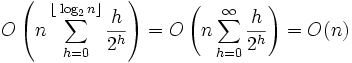
Для створення неспадної купи, необхідно замінити у третьому рядку алгоритма виклик Max_Heapify на Min_Heapify.

Дата добавления: 2014-01-05