Додавання елементу

Дерево

Граф

Граф — пара множин V і E, елементи множини V називають вершинами (англ. vertex), множина E містить впорядковані та невпорядковані пари вершин. Невпорядкована пара вершин називається ребром, впорядкована — дугою.

Граф, який містить тільки ребра називається неорієнтованим, який містить тільки дуги — орієнтованим. Якщо пара вершин сполучається кількома ребрами чи дугами одного напрямку, то ребра (дуги) називають кратними. Дуга чи ребро що сполучає вершину саму із собою називається петлею. Вершини сполучені ребром чи дугою називають суміжними, також називають суміжними ребра, що мають спільну вершину.

Кожен граф можна відобразити в евклідовому просторі множиною точок, які відповідають вершинам, сполучених лініями, що відповідають ребрам (дугам).

Крім того, варто зазаначити, що в сучасній теорії графів існує проблема відсутності уніфікованої термінології. Тому при поданні певного визначення чи поняття із цього розділу дискретної математики треба мати це на увазі. Тут використовується найбільшвживана термінологія — американська

Ось альтернативне і доповнене означення графа.

Простим графом називають пару G=(V,E), де V - скінченна і непорожня множина, елементи якої називають вершинами. E - множина ребер, кожне з яких - це невпорядкована пара різних вершин з V.

Іноді є потреба якусь пару вершин з'яднати більше, ніж одним ребром. Тому вводять означення Мультиграфа. Мультиграфом називають пару G=(V,E), де V - скінченна і непорожня множина, елементи якої називають вершинами. E — сім'я ребер, кожне з яких — це невпорядкована пара різних вершин із V.

Ребра, які з'єднують одну й ту саму пару вершин, називають кратними (перелельними) ребрами.

Подальше узагальнення означення графу полягає у введенні поняття псевдограф. Псевдограф — це пара G=(V,E), де V - скінченна і непорожня множина, елементи якої називають вершинами. E - множина ребер, кожне з яких - це невпорядкована пара (не обов'язково різних!) вершин із V.

Ребро, яке сполучає одну й ту саму вершину, називають петлею.

Розглянуть три типи називають неорієнтованими графами. Псевдограф є узагальненням мультиграфа, а мультиграф у свою чергу - простого графа.

Тип графа	Ребра	Кратні ребра дозволені?	Петлі дозволені?
Простий граф	Неорієнтовані	Ні	Ні
Мультиграф	Неорієнтовані	Так	Ні
Псевдограф	Неорієнтовані	Так	Так
Орієнтований граф	Орієнтовані	Ні	Так
Орієнтований мультиграф	Орієнтовані	Так	Так

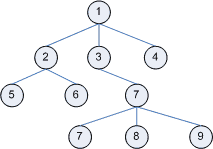
Дерево - в інформатиці та програмуванні одна з найпоширеніших структур даних. Формально дерево визначається як скінченна множина Т з однієї або більше вершин (вузлів, nodes), яке задовольняє наступним вимогам:

існує один виокремлений вузол - корень (root) дерева

інші вузли (за виключенням кореня) розподілені серед m ≥ 0 непересічних множин T1.Tm і кожна з цих множин в свою чергу є деревом. Дерева T1.Tm мають назву піддерев (subtrees) даного кореня.

З цього визначення випливає, що кожна вершина є в свою чергу коренем деякого піддерева. Кількість піддерев вершини має назву ступеня (degree) цієї вершини. Вершина ступеню нуль має назву кінцевої (terminal) або листа (leaf). Некінцева вершина також має назву вершини розгалуження (branch node). Нехай x - довільна вершина дерева з коренем r. Тоді існує єдиний шлях з r до x. Усі вершини на цьому шляху називаються предками (ancestors) x; якщо деяка вершина y є предком x, то x називається нащадком (descendant) y. Нащадки та предки вершини x, що не співпадають з нею самою, називаються власними нащадками та предками. Кожну вершину x, в свою чергу, можна розглядати як корень деякого піддерево, елементами якого є вершини-нащадки x. Якщо вершини x є предком y та не існує вершин поміж ними (тобто x та y з'єднані одним ребром), а також існують предки для x (тобто x не є коренем), то вершина x називається батьком (parent) до y, а y - дитиною (child) x. Коренева вершина єдина не має батьків. Вершини, що мають спільного батька, називаються братами (siblings). Вершини, що мають дітей, називаються внутрішніми (internal). Глибиною вершини x називається довжина шляху від кореня до цієї вершини. Максимальна глибина вершин дерева називається висотою.

Якщо існує відносний порядок на піддеревах T1.Tm, то таке дерево називається впорядкованим (ordered tree) або пласким (plane tree).

Лісом (forest) називають множину дерев, які не перетинаються.

Найчастіше дерева в інформатиці зображують з коренем, який знаходиться зверху (говорять, що дерево в інформатиці "росте вниз").

Важливим окремим випадком кореневих дерев є бінарні дерева, які широко застосовуються в програмуванні і визначаються як множина вершин, яка має виокремлений корінь та два піддерева (праве та ліве), що не перетинаються, або є пустою множиною вершин (на відміну від звичайного дерева, яке не може бути пустим).

Важливими операціями на деревах є:

обхід вершин в різному порядку

перенумерація вершин

пошук елемента

додавання елемента у визначене місце в дереві

видалення елемента

видалення цілого фрагмента дерева

додавання цілого фрагмента дерева

трансформації (повороти) фрагментів дерева

знаходження кореня для будь-якої вершини

Найбільшого розповсюдження ці структури даних набули в тих задачах, де необхідне маніпулювання з ієрархічними даними, ефективний пошук в даних, їхнє структуроване зберігання та модифікація.

А) Бінарне дерево:

В програмуванні бінарне дерево -- дерево структура даних, в якому кожна вершина має не більше двох дітей. Зазвичай такі діти називаються правим та лівим. На базі бінарних дерев будуються такі структури, як бінарні дерева пошуку та бінарні купи.

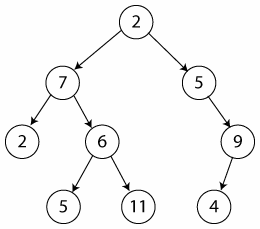Бінарне дерево

Різновиди бінарних дерев

Бінарне дерево -- таке кореневе дерево, в якому кожна вершина має не більше двох дітей.

Повне (закінчене) бінарне дерево -- таке бінарне дерево, в якому кожна вершина має нуль або двох дітей.

Ідеальне бінарне дерево -- це таке повне бінарне дерево, в якому листя (вершини без дітей) лежать на однаковій глибині (відстані від кореня).

Бінарне дерево на кожному n-му рівні має від 1 до 2n вершин.

Обхід бінарного дерева

Докладніше дивись статтю Обхід дерева.

Часто виникає необхідність обійти усі вершини дерева для аналізу інформації, що в них знаходиться. Існують декілька порядків такого обходу, кожний з яких має певні властивості, важливі в тих чи інших алгоритмах: прямий (preorder), центрований (inorder) та зворотній (postorder).

Реалізація бінарних дерев

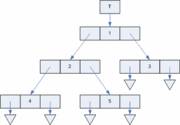
Реалізація бінарного дерева. Кожна вершина містить вказівники на праву та ліву дитину (left та right)

Існують декілька варіантів конструювання бінарних дерев в залежності від задач, які вирішуються цими структурами та можливостей тої чи іншої мови програмування. Реалізація з використанням вказівників передбачає зберігання в кожній вершині дерева x разом з даними двох полів з вказівниками (правим та лівим) right[x] та left[x] на відповідних дітей цієї вершини.

Модифікована реалізація бінарного дерева. Кожна вершина містить також вказівник на батьківську вершину

Також іноді додається вказівник p[x] на батьківську вершину. Це виявляється корисним, коли необхідний швидкий доступ до батьківської вершини та спрощує деякі алгоритми. Іноді достатньо тільки вказівника на батьківську вершину. Взагалі будь-яке орієнтоване дерево можна описати, знаючи тільки зв'язки від дітей до батьківської вершини. Деякі різновиди бінарних дерев (наприклад, червоно-чорні дерева або AVL-дерева), вимагають збереження в вершинах і деякої додаткової інформації. Якщо у вершини відсутня одна чи обидві дитини, відповідні вказівники ініціалізуються спеціальними "пустими" значеннями.

Бінарне дерево на базі масиву

Бінарні дерева також можуть бути побудовані на базі масивів. Такий метод набагато ефективніший щодо економії пам'яті. В такому представленні, якщо вершина має порядковий номер i, то її діти знаходяться за індексами 2i+1 та 2i+2, а батьківська вершина за індексом ((i-1)/2) (за умов, що коренева вершина має індекс 0). Інший варіант зберігання дерева в масиві — зберігати індекси дітей.

Представлення n-арних дерев як бінарних

Існує єдине та взаємооднозначне відображення довільного впорядкованого дерева в бінарне.

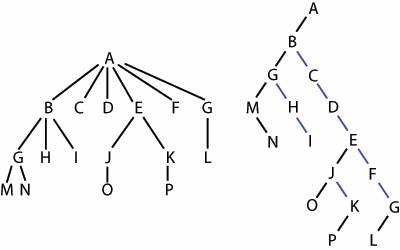
Для цього слід послідовно зв'язати усіх дітей кожної сім'ї з першою дитиною та та видалити усі вертикальні з'єднання за виключенням з'єднання батька з першою дитиною в сім'ї. Тобто кожна вершина N впорядкованого n-арного дерева відповідає вершині M деякого бінарного дерева. Ліва дитина вершини M відповідає першій дитині вершини N, а права дитина M відповідає першому з наступних братів N (тобто першому з наступних дітей батька вершини N).

Така відповідність має назву природної відповідності між n-арним та бінарним деревом.

Б) Бінарне дерево пошуку:

Бінáрне дéрево пóшуку (англ. binary search tree, BST) в інформатиці - бінарне дерево, в якому кожній вершині x співставлене певне значення val[x]. При цьому такі значення повинні задовольняти умові впорядкованості:

нехай x -- довільна вершина бінарного дерева пошуку. Якщо вершина y знаходиться в лівомі піддереві вершини x, то val[y] ≤ val[x]. Якщо у знаходиться у правому піддереві x, то val[y] ≥ val[x].

Таке структурування дозволяє надрукувати усі значення у зростаючому порядку за допомогою простого алгоритма центрованого обходу дерева. Бінарні дерева пошуку набагато ефективніші в операціях пошуку, аніж лінійні структури, в яких витрати часу на пошук пропорційні O(n), де n -- розмір масиву даних, тоді як в повному бінарному дереві цей час пропорційний в середньому O(log2n) або O(h), де h - висота дерева (хоча гарантувати, що h не перевищує log2n можна лише для збалансованих дерев, які є ефективнішими на пошукових алгоритмах, аніж прості бінарні дерева пошуку).

Пошук в бінарному дереві

Процедура пошуку в бінарному дереві отримує на вході значення k, яке необхідно знайти, та вказівник x на корень того піддерева, в якому слід шукати.

SEARCH (x, k)

1 if x = NULL or k = val[x]

2 then return x

3 if k < val[x]

4 then return SEARCH (left[x], k)

5 else return SEARCH (right[x], k)

В процесі пошуку ми рухаємось від кореня, порівнюючи значення k зі значенням в поточній вершині х. Якщо k < val[x], пошук рекурсивно продовжується в лівому піддереві (k може бути тільки там згідно умови впорядкованості), інакше -- у правому піддереві. Очевидно, що довжина шляху не перевищує висоти дерева, тому час пошуку є O(h), де h - висота дерева.

Мінімум, максимум, наступник та попередник

Мінімальний елемент в дереві можна знайти, розглянувши послідовно ліве піддерево left[x]:

MINIMUM (x)

1 while left[x]<>NULL

2 do x:=left[x]

3 return x

Процедура знаходження максимуму симетрична. Обидві процедури знову ж таки знаходять елемент за час, пропорційний O(h)

Елемент, що є наступним за даним (в сенсі відношення впорядкованості) можна знайти за допомогою такої процедури:

SUCCESSOR (x)

1 if right[x] <> NULL

2 then return MINIMUM (right[x])

3 y:=p[x]

4 while y<>NULL and x = right[y]

5 do x:=y

6 y:=p[y]

7 return y

Процедура знаходження попереднього даному елемента є симетричною. Обидві процедури знову ж таки знаходять елемент за час, пропорційний O(h)

Процедура додавання елементу в бінарне дерево T додає елемент, зберігаючи умову впорядкованості. Параметром тут є вказівник z на нову вершину, в яку поміщене значення val[z], left[z]=right[z]=NULL.

INSERT (T, z)

1 y:=NIL

2 x:=root[T]

3 while x <> NULL

4 do y:=x

5 if val[z] < val[x]

6 then x:=left[x]

7 else x:=right[x]

8 p[z]:=NULL

9 if y = NULL

10 then root[T]:=z

11 else if val[z]<val[y]

12 then left[y]:=z

13 else right[y]:=z

Процедура рухається вниз по дереву, при цьому зберігаючи в y вказівник на батька вершини x. Порівнюючи значення в x та z, процедура вирішує, в яке з піддерев рухатись далі. Процес завершується тоді, коли x=NULL. Саме сюди й слід помістити вершину z (рядки 8-13). Ця операція також потребує часу для виконання, пропорційного O(h)

Дата добавления: 2014-01-05