Нормальные напряжения при чистом изгибе

Согласно определению чистого изгиба, поперечная сила равна нулю в каждом сечении балки, поэтому M = const (поскольку 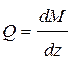). При чистом изгибе в поперечных сечениях балки возникают изгибающие моменты в плоскости, содержащей одну из главных центральных осей инерции.

Чтобы установить закон распределения внутренних сил, возникающих в поперечном сечении балки, уравнений статики недостаточно, необходимо рассмотреть геометрическую сторону задачи. Согласно гипотезе плоских сечений, поперечные сечения балки, плоские до деформации, рис. (а), остаются плоскими и после деформации, рис. (б).

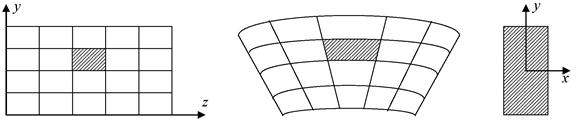
(а) (б)

Рис. 6.9

Деформацию изгиба можно представить как поворот сечений по дуге окружности радиусом ρ.

Рассмотрим два смежных сечения и выделим элемент длиною dz. Взаимный поворот смежных сечений на угол dθ.

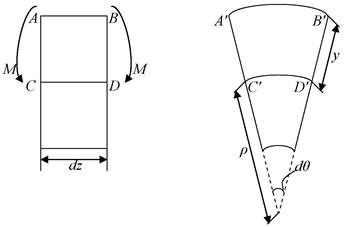
Рис. 6.10

В результате изгиба верхние слои балки удлинятся, нижние – укоротятся. Существует слой CD = C'D', длина которого не изменится. Положение слоя CD пока не известно. Выразим длину CD через угол dθ как элемент дуги окружности

.

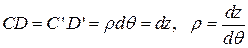Отрезок AB на расстоянии y от слоя CD удлинится на

.

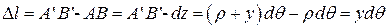Относительная деформация есть

.

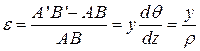Если принять справедливость гипотезы ненадавливания волокон, то продольные слои балки находятся в состоянии растяжения и сжатия. Переход к напряжениям осуществляется по закону Гука

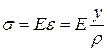. (6.1)

Здесь ρ – радиус кривизны нейтрального слоя.

Координата y отсчитывается от нейтрального слоя (нейтральной линии): вверх от нейтральной линии y > 0, вниз – y < 0. В соответствии с этим фактом в силу того, что E > 0, ρ > 0, напряжения σ будут либо положительными (растягивающими), либо отрицательными (сжимающими).

6.6 Связь между нормальным напряжением
и изгибающим моментом

Рассмотрим равновесие части балки, находящейся под действием внешнего изгибающего момента m и внутренних сил, возникающих в поперечном сечении балки. Начало координат в поперечном сечении поместим на нейтральной линии, рис. (а).

(а)

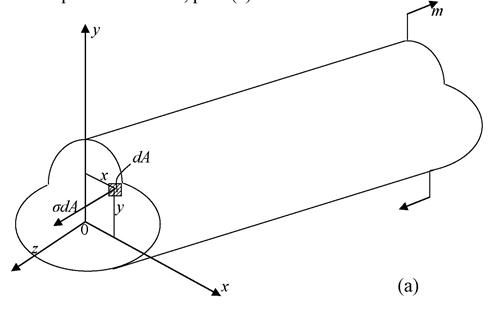
Рис. 6.11

Сумма элементарных нормальных сил 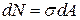, действующих по нормали от рассматриваемого сечения, есть интеграл по площади A:

.

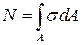Поскольку при чистом изгибе действует только момент m, продольная сила отсутствует, то

.

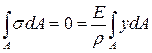Последний интеграл есть статический момент площади поперечного сечения балки S_x относительно оси x, которая совпадает с нейтральной линией. Так как 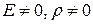, то

.

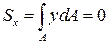Согласно теоремы Вариньона, статический момент равен нулю только в том случае, если ось координат проходит через центр тяжести поперечного сечения. Значит, положение нейтральной линии установлено: она проходит через центр тяжести поперечного сечения.

Найдем момент элементарных нормальных сил

.

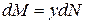Сумма моментов относительно оси х

.

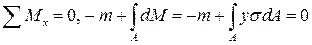На основании формулы (6.2) для нормальных напряжений получаем

.

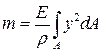Интеграл 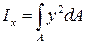представляет собой момент инерции сечения относительно оси x. На отсеченную часть балки может действовать не один момент m, а несколько. Тогда уравнение равновесия 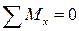будет содержать алгебраическую сумму моментов всех внешних сил, которая равна изгибающему моменту в рассматриваемом поперечном сечении. Следовательно,

,

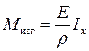откуда

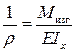. (6.2)

Величина 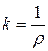представляет собой кривизну нейтрального слоя балки, 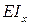- жесткость балки на изгиб.

Итак, кривизна оси балки при изгибе пропорциональна изгибающему моменту и обратно пропорциональна жесткости балки.

Учитывая (6.1), исключим ρ, тогда получим связь между нормальным напряжением σ и изгибающим моментом

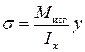. (6.3)

Формула (6.3) позволяет определить величину нормального напряжения в любой точке поперечного сечения балки по известным изгибающему моменту и моменту инерции сечения.

Формула (6.3) получена для чистого изгиба. При действии на балку поперечных сил в сечениях кроме нормальных возникают и касательные напряжения. Однако неучет поперечных сил в расчетах по (6.3) мало сказывается для балок, у которых отношение высоты к длине не превышает 5%.

Эпюра нормальных напряжений в поперечном сечении балки согласно (6.3) имеет вид

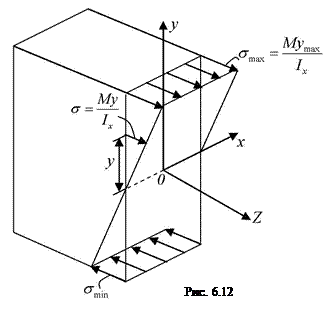Из эпюры видно, что внутрен­ние слои балки вблизи ней­тральной линии мало напря­жены. Для экономии мате­риала площадь сечения необ­ходимо распределять по­дальше от нейтральной линии, то есть использовать сечения с большими моментами инерции относительно нейтральной ли­нии. Наиболее рациональным оказывается применение про­катных профилей (двутавров, швеллеров и т.п.), рис. 6.13.

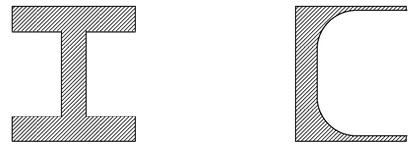
(а) (б)

Рис. 6.13

Дата добавления: 2014-01-05