Правило знаков для Q, M

Знаки перерезывающей силы Q и изгибающего момента M зависят от того, какая часть балки рассматривается: правая или левая. Поперечная сила в сечении положительна, если равнодействующая внешних сил слева от сечения направлена снизу-вверх, справа от сечения – сверху-вниз, и отрицательная в противном случае.

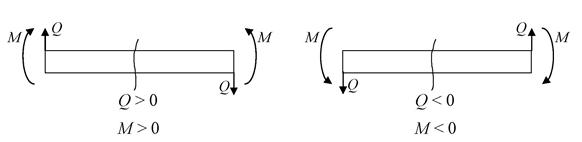
Рис. 6.6

Изгибающий момент положителен, если равнодействующая внешних моментов изгибает балку выпуклостью вниз; изгибающий момент отрицателен, если изгиб происходит выпуклостью вверх.

Рис. 6.7

6.4 Зависимость между изгибающим моментом, поперечной силой
и интенсивностью погонной нагрузки (теоремы Журавского)

Рассмотрим балку, нагруженную произвольной нагрузкой, рис 6.8.

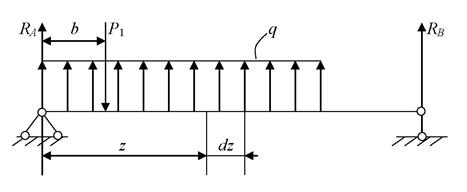
Рис. 6.8

Определим поперечную силу в сечении, отстоящем от левой опоры на расстоянии z. Проецируя на вертикаль силы, расположенные левее сечения, получим

.

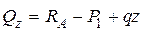Аналогично для сечения z + dz имеем

.

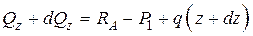Вычитая из второго уравнения первое, получаем

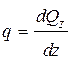. (а)

Таким образом, производная от поперечной силы по продольной координате равна интенсивности погонной нагрузки (первая теорема Журавского).

Вычислим изгибающий момент в сечении с абсциссой z. Распределенную нагрузку на участке длиной z заменим ее равнодействующей, равной qz и приложенной к середине участка, на расстоянии z /2 от сечения.

.

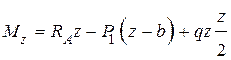Изгибающий момент в сечении z + dz

.

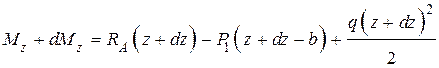Разность двух последних уравнений есть (пренебрегаем слагаемым )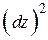

.

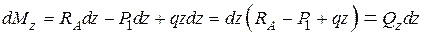Следовательно,

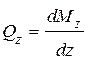. (б)

Производная от изгибающего момента по продольной координате равна поперечной силе (вторая теорема Журавского).

Из (а) и (б) следует

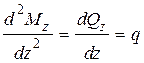. (в)

Полученные зависимости используются при построении эпюр изгибающих моментов и поперечных сил.

Из зависимостей (а) – (в) вытекают правила, которые определяют характер эпюр Q, M и применяют для контроля правильности их расчета.

1. Если на участке отсутствует погонная нагрузка, q = 0, то эпюра Q – прямая, параллельная оси z, эпюра M – наклонная прямая.

2. На участке с равномерно распределенной нагрузкой q = const, эпюра Q представляет наклонную прямую, эпюра M – параболу, направленную выпуклостью навстречу направлению действия q.

3. На участках, где Q > 0, изгибающий момент возрастает; если Q < 0, то изгибающий момент убывает (в случае правосторонней системы координат). Если Q = 0, то изгибающий момент постоянен.

4. Если перерезывающая сила пересекает ось z, Q = 0, то в данном сечении момент имеет максимум, если Q меняет знак с плюса на минус; минимум в противоположном случае (величина Q проходит через нулевое значение, меняя знак с минуса на плюс).

Дата добавления: 2014-01-05