Метод начальных параметров

Для решения дифференциального уравнения (6.8) воспользуемся методом начальных параметров.

Рассмотрим балку, нагруженную взаимоуравновешенной системой нагрузок, рис. 6.18.

Рис. 6.18

Будем рассматривать все участки балки в единой системе координат, помещая начало в крайнее левое, либо в крайнее правое сечение. Рассмотрим особенности, вносимые в уравнение упругой линии различными видами внешних нагрузок. Уравнения моментов по участкам будут следующими

1.

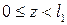
2.

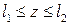
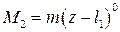
3.

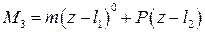
4.

5.

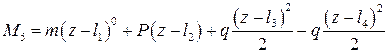
Заметим, что все моменты в 1-5 положительны.

В целях формализации процедуры интегрирования уравнения моментов по участкам имеют следующие особенности:

а) слагаемые, содержащие сосредоточенный момент m, умножены на , где - координата приложения m;

б) все распределенные нагрузки (в примере это нагрузка, приложенная в сечении и снятая в сечении 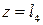) продлеваются до конца балки;

в) в сечениях, где распределенная нагрузка отсутствует, но есть продленная, прикладывается компенсирующая нагрузка.

Уравнения моментов по участкам можно объединить в универсальное уравнение момента

(6.9)

Вертикальная черта и условие указывает на равенство нулю соответствующего слагаемого в случае, когда неравенство не выполнено. Например, первое слагаемое 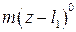отсутствует в , если . Интегрирование (6.9) дает универсальное уравнение углов поворота

. (6.10)

Повторное интегрирование дает универсальное уравнение прогибов

. (6.11)

Применение универсального уравнения позволяет значительно упростить решение, особенно для балок с несколькими участками.

Правила проверки правильности построения изогнутой оси балки основаны на связи изгибающего момента и кривизны балки

,

где ρ – радиус кривизны в сечении:

1) на участке, где изгибающий момент положителен, ось балки изогнута выпуклостью вниз;

2) на участке, где изгибающий момент отрицателен, ось балки изогнута выпуклостью вверх;

3) на участке, где M = 0, ось балки прямая линия;

4) в сечении где M = 0, у изогнутой оси балки – точка перегиба.

Дата добавления: 2014-01-05