
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Плоское напряженное состояние
|
|
|
|
Анализируя плоское напряженное состояние, установим связь между главными напряжениями и напряжениями, действующими на наклонных площадках (рис. 7.4, а).

а) б) в)
Рис.7.4
Поскольку здесь два отличных от нуля напряжения, условимся отсчитывать угол наклона площадки  от большего из двух напряжений (рис.7.4,б).
от большего из двух напряжений (рис.7.4,б).
Применяя принцип суперпозиции, будем рассматривать данное напряженное состояние как наложение двух ортогональных одноосных напряженных состояний (рис 7.4, б, 7.4, в). В соответствии с принятым:
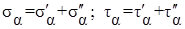 . (7.5)
. (7.5)
При вычислении напряжений воспользуемся непосредственно формулами (7.3) и (7.4). Нормаль n составляет с направлением 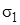 угол
угол  , с направлением
, с направлением 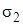 – угол
– угол  . Вычисляя, получим:
. Вычисляя, получим:
 (7.6)
(7.6)
 (7.7)
(7.7)
Определим напряжения на площадке 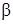 , перпендикулярной к площадке
, перпендикулярной к площадке 
 ; (7.8)
; (7.8)
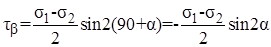 . (7.9)
. (7.9)

Рис.7.5
Сравнивая формулы (7.7) и (7.9),замечаем, что 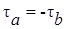 . Касательные напряжения на взаимно перпендикулярных площадках равны по величине и противоположны по знаку, что выражает закон парности касательных напряжений.
. Касательные напряжения на взаимно перпендикулярных площадках равны по величине и противоположны по знаку, что выражает закон парности касательных напряжений.
Условимся считать касательное напряжение положительным, если оно стремится повернуть элемент по часовой стрелке.
Нормальные напряжения положительны, если они совпадают по направлению с положительной нормалью к грани элемента.
Суммируя левые и правые части уравнений (7.6) и (7.8), обнаруживаем, что
 ,
,
т.е. сумма нормальных напряжений на взаимно перпендикулярных площадках есть величина постоянная.
Проведя соответствующие исследования, замечаем, что касательные напряжения достигают экстремального значения на площадках расположенных под углом 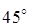 к главным.
к главным.
Нормальные напряжения экстремальны на главных площадках.
Таким образом, для практических расчетов более важной задачей является определение главных напряжений.
В том случае, когда известны нормальные и касательные напряжения, действующие на двух взаимно перпендикулярных площадках, аналитические выражения для определения главных напряжений имеют вид:
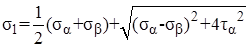 ; (7.10)
; (7.10)
 . (7.11)
. (7.11)
Если одно из вычисленных главных напряжений окажется положительным, а другое отрицательным их следует обозначать 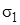 и
и 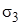 соответственно. Если отрицательны оба главных напряжения, то меньшее по модулю напряжение следует обозначить
соответственно. Если отрицательны оба главных напряжения, то меньшее по модулю напряжение следует обозначить 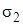 , а большее
, а большее 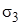 .
.
Величины главных напряжений и положение главных площадок можно определить и графически, построив для этого, так называемый, круг напряжений, или круг Мора.
Построение круга напряжений ведут в системе отсчета 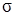 и
и 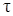 .
.
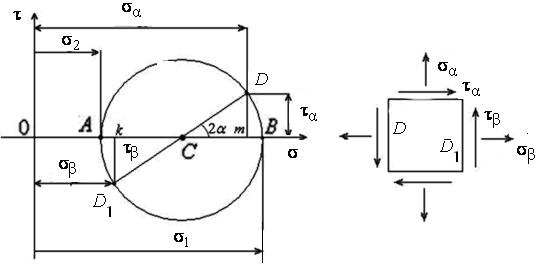
Рис 7.6
Ось 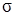 – направлена по горизонтали,
– направлена по горизонтали, 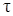 – по вертикали.
– по вертикали.
Каждая точка круга напряжений представляет одну из площадок, характеризуемых определенными значениями 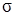 и
и 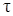 .
.
1. Строим точку D круга, откладывая 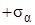 и
и  в соответствии с оговоренными ранее правилами знаков. Точка D соответствует площадке
в соответствии с оговоренными ранее правилами знаков. Точка D соответствует площадке  . Точка
. Точка 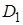 с координатами
с координатами 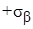 ,
, 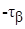 представляет площадку
представляет площадку 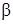 .
.
2. Соединяем точки D и 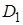 прямой. В пересечении с горизонтальной осью
прямой. В пересечении с горизонтальной осью 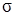 получается центр круга напряжений C.
получается центр круга напряжений C.
3. Радиусом CD=C 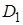 проводим окружность
проводим окружность
4. Точки A и B представляют главные площадки, т.к. координаты 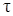 этих точек равны нулю, а
этих точек равны нулю, а 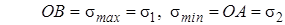
Отрезки OB и OA могут быть представлены в виде OB=OC+CB, OA=OC-CA. Поскольку радиусы круга CB=CD, СA=CD, можно записать
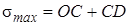 , (7.12)
, (7.12)
 . (7.13)
. (7.13)
Как легко увидеть OC=OK+KC, где 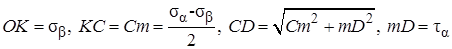 .
.
Подставляя полученное в (7.12) и (7.13) запишем
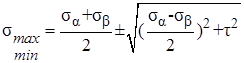 , (7.14)
, (7.14)
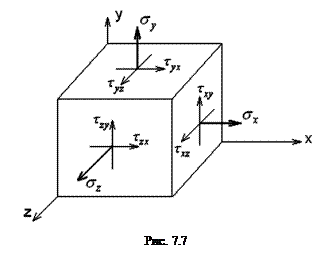 что полностью соответствует аналитическим соотношениям (7.10), (7.11). В общем случае напряженное состояние в точке характеризуется девятью компонентами. Три из них σx, σy, σz –нормальные напряжения,
что полностью соответствует аналитическим соотношениям (7.10), (7.11). В общем случае напряженное состояние в точке характеризуется девятью компонентами. Три из них σx, σy, σz –нормальные напряжения,
шесть остальных – касательные напряжения с двумя индексами: первый соответствует нормали к площадке, второй – направлению оси параллельной рассматриваемому τ. Эта совокупность напряжений называется тензором напряжений. Изменяя направление секущих плоскостей можно выйти на главные площадки, где касательные напряжения равны нулю, а нормальные достигают экстремальных значений
Определение положения главных площадок и направления действия главных напряжений позволяет профессионально создавать железобетонные конструкции. Именно в направлении действия главных напряжений укладывают металлические стержни в железобетонной балке, повышая ее прочность и жесткость.
7.3 Деформации при объемном напряженном состоянии.
Обобщенный закон Гука
Изучая осевое растяжение, мы выяснили, что относительная продольная деформация связана с напряжением:
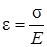 , (7.15)
, (7.15)
а относительная поперечная деформация с продольной
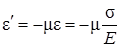 . (7.16)
. (7.16)
Рассмотрим деформацию элемента тела размерами a,b,c по граням которого действуют главные напряжения 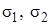 и
и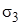 .
.
 Деформацию в направлении
Деформацию в направлении 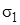 от
от 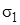 обозначим
обозначим  .
.
Деформация в направлении 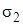 от
от 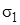 равна
равна 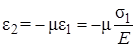 Деформация в направлении
Деформация в направлении 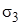 от
от 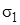 ,равна
,равна 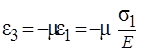 .
.
Аналогично могут быть определены деформации и в направлении действия двух других главных напряжений.
Сведем расчетные соотношения в таблицу.
Таблица 7.1
 В напр. От В напр. От
| 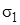
| 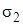
| 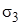
|
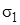
| 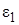
| 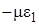
| 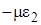
|
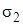
| 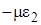
| 
| 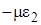
|
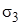
| 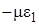
| 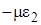
| 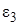
|
Выражая полную деформацию, получаем
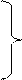 в направлении действия
в направлении действия 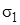
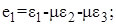
в направлении действия 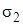
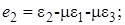 (7.17)
(7.17)
в направлении действия 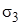
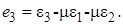
Воспользовавшись соотношением (7.15), получаем обобщенный закон Гука при трехосном напряженном состоянии:
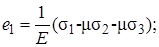
 (7.18)
(7.18)
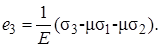
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 495; Нарушение авторских прав?; Мы поможем в написании вашей работы!