
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Робота з Меню програми
|
|
|
|
Тест
Тест
Витрати на рекламу в INTERNET, тис грн.
Витрати на рекламу, тис. грн.
Прибуток млн. грн.
Прибуток тис. грн.
Обсяг виробництва, млн. грн.
2003 4500 3200 2890 3800 2100 6300 4100
Варіант №5
Товарообіг тис. грн.
20 30 56 23 50 90 78 89 78 80
Варіант №6
Товарні запаси тис. грн.
230 456 560 230 780 560 120 230 890 820
Варіант №7
Товарообіг, тис. грн.
230 560 890 450 120 650 890 560 180 200 900 960
Варіант №8
46 120 189 90 23 123 230 110 130 191
Варіант №9
456 560 562 650 658 780 782 795 810 820
Варіант №10
23,6 25,23 24,6 26 26,8 32,6 32,8 35,3 37 36
Варіант №11
Валові витрати, тис. грн.
8 9,6 12 8 8,6 10 12 20 22 22,6
Варіант №12
Фондовіддача, тис. грн..
23 43 23 32 62 64 68 65 68 70
Варіант №13
Виробництво продукції на одного працюючого, тис. грн.
90 92 100 110 120 320 456 890 789 700
Варіант №14
Обсяг реалізації продукції через INTERNET, тис грн.
232 542 652 560 952 953 1000 980 996 1000
Варіант №15
12,3 14,5 15,6 14,8 15,9 17,9 18 17,9 18,3 19
| Питання | Варіанти відповідей | ||||
| 1. Які існують моделі рядів динаміки фінансово-економічних показників? | a. Оптимізаційна. b. Адитивна. c. Мультиплікативна. | ||||
| 2. Дайте визначення тренда фінансово-економічних показників? | a. Це функція, що визначає основну тенденцію розвитку значень фінансово-економічного показника в часі. b. Це зміни значень показника, які відбуваються протягом одного періоду й повторюються кожний період. c. Це трендова функція розвитку фінансово-економічного показника. | ||||
| 3. Для здійснення перевірки ряду динаміки на наявність тренду показник мусить складатись не менш ніж | a. 12 періодів. b. 10 періодів. c. 6 періодів. d. 22 періодів. | ||||
| 4. Установіть відповідність використання певної функції: | |||||
| a. 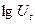 - лінійно змінюються
b. - лінійно змінюються
b.  - приблизно дорівнюють const
c. - приблизно дорівнюють const
c.  - лінійно змінюються, - лінійно змінюються,  - приблизно дорівнюють const.
d. - приблизно дорівнюють const.
d.  - приблизно дорівнюють const. - приблизно дорівнюють const.
| ||||
| 5. За допомогою якого показника можна перевірити вірогідність побудованої трендової моделі? | a. Коефіцієнта детермінації (R2).
b. Коефіцієнта варіації V.
c. Темпу приросту 
| ||||
| 6. У яких випадках можна вважати, що функція є достовірною? | a. 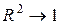 b.
b. 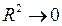 c.
c. 
| ||||
| 7. Для різних показників проведена перевірка існування тренда методом істотності різниці середніх. Виберіть варіанти, коли можна вважати, що тренд існує. | a. t – розрахункове становить –0,058,  - 3,05.
b. t – розрахункове становить –0,03, - 3,05.
b. t – розрахункове становить –0,03,  - 1,07.
c. t – розрахункове становить –1,23, - 1,07.
c. t – розрахункове становить –1,23,  - 0,05. - 0,05.
| ||||
| 8. За допомогою якої дії викликається інструменти для проведення тестів на існування тренду? | a. Сервис/Анализ данных b. Сервис/Поиск решения c. Сервис/Анализ данных/вибрати необхідний інструмент аналізу. | ||||
| 9. Які дії необхідно виконати для додавання лінії тренда на діаграму? | a. Вибрати команду: Добавить линию тренда із контекстного меню. b. Щелчок правої кнопки миші по ряду диаграми. Вибрати команду: Добавить линию тренда із контекстного меню. | ||||
| 10. Чи є функція у=2,263х2+5,94х+10,27 з показником R2=0,3593 достовірною? | a. Так. b. Ні. | ||||
3 Інформаційні технології багатофакторного аналізу в системі обробки економічної інформації засобами пакета Microsoft Excel
3.1 Методологія багатофакторного аналізу в системі обробки економічної інформації
Кількісний облік і обробка економічної інформації залежить від цілей дослідження й від поставлених завдань. Рішення завдання оцінки функціональних залежностей в економічній предметній області дає можливість системі управління приймати адекватні рішення з оптимізації економічних процесів досліджуваної предметної області. Одним з методів рішення наведеного вище завдання є виявлення та побудова багатофакторних функціональних залежностей, тобто проведення кореляційно-регресійного аналізу.
Кореляційно-регресійний аналіз у системі обробки економічної інформації використовується для вивчення й моделювання зв’язків між економічними показниками.
У цьому випадку аналізу підлягають наступні предметні області фінансової спеціалізації: аналіз потоків платежів, розробка планів погашення кредитів, аналіз ефективності інвестиційних проектів, аналіз ризиків, аналіз фінансових операцій та ін.
Економічні показники по їхньому значенню можна розділити на два класи: факторні й результативні.
Результативний показник (y) – досліджуваний показник, що характеризує ефективність економічного процесу.
Факторний показник (x) – показник, що робить вплив на результативний показник.
По ступені або рівню детермінованості бувають стохастичні й функціональні зв’язки.
Стохастичні зв’язки між економічними показниками виникають у випадках ймовірних процесів.
Під детермінованістю в цьому випадку передбачається наявність твердого функціонального зв’язку між змінними.
Приватним випадком функціонального зв’язку є кореляційний зв’язок.
Зв’язок між показниками є кореляційним, якщо закон розподілу однієї величини відповідає закону розподілу інший, або, якщо зміна математичного очікування однієї величини спричиняє зміну математичного очікування іншої.
Для кількісної оцінки щільності зв’язку широко використовується лінійний коефіцієнт кореляції. Лінійний коефіцієнт кореляції змінюється в межах від -1 до +1. Інтерпретація вихідних значень коефіцієнта кореляції представлена в табл. 3.1.
Таблиця 3.1 – Оцінка лінійного коефіцієнту кореляції r
| Тіснота зв’язку | Прямий зв’язок | Зворотній зв’язок |
| Слабкий | 0,1-0,3 | (-0,1)- (-0,3) |
| Помірний | 0,3-0,5 | (-0,3)- (-0,5) |
| Значний | 0,5-0,7 | (-0,5)- (-0,7) |
| Високий | 0,7-0,9 | (-0,7)- (-0,9) |
| Вельми високий | 0,9-0,99 | (-0,9)- (-0,99) |
Регресійна модель – запис виявленого зв’язку між результативним показником і факторами у вигляді рівняння, коли результуючий показник має випадкову складову, а фактори – детерміновані.
Теоретичною лінією регресії називається лінія, навколо якої групуються крапки кореляційного поля і яка вказує на основну тенденцію зв’язку.
По напрямку зв’язки розрізняють:
- пряма регресія – виникає за умови, якщо зі збільшенням або зменшенням незалежного показника значення залежного показника відповідно збільшується або зменшується;
- зворотна регресія – виникає за умови, якщо зі збільшенням або зменшенням незалежного показника значення залежного показника відповідно зменшується або збільшується.
Регресійний аналіз часто обмежується простим зв’язком між одним факторним і результативним показниками. Але у випадках, коли дуже важко встановити закономірний зв’язок стає необхідним використання множинної регресії.
Таким чином, однією із проблем побудови регресійної моделі є її розмірність, тобто визначення числа факторних показників, що включаються в модель. Їхнє число повинне бути оптимальним. Скорочення розмірності за рахунок виключення другорядних факторів дозволяє одержати більше якісну модель. У той же час побудова моделі малої розмірності може привести до того, що вона буде недостатньо точною.
3.2 Відбір факторів для проведення аналізу
Для вирішення проблеми визначення числа факторних ознак, що включаються в модель можливе скорочення розмірності за рахунок виключення другорядних факторів. Але тоді виникає проблема точності моделі, що описує об’єкт. Практика виробила певний критерій, що дозволяє встановити оптимальне співвідношення між числом факторних показників, що включаються в модель, і обсягом досліджуваної сукупності. Відповідно до даного критерію число факторних ознак повинне бути в 5 разів менше обсягу досліджуваної сукупності.
Складність і взаємне переплетення окремих факторів, що обумовлюють досліджуване економічне явище, можуть проявлятися в мультиколінеарності.
Мультиколінеарність – тісний зв’язок факторів між собою в економічних процесах, описуваних багатофакторними залежностями.
Наявність мультиколінеарності між факторами приводить до наступних негативних наслідків:
1. Перекручуванню величини параметрів моделі, які мають тенденцію до завищення.
2. Зміні змісту економічної інтерпретації коефіцієнтів регресії.
3. Ускладненню процесів визначення найбільш істотних факторних ознак.
Причинами виникнення мультиколінеарності між факторами можуть бути:
1. Факторні ознаки характеризують ту саму сторону процесу, наприклад, не рекомендується включати одночасно в модель показники обсягу виробленої продукції й середньорічної вартості основних фондів, тому що вони обидва характеризують розмір підприємства.
2. Використання у якості факторних ознак таких показників, сумарне значення яких являє собою майже постійну величину.
3. Факторні ознаки, що представляють собою складені елементи один одного.
4. Факторні ознаки, за економічним змістом дублюючі один одного.
Для усунення мультиколінеарності факторів процесу що моделюється необхідно виконати перевірку виконання наступних вимог:
1. Дотримання незалежності по об’єктах спостережень.
2. Факторні й результативні показники повинні відповідати нормальному закону розподілу:
 , (3.1)
, (3.1)
де:  - мінімальне й максимальне значення показника відповідно,
- мінімальне й максимальне значення показника відповідно,
 - величина середнього значення показника,
- величина середнього значення показника,
 - середньоквадратичне відхилення показника.
- середньоквадратичне відхилення показника.
Вираз (3.1) є законом 3-х сигм.
3. Повинна дотримуватися статистична однорідність факторних показників і результативного, тобто мінливість показників стосовно свого середнього значення не повинна бути занадто високою. Виконання даної вимоги перевіряється за допомогою коефіцієнта варіації Vy. Коефіцієнти варіації показників не повинні перевищувати 33%:
 . (3.2)
. (3.2)
4. Між факторними показниками не повинно бути функціонально щільного кореляційного зв’язку. Це означає, що парний коефіцієнт кореляції не повинен перевищувати за модулем (0,7 - 0,8):
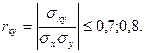 (3.3)
(3.3)
де:  - середнє квадратичне відхилення між факторним і результативним показниками,
- середнє квадратичне відхилення між факторним і результативним показниками,
 - середнє квадратичне відхилення факторного показника,
- середнє квадратичне відхилення факторного показника,
 - середнє квадратичне відхилення результативного показника.
- середнє квадратичне відхилення результативного показника.
Щоб усунути мультиколінеарність, необхідно виключити з моделі одну або декілька лінійно зв’язаних факторних ознак, або перетворити вихідні факторні ознаки в нові, укрупнивши їх. Питання про те, який з факторів варто відкинути, зважується на основі якісного й логічного аналізів досліджуваних фінансово-економічних показників. Рішення щодо усунення або заміни фактора може бути прийнято експертним шляхом.
3.3 Визначення регресійної функції. Оцінка якості регресійної моделі
Для визначення типу регресійної функції проводиться аналіз емпіричних даних по наступних напрямках:
1. Визначення напрямку зв’язку.
2. Визначення зміни напрямку зв’язку досліджуваної сукупності (чи є залежність монотонною).
3. Визначення характеру змін: рівномірно прискорюваних або що вповільнюються (лінійного або нелінійного характеру).
Необхідні, для визначення типу функції, відомості одержують із емпіричного матеріалу. Висновок про напрямок і форму зв’язку (аналітичному вираженню) можна одержати шляхом паралельного порівняння рядів показників, а також із графічного аналізу.
У наступній таблиці наведені типи функцій, що використовуються найбільше часто для опису парних та багатофакторних залежностей.
У таблиці прийняті наступні позначення:
а0 – довільний член регресії,
а1 – коефіцієнт регресії.
Таблиця 3.2 – Типи регресійних функцій
| Найменування | Функція | Випадок використання |
| Лінійна |  , ,
| X і Y зростають приблизно в арифметичній прогресії. |
| Гіперболічна |  , ,
| Зв’язок між X і Y зворотний. |
| Показова |  , ,
| Логарифми Х зростають приблизно в арифметичній прогресії. |
| Параболічна | 
| X збільшується в арифметичній прогресії, а Y значно швидше. |
| Ступенева | 
| |
| Логістична | 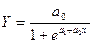
| Відношення приростів логарифмів Х є постійною величиною. |
З наведених форм зв’язку вибирають за формальними критеріями апроксимації одну. Для цього рекомендується використовувати один із двох критеріїв, що характеризують середню помилку апроксимації функції:
1. Показник середньої помилки апроксимації:

 ,
,
 де: n – число значень досліджуваного показника,
де: n – число значень досліджуваного показника,

 - i – е значення досліджуваного показника,
- i – е значення досліджуваного показника,

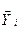 - вирівняне по функції i – е значення досліджуваного показника.
- вирівняне по функції i – е значення досліджуваного показника.
2.  Показник середньої квадратичної помилки:
Показник середньої квадратичної помилки:
 ,
,
де: k – число факторних ознак.
Застосування зазначених критеріїв є досить надійним способом відбору адекватних математичних моделей, при цьому значення помилки апроксимації не повинне перевищувати 12% - 15%.
Вірогідність побудованої регресійної моделі можна перевірити за допомогою коефіцієнта детермінації (R2):
 ,
,  , (3.4)
, (3.4)
де  - значення параметра Y, розраховане відповідно до регресійної моделі.
- значення параметра Y, розраховане відповідно до регресійної моделі.
Коефіцієнт детермінації показує якою мірою варіація результативного показника обумовлена впливом факторних показників.
Якщо 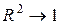 , то лінія регресії точно відповідає всім спостереженням.
, то лінія регресії точно відповідає всім спостереженням.
Коли можна стверджувати, що видимий зв’язок між X і Y є відсутній.
можна стверджувати, що видимий зв’язок між X і Y є відсутній.
Якщо R2 має нечітко виражене граничне значення (наприклад, 0.5), то в таких випадках зручно використовувати критерій Фішера або F - Тест.
При проведенні F - Тесту будемо вважати нульовою гіпотезою те, що значення R2 отримане випадково й між величинами немає зв’язку.
Порядок перевірки моделі на адекватність за критерієм Фішера такий:
1. Розрахунок величини F - відносини:
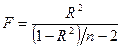 (3.5)
(3.5)
2. Вибір користувачем рівня значимості  =0,05 або
=0,05 або  =0,01.
=0,01.
3. По статистичних таблицях F - розподілу знаходимо граничне значення Fкр при v1=(k-1) і v2=(n-k) ступенях волі.
Якщо розраховане значення 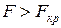 , то відкидається нульова гіпотеза з ризиком помилки не більше, ніж у
, то відкидається нульова гіпотеза з ризиком помилки не більше, ніж у  випадків.
випадків.
Потім провадитися оцінка значимості коефіцієнтів регресії за допомогою t-критерію Ст’юдента:
 . (3.6)
. (3.6)
Параметр моделі зізнається статистично значимим, якщо 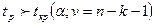 ,
,
де  - рівень значимості критерію перевірки гіпотези про рівність нулю параметрів, що вимірюють зв’язок (задається користувачем),
- рівень значимості критерію перевірки гіпотези про рівність нулю параметрів, що вимірюють зв’язок (задається користувачем),
 - число ступенів волі, що характеризує число вільно елементів сукупності, що варіюють.
- число ступенів волі, що характеризує число вільно елементів сукупності, що варіюють.
Після оцінки значимості всіх коефіцієнтів регресії з моделі виключається той фактор, коефіцієнт при якому є не значимим й має найменше значення критерію.
Таким чином, при виборі кращої регресійної моделі варто керуватися такими принципами:
1. Модель повинна бути адекватною за F - критерієм Фішера.
2. Коефіцієнти регресії повинні бути статистично значимі (задовольняти t - критерію Ст’юдента).
3. Обрана математична функція повинна мати мінімальну помилку апроксимації серед всіх розглянутих рівнянь регресії.
При цьому можливі наступні варіанти:
1. Побудована модель на основі перевірки за F - критерієм Фішера адекватна, і всі її коефіцієнти значимі. Така модель може бути використана для прийняття рішень і здійснення прогнозів.
2. Модель за F - критерієм Фішера адекватна, але частина коефіцієнтів регресії незначима. У цьому випадку модель придатна для прийняття рішень, але не повинна використовуватися для прогнозування. Використання моделі для прогнозування можливо після виключення факторів, коефіцієнти яких є незначимі.
3. Модель за F - критерієм Фішера адекватна, але всі коефіцієнти регресії є незначимі. Така модель повністю вважається неадекватною.
Параметри рівняння регресії розраховуються за методом найменших квадратів.
аi - параметр, що показує на скільки одиниць свого виміру зміниться Y, якщо xi збільшитися на одну одиницю свого виміру, за умови, що всі інші фактори, включені в модель, впливають на Y, але не варіюють, тобто зафіксовані на рівні свого середнього значення.
а0 – параметр, що виражає сукупний вплив всіх неврахованих факторів, його внесок у значення результуючого показника не залежить від зміни факторів.
По параметрах рівняння можна оцінити частку кожного з факторів у зміні рівня результативного показника. Це може бути зроблено шляхом прямої оцінки за величиною коефіцієнтів регресії, а так само і за коефіцієнтом еластичності:
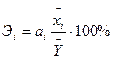 . (3.7)
. (3.7)
Коефіцієнт еластичності показує, на скільки відсотків зміниться результативний показник при зміні факторного показника на один відсоток при фіксованому положенні інших факторів.
Чим більше величина коефіцієнта регресії, тим значніше вплив даного показника на результуючий. Особливе значення при цьому має знак перед коефіцієнтом регресії.
Знаки говорять про характер впливу на результативний показник. Якщо факторний показник має знак плюс, то зі збільшенням даного фактору результативний показник зростає; якщо факторний показник має знак мінус, то з його збільшенням результативний показник зменшується.
3.4 Приклад проведення багатофакторного аналізу засобами пакета Microsoft Excel
Побудуємо двофакторну лінійну регресійну модель за даними, наведеним у табл. 3.3 і проведемо її аналіз.
У табл. 3.3 представлені дані про прибуток умовного торговельного підприємства за 12 періодів. Потрібно виявити залежність показника прибутку Y від показників обсягу реалізації x1 і витрат на рекламу x2.
Таблиця 3.3 – Статистичний зв’язок між показниками прибутку, обсягом реалізації продукції і витратами на рекламу
| № п/ч | Обсяг реалізації продукції (тис.грн.) x1 | Витрати на рекламу (тис.грн.) | Прибуток (тис.грн.) Y |
| 2,2 | |||
| 4,3 | |||
| 4,8 | |||
| 7,8 | |||
| 7,9 | |||
| 8,2 | |||
| 8,3 | |||
| 8,7 | |||
| 9,2 | |||
| 9,3 | |||
| 9,5 |
На підставі даних наведених у табл. 3.3 виконаємо аналіз наявності у вхідних даних причинно-наслідкових зв’язків факторних показників із результативним показником.
Регресійну двофакторну модель побудуємо у лінійній формі і перевіримо її на адекватність.
У даній функції факторними показниками є показник обсягів реалізації продукції (x1) і показник витрат на рекламу (x2), результативним показником є показник прибутку (Y).
Першим кроком аналізу є формування таблиці зі вхідними показниками як це показано на рис. 3.1.
Зробимо перевірку факторів на виконання статистичних вимог наведених вище.
1. Факторні й результативні показники повинні відповідати нормальному закону розподілу.
Вхідні дані формуються по стовпцях.
Виконати команду Сервис – Анализ данних – Описательная статистика.
Заповнити вікно діалогу за зразком (рис. 3.1):

Рисунок 3.1- Вікно діалогу «Описательная статистика»
У якості вхідного інтервалу виділяємо таблицю з найменуваннями стовпців (В2:D14), обов’язково встановлюємо прапорець «Метки в первой строке». Excel використовує ці мітки для створення заголовків у вихідній таблиці. Виділяємо прапорець «Итоговая статистика».
Після натискання кнопки ОК, будуть отримані наступні результати, як показано на рис.3.2.

Рисунок 3.2 – Описова статистика показників
За результатами описової статистики для аналізу будуть використовуватися наступні показники:
1. Середнє значення – являє собою координату показника, щодо якої групуються всі значення ряду даних.
2. Стандартне відхилення – являє собою позитивне значення кореня квадратного з дисперсії показника.
3. Мінімальне значення – являє собою найменше значення показника.
4. Максимальне значення – являє собою найбільше значення показника.
У відповідність із законом 3-х сигм (формула 3.1) зробимо перевірку показників на відповідність нормальному закону розподілу.
Для цього необхідно в чарунку В16 за допомогою функції ЕСЛИ ввести формулу (3.1):
=ЕСЛИ(И(B12>=B3-3*B7;B13<=B3+3*B7);"розподіл нормальний";"розподіл інший").
Заповнити вікно діалогу за зразком (рис. 3.3):
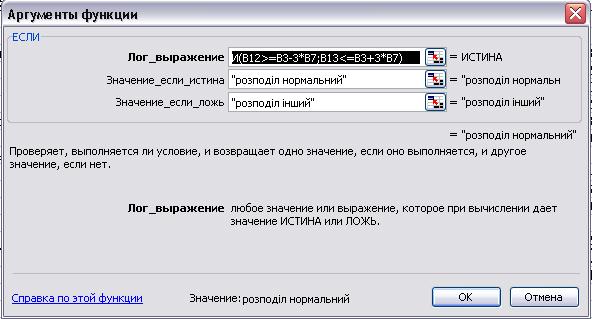
Рисунок 3.3- Вікно функції ЕСЛИ
В чарунки D16, F16 скопіювати вираження чарунки В16. Як видно з рис.2.12 всі фактори мають нормальний закон розподілу, та можуть бути використані для побудови регресійної моделі.
2. Повинна дотримуватися статистична однорідність факторних показників і результативного. Виконання даної вимоги перевіряється за допомогою коефіцієнта варіації Vy. Коефіцієнти варіації показників не повинні перевищувати 33%.
Для перевірки даної умови необхідно ввести в чарунку В17 формулу (3.2): =B7/B3, потім скопіювати вираження в чарунки D17 і F18 та встановити відсотковий формат цих чарунок. Як видно з рис. 3.2 статистична однорідність дотримується для всіх показників. Це означає, що результати моделювання будуть досить точними.
3. Між факторними показниками не повинно бути функціонально щільного кореляційного зв’язку. Це означає, що парний коефіцієнт кореляції не повинен перевищувати за модулем приблизно 0,7 – 0,8.
Для перевірки даної умови необхідно виконати команду Сервис – Анализ данних – Корреляция. Заповнити вікно діалогу за зразком:

Рисунок 3.4- Вікно діалогу «Корреляция»
У результаті виконання даного діалогу будуть отримані наступні результати (рис.3.5)

Рисунок 3.5- Коефіцієнти кореляції
Як видно з рис. 3.5 між факторними показниками коефіцієнт кореляції склав - 0,95. Даний показник є зависоким, це означає, що між факторами може бути функціональний зв’язок. Але з приводу того, що у прикладі аналізується вплив всього двох факторів на результативний показник, то ці фактори можуть бути використані для побудови регресійної моделі.
Для побудови регресійної моделі необхідно виконати наступні команди: Сервис – Анализ данних – Регрессия. Заповнити вікно діалогу за зразком (рис.3.6.):
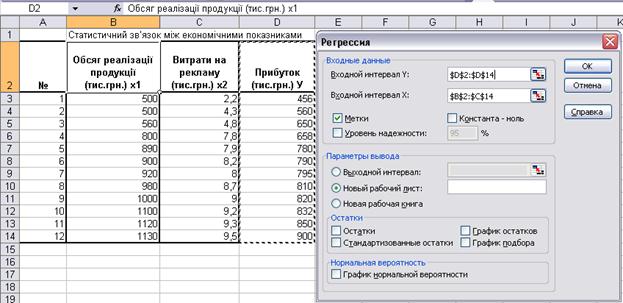
Рисунок 3.6 – Вікно діалогу «Регрессия»
У результаті виконання діалогу будуть отримані наступні дані (рис.3.7):

Рисунок 3.7 – Регресійна статистика
На підставі коефіцієнтів, отриманих у результаті регресійного аналізу, становимо рівняння регресії:
Y=306,45+0,21x1+34,09x2
Зробимо оцінку значимості регресійної моделі.
Множинний коефіцієнт детермінації R2 близький до одиниці та склав 0,962. Це означає, що лінія регресії точно відповідає всім спостереженням, і є достовірною.
Розглянемо технологію перевірки моделі на адекватність на основі F - критерію Фішера.
Fрасч = 56,79.
Табличне значення F - критерію при довірчій ймовірності 0,9 (тобто при a=0,05 і v1= 2-1=1; v2= 12-2=10 ) становить 4,96 (додаток А).
Розраховане значення 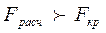 .
.
Це означає, що рівняння регресії є достовірним.
Зробимо оцінку значимості коефіцієнтів регресії за допомогою t-критерію Ст’юдента.
У результаті проведеного регресійного аналізу одержали наступні значення t-критерію Ст’юдента:
Обсяг реалізації продукції – 1,21,
Витрати на рекламу – 1,98.
По таблиці розподілу Ст’юдента знайдемо критичні значення t-критерію Ст’юдента. Табличне значення критерію при 95% рівні значимості та 9-ти ступенях волі (12-2-1=9) становить 0,129 (додаток Б).
В наслідок того, що для показника обсягів реалізації табличне значення критерію менше за розрахункове (0,129<1,21), то коефіцієнт а1 варто визнати значимим.
В наслідок того, що для показника витрат на рекламу табличне значення критерію менше за розрахункове (0,129<1,98), то коефіцієнт а2 варто визнати значимим.
Таким чином, побудована регресійна модель прибутку придатна і для аналізу, і для прогнозування.
Проведемо аналіз моделі. Аналіз коефіцієнтів множинної регресії Y=306,45+0,21x1+34,09x2 дозволяє зробити висновок про ступінь впливу кожного із двох факторів на показник прибутку.
Так наприклад, а1=0,21, це свідчить про те, що зі збільшенням обсягів реалізації продукції на 1 тис. грн. варто очікувати збільшення прибутку на 0,21 тис. грн. (прямий зв’язок).
а2=34,09, це означає, що підвищення витрат на рекламу на 1тис. грн. може привести до збільшення прибутку на 34,09 тис. грн. Звідси можна зробити відповідні практичні висновки та здійснити заходи, спрямовані на підвищення показника прибутку.
Але на основі коефіцієнтів регресії не можна сказати, який з факторних показників найбільш впливає на результативний показник, тому що коефіцієнти регресії між собою не порівнянні, оскільки вони обмірювані різними одиницями. На їхній основі не можна також установити в розвитку яких факторів закладені найбільш великі резерви зміни результативного показника, тому що в коефіцієнтах регресії не врахована варіація факторних показників. Відповіді на ці питання можна одержати, розрахувавши коефіцієнти еластичності.
Для цього в чарунки J18 і J19 необхідно ввести формулу для розрахунку коефіцієнта еластичності (3.7):
J18=B18*Лист4!B3/Лист4!F3,
J19=B19*Лист4!D3/Лист4!F3.
Та встановити відсотковий формат чарунок J18 і J19.
У результаті отримано наступні коефіцієнти еластичності для показників:
Обсяг реалізації продукції – 24,64%,
Витрати на рекламу – 34,05%.
Аналіз приватних коефіцієнтів еластичності показує, що за абсолютним приростом найбільший вплив на показник прибутку чинить показник витрат на рекламу, тобто підвищення витрат на рекламу на 1% приводить до зростання показника прибутку на 34,05%. Підвищення показника обсягів реалізації продукції на 1% підвищує показник прибутку на 24,64%.
3.5 Прогнозування значень економічних показників на основі регресійних моделей у Microsoft Excel
Побудовані регресійні моделі можна використовувати не тільки для аналізу економічних явищ і процесів, але і для прогнозування заснованих на екстраполяції заданих ознак. Застосування таких методів доцільно у випадках стійкої екстраполяційної спрямованості досліджуваного явища. Тобто, коли можна припустити, що діяльність у минулому мала певну тенденцію, яку можна очікувати в перспективі, наявній інформації досить для внесення можливих коректив і виявлення статистично достовірних залежностей.
Екстраполяція – прогнозування тенденції розвитку економічного показника на певний період упередження.
Період упередження – відрізок часу від моменту, для якого є останні статистичні дані про досліджуваний об’єкт, до моменту, до якого ставиться прогноз.
Період упередження варто планувати принаймні в 2 рази коротше, ніж період спостереження.
Екстраполяція дає можливість одержати крапкове значення прогнозу. Точний збіг фактичних даних і прогностичних крапкових оцінок, отриманих шляхом екстраполяції кривих, що характеризують тенденцію, має малу ймовірність. Виникнення таких відхилень пояснюється наступними причинами:
1. Обрана для прогнозування крива не є єдино можливою для опису тенденції. Можна підібрати таку криву, що дає більш точний результат.
2. Виконання прогнозу здійснюється на підставі обмеженого числа вихідних даних. Крім того, кожний вихідний рівень має ще випадковий компонент. Тому й крива, по якій здійснюється екстраполяція, буде містити випадковий компонент.
Будь-який статистичний прогноз носить наближений характер. Тому доцільно визначення довірчих інтервалів прогнозу. Величина довірчого інтервалу визначається в такий спосіб:
 , (3.8)
, (3.8)
де 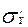 - середня квадратична помилка рівняння регресії;
- середня квадратична помилка рівняння регресії;
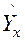 - значення результуючої ознаки, отримане по рівнянню регресії;
- значення результуючої ознаки, отримане по рівнянню регресії;
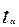 - визначається відповідно до рівня значимості по t – розподілу Ст’юдента.
- визначається відповідно до рівня значимості по t – розподілу Ст’юдента.
Період упередження повинен бути в три рази коротше періоду спостережень.
При прогнозі необхідно враховувати наступні опорні моменти.
1. До початку прогнозування необхідно визначити спрямованість прогнозу та його мету.
2. Варто представити перелік можливих рішень (управлінський рівень рішень), які можуть бути прийняті на основі прогнозу.
3. Для визначення обмежень необхідно обумовити необхідну точність прогнозу.
4. Деякі рішення небажано приймати навіть у тих випадках, коли ймовірність здійснення прогнозу 90-95 %, тому що занадто велика ціна помилки.
Однак є рішення, які можна приймати при значно менших ймовірностях здійснення прогнозу.
5. При оцінці вірогідності прогнозу необхідно визначити ті зміни, які можуть відбутися й вплинути на розвиток подій.
6. Після визначення джерел інформації встановлюються цінність минулого досвіду (ретроспективний аналіз), швидкість і обсяг поточних змін.
Побудуємо прогноз показника прибутку залежно від показників (змінні витрати на од. продукції, торговельна націнка на од. продукції).
По отриманому рівнянню регресії спрогнозуємо результуючий фактор на два періоди упередження, припускаючи обсяг реалізації продукції в першому періоді – 1500 тис. грн.., в другому – 1600 тис грн., витрати на рекламу в першому періоді – 10 тис. грн.., в другому – 10,5 тис грн. Прогнозне значення показника прибутку наведено в табл. 3.4.
Таблиця 3.4 – Прогнозне значення показника прибутку
| період прогнозу | Обсяг реалізації продукції (тис.грн.) х1 | Витрати на рекламу (тис.грн.) х2 | Прогноз прибутку | Нижня границя довірчого інтервалу | Верхня границя довірчого інтервалу |
| 963,65 | 958,53 | 968,76 | |||
| 10,5 | 1001,78 | 996,67 | 1006,89 |
Для побудови прогнозу та довірчих інтервалів необхідно ввести формули (3.8) як це показано на рис. 3.8.

Рисунок 3.8- Формульний вид прогнозу показника прибутку
3.6 Контрольні питання
1. Дайте визначення регресійного аналізу. Які показники використовуються для регресійного аналізу?
2. У яких випадках зв’язок між показниками є кореляційним?
3. Дайте інтерпретацію значень лінійного коефіцієнта кореляції?
4. Які існують види зв’язків між показниками?
5. Перелічить вимоги, пропоновані до показників у кореляційно-регресійному аналізі. Дайте визначення мультиколінеарності.
6. До яких проблем приводить наявність мультиколінеарності. Перелічить причини виникнення мультиколінеарності.
7. Проаналізуйте типи функцій, що використовуються для побудови регресійної моделі.
8. Які критерії апроксимації використовуються в кореляційно-регресійному аналізі для вибору типу функції процесу що моделюється?
9. За допомогою якого критерію можна оцінити вірогідність регресійної моделі?
10. Як оцінюється значимість коефіцієнтів регресії?
11. Дайте інтерпретацію коефіцієнтів регресії, кореляції, еластичності.
12. Дайте визначення періоду упередження й екстраполяції.
13. З яких причин точний збіг фактичних даних і прогностичних крапкових оцінок є мало ймовірним.
14. Які фактори необхідно враховувати при прогнозі?
15. За яким критерієм перевіряється придатність факторів для прогнозування?
3.7 Практичні завдання
У ході виконання практичного завдання необхідно виконати наступні дії:
1. Зробити відбір факторів при заданих значеннях параметрів.
2. Побудувати лінійну багатофакторну регресійну модель при заданих значеннях вхідних параметрів, перевірити її адекватність.
3. Зробити аналіз регресійної моделі по розрахованих коефіцієнтах регресії, кореляції, еластичності.
4. Зробити прогноз економічного показника по побудованій моделі, якщо модель придатна для прогнозування.
5. Роздрукувати результати виконання завдання.
Звіт про хід виконання практичного завдання повинен включати: титульний аркуш, роздруківку ходу виконання завдання, економічні висновки за результатами дослідження набрані в Word.
Варіант №1
| Валовий обсяг продажів (тис. грн) | x1 | |||||||
| Втрати та податки із продажів (тис. грн) | x2 | 6,5 | ||||||
| Сировина та матеріали (тис. грн) | x3 | |||||||
| Валовий прибуток (тис. грн) | Y |
Варіант №2
| Надходження від продажів (тис. грн.) | x1 | 26,7 | 35,6 | 17,5 | 35,8 | 13,0 | 37,8 | 35,1 |
| Надходження від оренди (тис. грн.) | x2 | 16,8 | 29,5 | 16,3 | 27,2 | 8,4 | 40,4 | 28,2 |
| Витрати на рекламу (тис. грн) | x3 | 0,8 | 4,4 | 3,3 | 2,6 | 5,9 | 2,6 | 1,4 |
| Прибуток підприємства (тис. грн.) | Y | 33,8 | 24,4 | 35,6 | 43,4 | 19,1 | 19,1 | 23,4 |
Варіант №3
| Операційні витрати (тис. грн.) | x1 | 0,4 | 2,1 | 5,0 | 4,7 | 4,9 | 1,5 | 6,0 | 3,7 |
| Торговельні витрати (тис. грн.) | x2 | 8,4 | 12,4 | 14,0 | 14,2 | 16,2 | 16,3 | 16,8 | 17,0 |
| Адміністративні витрати (тис. грн.) | x3 | 2,4 | 3,2 | 4,5 | 4,7 | 7,7 | 3,3 | 6,8 | 5,0 |
| Сумарні витрати (тис. грн.) | Y |
Варіант №4
| Транспортні витрати (тис. грн.) | x1 | 3,5 | 2,9 | 1,4 | 2,1 | 2,6 | ||||
| Витрати на рекламу (тис. грн.) | x2 | 3,1 | 1,9 | 4,5 | 1,3 | 2,3 | 2,0 | 1,8 | 1,1 | 1,3 |
| Виторг (тис. грн.) | x3 | |||||||||
| Прибуток (тис. грн.) | Y |
Варіант №5
| Обсяг реалізації продукції через INTERNET, тис грн. | x1 | |||||||
| Витрати на рекламу в INTERNET, тис грн. | x2 | |||||||
| З/п торговельного агента (тис. грн.) | x3 | 6,4 | 3,7 | 3,4 | 7,6 | 3,6 | 3,5 | 6,5 |
| Виторг (тис. грн.) | Y |
Варіант №6
| Змінні витрати (тис. грн.) | x1 | ||||||||
| Податок на прибуток (тис. грн.) | x2 | ||||||||
| Виторг від реалізації (тис. грн.) | x3 | ||||||||
| Чистий прибуток (тис. грн.) | Y |
Варіант №7
| Торгова площа (м2) | x1 | |||||||||
| Витрати на рекламу (тис. грн.) | x2 | 5,4 | 7,4 | 7,8 | 8,5 | 9,5 | 2,0 | 7,0 | 6,4 | 8,7 |
| Запаси (тис. грн) | x3 | 76,8 | 79,2 | 90,4 | ||||||
| Валовий доход (тис. грн.) | Y |
Варіант №8
| Інвестиції (тис. грн.) | x1 | |||||||
| Дивіденди (тис. грн.) | x2 | |||||||
| Товарні запаси (тис. грн.) | x3 | |||||||
| Оборотний капітал (тис. грн.) | Y |
Варіант №9
| Наявні кошти (тис. грн.) | x1 | |||||||
| Інвестиції (тис. грн.) | x2 | |||||||
| Довгострокова заборгованість (тис. грн.) | x3 | |||||||
| Прибуток (тис. грн.) | Y |
Варіант №10
| Виторг від реалізації продукції (тис. грн.) | x1 | ||||||||
| Витрати на збут (тис. грн.) | x2 | 2,2 | 3,9 | 1,8 | 1,9 | ||||
| Відсотки за капітал (%) | x3 | ||||||||
| Загальний дохід до сплати податків (тис. грн.) | Y |
Варіант №11
| Валовий обсяг продажів (тис. грн.) | x1 | |||||||||
| Запаси (тис. грн.) | x2 | |||||||||
| Інвестиції (тис. грн.) | x3 | |||||||||
| Прибуток (тис. грн.) | Y |
Варіант №12
| Постійні витрати (тис. грн.) | x1 | 6,1 | 6,6 | 7,3 | 8,1 | 8,7 | 9,5 | 10,4 |
| Змінні витрати (тис. грн.) | x2 | 11,2 | 11,7 | 12,4 | 13,7 | 14,4 | 15,9 | 17,1 |
| Валовий обсяг продажів (тис. грн.) | x3 | |||||||
| Рентабельність діяльності підприємства (%) | Y | 17,8 | 17,6 | 17,4 |
Варіант №13
| Операційні витрати (тис. грн.) | x1 | |||||||
| Торговельні витрати (тис. грн.) | x2 | |||||||
| Адміністративні витрати (тис. грн.) | x3 | |||||||
| Сумарні постійні витрати (тис. грн.) | Y |
Варіант №14
| Торгова площа (м2) | x1 | 14,9 | 14,2 | 18,5 | 17,5 | 10,9 | 15,4 | |
| Товарні запаси (тис. грн.) | x2 | 17,6 | 15,4 | 15,6 | 13,2 | 12,1 | ||
| Знижка (%) | x3 | 0,7 | ||||||
| Товарообіг (тис. грн.) | Y |
Варіант №15
| Валовий обсяг продажів (тис. грн.) | x1 | |||||||
| Товарні запаси (тис. грн.) | x2 | |||||||
| Інвестиції (тис. грн.) | x3 | |||||||
| Валовий доход (тис. грн.) | Y | 4,3 | 4,9 | 5,6 | 6,4 | 6,8 | 7,4 | 9,8 |
| Питання | Варіанти відповідей | |||||||
| 1. Укажіть відповідність між значенням коефіцієнта кореляції й характером зв’язку. | a. r=0, b. r=(1(, c. r є (-1;0), d. r є (0,3;0,5). | 1. Слабкий. 2. Зворотний. 3. Відсутній. 4. Функціональний. | ||||||
| 2. Укажіть відповідність між записом функції й найменуванням. | a.  ,
b. ,
b. 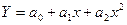 ,
c. ,
c.  ,
d. ,
d.  , ,
| 1. Парабола 2. Показова 3. Ступенева 4. Гіпербола | ||||||
| 3. За допомогою критерію Фішера перевіряється: |
| |||||||
| 4. Пряма регресія має місце коли: |
| |||||||
| 5.Для кількісної оцінки тісноти зв'язку між показниками використовується: |
| |||||||
| 6. Яка функція обирається для побудови регресійної моделі при зворотному зв'язку між аналізованими показниками: | a.  ,
b. ,
b. 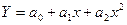 ,
c. ,
c.  ,
d. ,
d.  , ,
| |||||||
| 7. Для визначення частки впливу фактору на результативний показник використовується коефіцієнт: | a. Детермінації. b. Регресії. c. Кореляції. d. Еластичності. | |||||||
| 8. Яку функцію необхідно вибрати для економічного аналізу, при відомих значеннях показника середньої квадратичної помилки. | a. Гіперболічна - 33%. b. Статечна – 11,8. c. Показова - 4,56. d. Лінійна - 19%. | |||||||
| 9. Якщо модель за критерієм Фішера адекватна і її коефіцієнти не значимі, то: | a. Модель може бути використана для прийняття рішень і прогнозування. b. Модель може використовуватися тільки для аналізу. c. Модель не може бути використана для прийняття рішень. | |||||||
| 10. Число факторів, що включаються в модель повинно бути: | a. В 2 рази менше обсягу досліджуваної сукупності. b. В 5 разів менше обсягу досліджуваної сукупності. c. В 3 рази менше обсягу досліджуваної сукупності. d. Відповідати обсягу досліджуваної сукупності. | |||||||
Змістовний модуль 2 Автоматизація ведення господарських операцій у середовищі 1С:Підприємство 7.7
4 Інформаційні технології ведення господарських операцій у середовищі програми "1С: Підприємство 7.7"
4.1 Користувальницький інтерфейс програми "1С:Підприємство 7.7"
Система “ 1С:Підприємство 7.7” є універсальною програмою автоматизації організаційної, економічної й фінансової діяльності підприємства. В наслідок того, що така діяльність може бути досить різноманітною, система «1С:Підприємство 7.7» має можливість адаптуватися до особливостей конкретної області діяльності, у якій вона використовується.
Використання в навчальному процесі програмного продукту «1С: Підприємство 7.7» при підготовці майбутніх фахівців в області управління підприємством дасть можливість студентам одержати практичні навички оцінки аналізу й контролю операцій, пов'язаних з веденням торговельно-економічної діяльності підприємства, складання звітних фінансових документів таких, як форма №1 «Баланс», форма №2 «Звіт про фінансові результати», форма №3 «Звіт про рух грошових коштів».
Програма “ 1С:Підприємство 7.7” працює в операційній системі Windows. Найпростіший спосіб запуску програми є меню Пуск.
При встановленні програми “1С:Підприємство 7.7” на комп'ютер у меню Пуск у групі Програми автоматично створюється нове підменю (група) 1С:Підприємство. У цю групу входить програма запуску компонент системи, що також має назву “ 1С:Підприємство”.
Процес запуску програми “1С:Підприємство” в операційних системах Windows показаний на рис. 4.1. Він передбачає виконання наступної послідовності дій:
1) курсором миші натиснути екранну кнопку Пуск;
2) у меню, що відкрилося, вибрати пункт Програми;
3) у відповідному підменю вибрати пункт 1С:Підприємство;
4) у переліку режимів запуску вибрати модуль запуску системи: 1С:Підприємство або 1С:Монопольно.

Рисунок 4.1 - Запуск програми “1С:Підприємство”
Режим “1С:Монопольно” призначений для запуску сітьової версії програми у монопольному (однокористувальницькому) режимі. Після виконання зазначеної послідовності дій на екрані з'явиться вікно запуску режимів системи “1С:Підприємство”, що зображено на рис. 4.2

Рисунок 4.2 - Вікно запуску режимів програми “1С:Підприємство 7.7”
Вікно містить такі поля і елементи керування:
В режиме – у даному полі виконується вибір одного з можливих режимів роботи користувача із системою: “1С:Підприємство”, “Конфігуратор”, “Отладчик”. Для вибору необхідного режиму роботи варто натиснути мишею на даному полі і у списку, який з'явився, вибрати бажаний режим.
Поле Информационные базы містить список інформаційних баз, доступних для роботи. Повний путь до папки з обраною інформаційною базою вказується у нижній частині вікна.
Поле Монопольно міститься у вікні запуску тільки при використанні сітьової версії системи “1С:Підприємство”. Це поле використовується для встановлення монопольного режиму роботи із програмою, тобто такого режиму, якщо обрана для роботи база даних стає недоступною для інших користувачів мережі. Натискання мишею на даному полі приведе до появи або зникнення позначки (прапорця) у вигляді “галочки”. Наявність позначки свідчить про те, що встановлено монопольний режим роботи.
При першому запуску програми варто спочатку запустити режим “Конфігуратор”. Після того, як базові налаштування конфігурації будуть збережені на диску, мож
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 622; Нарушение авторских прав?; Мы поможем в написании вашей работы!