Диаграмма состояния. Тройная точка

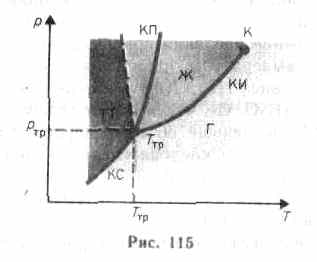Если система является однокомпонентной, т. е. состоящей из химически однородного вещества или его соединения, то понятие фазы совпадает с понятием агрегатного состояния. Одно и то же вещество в зависимости от соотношения между удвоенной средней энергией, при­ходящейся на одну степень свободы ха­отического теплового движения молекул, и наименьшей потенциальной энер­гией взаимодействия молекул может на­ходиться в одном из трех агрегатных состояний: твердом, жидком или газооб­разном. Это соотношение, в свою очередь, определяется внешними условиями - тем­пературой и давлением. Следовательно, фазовые превращения также определяют­ся изменениями температуры и давления. Для наглядного изображения фазовых превращений используется диаграмма со­стояния (рис. 115), на которой в коорди­натах задается зависимость между температурой фазового перехода и давле­нием в виде кривых испарения (КИ), плавления (КП) и сублимации (КС), раз­деляющих поле диаграммы на три об­ласти, соответствующие условиям су­ществования твердой (ТТ), жидкой (Ж) и газообразной (Г) фаз. Кривые на ди­аграмме называются кривыми фазового равновесия, каждая точка на них соответствует условиям равновесия двух сосуще­ствующих фаз: КП — твердого тела и жидкости, КИ — жидкости и газа, КС — твердого тела и газа.

Точка, в которой пересекаются эти кривые и которая, следовательно, опреде­ляет условия (температуру 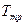и соответ­ствующее ей равновесное давление ) одновременного равновесного сосущество­вания трех фаз вещества, называется тройной точкой. Каждое вещество имеет только одну тройную точку. Тройная точка воды характеризуется температурой 273,16 К (по шкале Цельсия ей соответ­ствует температура 0,01 °С) и является ос­новной реперной точкой для построения термодинамической температурной шкалы.

Термодинамика дает метод расчета кривой равновесия двух фаз одного и того же вещества. Согласно уравнению Кла­пейрона — Клаузиуса, производная от равновесного давления по температуре

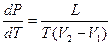(11.1)

где 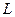— теплота фазового перехода, 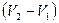— изменение объема вещества при переходе его из первой фазы во вто­рую, 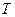— температура перехода (процесс изотермический).

Уравнение Клапейрона — Клаузиуса позволяет определить наклоны кривых равновесия. Поскольку 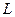и 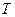положитель­ны, наклон задается знаком 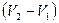. При испарении жидкостей и сублимации твер­дых тел объем вещества всегда возраста­ет, поэтому, согласно (11.1), 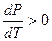; следовательно, в этих процессах повыше­ние температуры приводит к увеличению давления, и наоборот. При плавлении большинства веществ объем, как правило, возрастает, т. е. 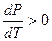; следовательно, увеличение давления приводит к повыше­нию температуры плавления (сплошная КП на рис. 115). Для некоторых же ве­ществ (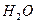, , чугун и др.) объем жид­кой фазы меньше объема твердой фазы, т. е. 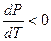; следовательно, увеличение давления сопровождается понижением температуры плавления (штриховая ли­ния на рис. 115).

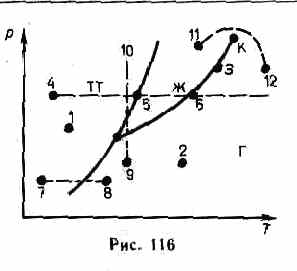Диаграмма состояния, строящаяся на основе экспериментальных данных, позво­ляет судить, в каком состоянии находится данное вещество при определенных и , а также какие фазовые переходы будут происходить при том или ином процессе. Например, при условиях, соответствую­щих точке 1 (рис. 116), вещество находит­ся в твердом состоянии, точке 2 — в газо­образном, а точке 3 — одновременно в жидком и газообразном состояниях. До­пустим, что вещество в твердом состоянии, соответствующем точке 4, подвергается изобарному нагреванию, изображенному на диаграмме состояния горизонтальной штриховой прямой 4—5—6. Из рисунка видно, что при температуре, соответствую­щей точке 5, вещество плавится, при более высокой температуре, соответствующей точке 6 — начинает превращаться в газ. Если же вещество находится в твердом состоянии, соответствующем точке 7, то при изобарном нагревании (штриховая прямая 7—8) кристалл превращается в газ минуя жидкую фазу. Если вещество находится в состоянии, соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9—10) оно пройдет следующие три состояния: газ — жид­кость — кристаллическое состояние.

На диаграмме состояний (см. рис. 115 и 116) видно, что кривая испарения заканчивается в критической точке К. По­этому возможен непрерывный переход ве­щества из жидкого состояния в газообраз­ное и обратно в обход критической точки, без пересечения кривой испарения (пере­ход 11—12 на рис. 116), т. е. такой пере­ход, который не сопровождается фазовы­ми превращениями. Это возможно благо­даря тому, что различие между газом и жидкостью является чисто количественным (оба эти состояния, например, явля­ются изотропными). Переход же кристал­лического состояния (характеризуется анизотропией) в жидкое или газообразное может быть только скачкообразным (в ре­зультате фазового перехода), поэтому кривые плавления и сублимации не могут обрываться, как это имеет место для кри­вой испарения в критической точке. Кри­вая плавления уходит в бесконечность, а кривая сублимации идет в точку, где и .

Дата добавления: 2014-01-05