Determinants and their behaviours. Algebraic complements

Course of treatment

LINEAR ALGEBRA

Оглавление

1. Determinants and their behaviours. Algebraic complements. 3

Determinants of second order and their behaviours

In action researcher has to do with unknown values connected together by definite dependences, which can be determined by way of the different formulations.

For that the conditions row may be determined:

1. Formula’s coefficients should be constant.

2. Unknown parameters have only first degree.

3. There are not product between unknown parameters.

That dependences are known linear.

Example. 10 items have total weight 280 g. It is necessary to find the medium weight of one item, if the package weights 15 g.

Solution. Use simple equation:

10 x+15=280. 280 – 15 = 10 x = 280 -15. x =265/10 = 26.5.

We denote x - medium weight of one item. At that time equation solution is 26.5 g.

We have at that example the linear equation.

Then consider the following equations system:

10x + 10y = 280;

5x + 2y = 128,

and substitute coefficients by letters. We will have the linear equations system:

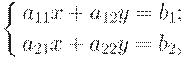
(1.1)

Here a₁₁, a₁₂, a₂₁, a₂₂, b₁, b₂ – some numbers, x, y - unknown parameters. Use that for the rectangular table with the next view:

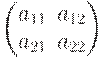
(1.2)

Determination. Matrix is anyrectangular table, containing the numbers _.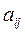

Determination. Items 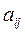are named elements of that matrix.

Determination. Determinant of the second order corresponding matrix (1.2) is that number D, if that equality is truth:

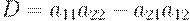
(1.3)

Determinant denotes by letters D or and can be written down:

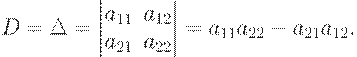
Example. Use simple equations system:

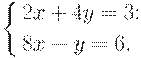
make up system’s matrix and calculate determinant.

Solution. We can to form the matrix:

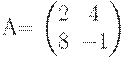
and we can to calculate the determinant

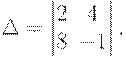
Use the formula (1.2), we will have

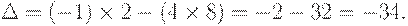
Determination. The number of lines or columns of the determinant is its order.

There is the second order of determinant at the last example.

Determinant has the following behavior:

1. Determinant das not change, if its lines are changed by columns or conversely.

Show it. We have the determinant:

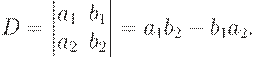
Change lines by columns and calculate new determinant. We will have:

Compare D with D^*. We can see, hat D = D^*.

Determination. The operation changing lines by columns or conversely into determinant is named a transposition.

2. If two lines or two columns are transposed that the determinant changes its sign.

Check it. We have following determinant:

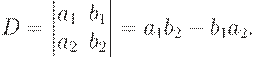
Change lines by columns and calculate new determinant. We will have:

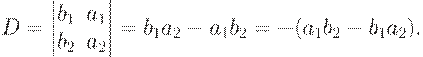
Than change columns by lines and calculate new determinant. We will have:

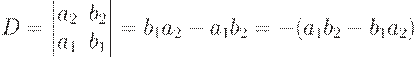
You can check each property.

3. If all elements of some column (or line) are product (or divide) on same number m does not equal zero, that determinant is product (divide) on this number m:

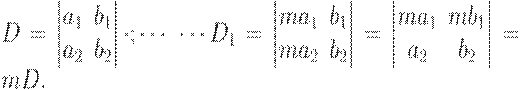
4. Determinant, which has line’s elements (or column’s elements) proportional to elements other one, is equal zero.

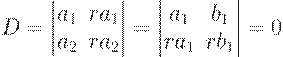
5. If each element of any line (column) can be realized as the sum of two items, that the determinant will be equal the sum of two determinants.

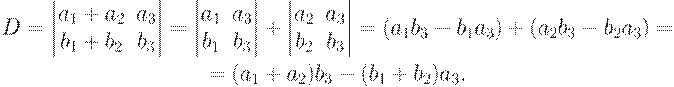
We can see that property is true by compare this result.

This property is used widely for practical calculations when determinant

has the order more than 3.

6. Determinant das not change, if we add to elements of each column (line) corresponding elements of other multiplied before on some number:

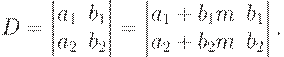
Determinant is very convenient mathematic form, which allows to find quickly the solution of linear equations system.

Determinants of third order and their properties

In practice we have systems with more than two equations. And we have many unknown variables.

Consider the following system:

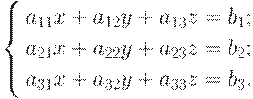
(1.4)

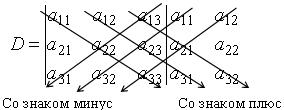
Determination. Determinant of the third order corresponding to the matrix (1.4) symbolized as D is the number, equals

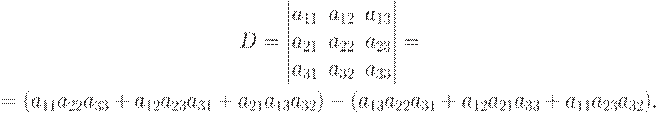
There are two schemes to solve determinant of the third order:

1. Rule of a triangle (rule of a star).

2. Sarrjus’s rule.

If we use first one, that it is necessary to multiply and sum elements on connected by lines of the scheme.

We have: a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂.

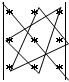
Than we have to multiply and sum elements on connected by lines of that scheme.

We have: a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂.

Than we calculate the determinant:

D = (a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂) - (a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂).

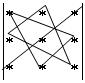
If we use Sarrjus’s rule, we should to add to the matrix right two first columns. And than we have to calculate the sum of multiplies determinant’s elements using one direction and than we have to subtract the sum of multiplies determinant’s elements other direction (look the scheme):

The results of both methods are equal.

All second order determinant properties are right for the third order determinant.

Using that we will formulate common properties of the any order determinant:

· Determinant value das not change if we change lines by columns or by the other way.

· Transposition of two lines or two columns between each other gives a sign change of the determinant.

· Determinant, which has two equivalent (proportional) lines (columns) equals to zero.

· If all elements of some line (column) contain the same multiplier, that this multiplier may be carry out sign of the determinant.

· Determinant equals zero when all elements of some line (column) equal zero.

· Determinant value das not change, if we add to some line (columns) elements corresponding elements of the other line (column) multiplied theirs on the same multiplier.

Дата добавления: 2014-01-05