Тени от геометрических тел

Как уже говорилось выше, падающая тень от геометрического образа является тенью от линии, являющейся контуром его собственной тени. Поэтому в общем случае вначале определяется контур собственной тени геометрического образа, а затем контур падающей. Далее рассматривается построение теней от простейших геометрических тел: параллелепипеда, цилиндра, конуса, шара (сферы).

Тень от параллелепипеда. Контур собственной тени параллелепипеда ограничен прямыми линиями и поэтому построение теней от него не нуждается в комментариях (рис.4.1, 4.2). Необходимо лишь отметить, что если грани его параллельны плоскостям проекций, то ширина тени составляет величину a+b, т.е. сумму длин сторон основания.

Тень от цилиндра. Контур собственной тени вертикального цилиндра образован полуокружностью верхнего основания, полуокружностью нижнего основания и двумя образующими, которых касаются световые лучи (рис.4.3). Поэтому для построения падающей тени необходимо построить в общем случае тени от верхней и нижней окружностей и двух образующих. На рис.4.4, 4.5, 4.6 показано построение теней для различных положений цилиндра в пространстве, а также половины цилиндра, примыкающего к фронтальной плоскости.

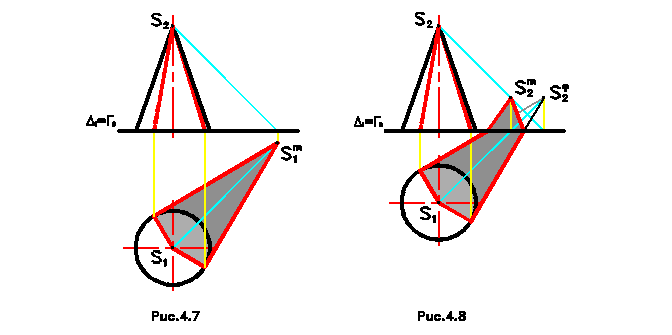
Тень от конуса. В отличие от других геометрических тел для конуса вначале строится падающая тень и лишь потом собственная. Для этого строится падающая тень от вершины конуса (рис.4.7). Из полученной точки S₁^т проводятся касательные прямые к основанию конуса. Контур, образованный этими касательными, и часть контура основания являются контуром падающей тени конуса. Образующие конуса, проведенные из точек касания, являются контуром собственной тени конуса. Если тень от вершины конуса падает на фронтальную плоскость, то строится, так называемая, фиктивная тень от вершины на горизонтальную плоскость, проводятся касательные к основанию конуса из этой точки, но только в пределах горизонтальной плоскости. Точки на линии пересечения плоскостей соединяются с истинной тенью от вершины (рис.4.8).

В случае если конус обратный, для построения собственной тени строится фиктивная тень от вершины на плоскость, в которой находится основание конуса (рис.4.9) и из нее проводятся касательные к основанию конуса.

На рис.4.10 представлена половина конуса, примыкающего к фронтальной плоскости и отстоящего от горизонтальной плоскости. Контур падающей тени такого конуса образован контуром падающей тени окружности основания и прямой, исходящей из вершины, (т.к. вершина конуса лежит во фронтальной плоскости) и касательной к тени от окружности. Если из точки касания провести обратный луч до основания, то из полученной точки 1 можно провести образующую, являющуюся контуром собственной тени.

На рис.4.11 и 4.12 представлены два конуса, у которых углы при основании равны 45⁰ и 35⁰ соответственно. Контур собственной тени для конуса с углом 45⁰ при основании образуют профильная и контурная образующие. Контур собственной тени для конуса с углом 35⁰ при основании вырождается в прямую, являющуюся образующей, совпадающей со световым лучом. Конусы с углами, меньшими 35⁰, не имеют собственной тени. Боковая поверхность таких конусов полностью освещена и не дает падающей тени.

На рис.4.13 показано графическое построение угла 35⁰ .Для этого строится квадрат, размер диагонали 1 – 2 циркулем переносится на сторону квадрата, полученная точка 3 соединяется с точкой 4. Угол между отрезками 1 – 3 и 3 – 4 составляет 35⁰.

Конусы с углами при основании 45⁰ и 35⁰ в дальнейшем будут использоваться при построении теней более сложных форм, т.к. положение их собственных теней заведомо известно и легко строится.

Тень от сферы. Собственная тень сферы является эллипсом, большая ось которого равна диаметру сферы d, а малая ось приблизительно равна 0,6d (рис.4.14).

Дополнительные точки на контуре собственной тени можно построить проведением вертикальных и горизонтальных прямых из концов большой оси до пересечения с вертикальной и горизонтальной осями сферы. Смысл построений станет ясен при изучении способов построения теней. Падающая тень от сферы является эллипсом, для построения которого строится тень от центра сферы. Перпендикулярно направлению проекции светового луча расположена малая ось этого эллипса, равная по величине диаметру сферы. Величина большой оси определяется засечкой, равной диаметру сферы, из концов малой оси на направление большой и равна 1,7d. На рис.4.15 построена тень от полусферы на фронтальную плоскость проекций.

Дата добавления: 2014-01-05