Принцип наложения и метод наложения

Чтобы составить общее выражение для тока в R-ветви сложной схемы, составим уравнение по методу контурных токов, выбрав контуры так, чтобы R-ветвь входила только в один R- контур (это всегда возможно).

Тогда ток в R-ветви будет равен контурному току I_kk по уравнению (*). Каждое слагаемое правой части (*) представляет собой ток, вызванный в R-ветви соответствующей контурной ЭДС, E_a. - составляющая тока R-ветви, вызванная контурной ЭДС E₁₁. Каждую из контурных ЭДС можно выразить через ЭДС ветвей E₁,E₂,E₃,…,E_k,….,E_n, сгруппировав коэффициенты при этих ЭДС, получим:

I=E₁g_k1+E₂g_k2+E₃g_k3+…+E_kg_kk+…+E_ng_kn (**)

Если контур выбран таким образом, что какая либо из ЭДС, E_a, E_m входит только в один m-контур, то g_km=Δ_km/Δ.

Уравнение (**) выражает собой принцип наложения.

Принцип наложения состоит в следующем:

ток в R-ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Этот принцип справедлив для всех линейных ЭЦ.

При расчете цепей по методу наложения поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные из схемы, но оставляя в схеме внутреннее сопротивление источников, и затем находят токи в ветвях путем алгебраического сложения частных токов.

Причем, метод наложения нельзя использовать для подсчета выделенных в сопротивлениях мощностей, как суммы мощностей от частичных токов, поскольку мощность является квадратичной функцией тока:

P=I²R.

Так, если через некоторое сопротивление R протекают токи I₁, I₂ (в одном направлении) то P=R(I₁+I₂)² и эта мощность не равна частичным мощностям:

Рассмотрим пример метода наложения и расчета баланса мощностей используя схему рисунка12:

R₁=2 Ом; R₂=4 Ом; R₃=: Ом; I_k=5 А; E=20 В.

Используя метод наложения найти токи в ветвях, рассчитать баланс мощностей.

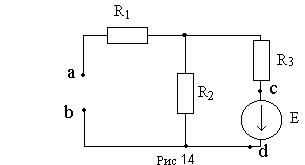
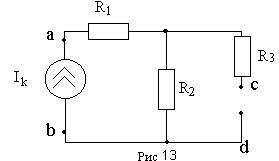
I₁^I=I_k; I₂^I=I₁^IR₂/(R₂+R₃); I₃^I=2A

I₁^II=0; I₂^II=-I₃^II=-E/(R₂+R₃)=-2A

I₁=I₁^I+I₁^II=5+0=5 A; I₂=I₂^I+I₂^II=3-2=1 A; I₃=I₃^I+I₃^II=2+2=4 A

U_ab=I₁R₁+I₂R₂=1*4+5*2=14 B

Баланс мощностей: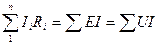

I₁²R₁+I₂²R₂+I₃²R₃=U_ab+EI₃;

25*2+1*4+16*6=14*5+20*4;

150=150

Дата добавления: 2014-01-05