Взаимно однозначное соответствие. Мощность множества. Счетные, несчетные, континуальные множества и их свойства

Иногда бывает необходимо сопоставлять друг с другом элементы некоторых множеств. Рассмотрим, например, два множества: стадо из четырехсот овец и рощу из четырехсот деревьев. Эти множества можно попарно сопоставить друг с другом, привязав овец к деревьям, так что каждая овца и каждое дерево будут в точности принадлежать одной определенной паре. Ни одно из данных множеств не может быть по такому принципу попарно сопоставлено, например, с рощей из семисот деревьев или с множеством из трехсот камней.

Для взаимно однозначного соответствия можно дать следующее определение.

Определение 2.2.1. Взаимно однозначным соответствием между двумя непустыми множествами А и В называется такое правило (или закон) f, по которому каждому элементу а Î А ставится в соответствие единственный элемент f (а) Î В и для любого элемента b Î В существует единственный элемент а Î А, такой что f (а) = b, другими словами, f задает биекцию между А и В.

Определение 2.2.2. Множества А и В называются равномощными (обозначение А «В), если между ними можно установить взаимно однозначное соответствие.

Очевидно, что если множество А равномощно В, а В равномощно С, то А равномощно С, то есть А «В & В «С Þ А «С – свойство транзитивности.

Определение 2.2.3. Число элементов в конечном множестве А называется мощностью А и часто обозначается | А |. Пустое множество, то есть не содержащее элементов, относят к конечным, оно является множеством мощности 0: | Æ | = 0.

Мощность бесконечного множества – более сложное понятие. Оно будет рассмотрено ниже.

Теорема 2.2.1. Между непустыми конечными множествами А и В существует взаимно однозначное соответствие тогда и только тогда, когда | А | = | В |.

Необходимость. Пусть f: А ® В задает взаимно однозначное соответствие между множествами. Пусть | А | ¹ | В |, допустим, | А | < | В |. Тогда, поскольку для любого a Î A существует единственный элемент b Î B такой, что f (a) = b, для некоторого с Î В не найдется элементов из А с таким свойством, а это противоречит определению взаимно однозначного соответствия (сюръективности). Предположим теперь, что | В | < | А |. Тогда, поскольку f определено всюду на А, $ a ₁, a ₂ Î A такие, что f (a ₁) = f (a ₂) = b Î B. Снова получаем противоречие с тем, что f задает взаимно однозначное соответствие (противоречие инъективности). Итак, | А | = | В |.

Достаточность. Пусть | А | = | В | = n Î N. Тогда А = { а ₁, а ₂,…, а_n }, В = { b ₁, b ₂,…, b_n }. Рассмотрим правило f, по которому каждому элементу а_i Î А ставится в соответствие единственный элемент b_i Î B. Тогда для " b_i Î B существует единственный элемент a_i Î A, такой что f (a_i) = b_i. Значит, f задает взаимно однозначное соответствие между множествами А и В.

В связи с этой теоремой становится понятно, почему два первых множества из примера в начале параграфа находятся во взаимно однозначном соответствии друг с другом, но не являются равномощными третьему и четвертому множествам. Сколько же существует таких взаимно однозначных соответствий для двух n -элементных множеств А и В?

Теорема 2.2.2. Общее число взаимно однозначных соответствий для двух n -элементных множеств равно n!.

Первый элемент множества А может быть сопоставлен с любым из n элементов множества В. Для каждого такого сопоставления второй элемент множества А может быть сопоставлен с любым из оставшихся n – 1 элементов множества В и т.д. После того, как такое сопоставление проведено для n – 1 элементов множества А, последний элемент этого множества будет сопоставляться с единственным оставшимся элементом множества В. Таким образом, общее число взаимно однозначных соответствий для n -элементных множеств будет равно

n × (n – 1) × (n – 2) ×…× 2 × 1 = n!.

Теорема 2.2.3. Пусть А ₁,…, А_n – конечные множества и | A_i | = m_i, 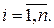Тогда мощность множества А ₁ ´ А ₂ ´…´ А_n = {(a ₁, a ₂,…, a_n) | a_i Î A_i, 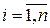} равна произведению мощностей множеств А ₁, А ₂,…, А_n:

| A ₁ ´ A ₂ ´…´ A_n | = m ₁ × m ₂ ×…× m_n.

Эту теорему докажем методом математической индукции. Для n = 1 теорема тривиально верна. Предположим, что она верна для n = k, и докажем ее справедливость для n = k + 1. По индуктивному предположению | A ₁ ´ A ₂ ´…´ A_k | = m ₁ × m ₂ ×…× m_k. Возьмем любой вектор (a ₁, a ₂,…, a_k) из А ₁ ´ А ₂ ´…´ А_k и припишем справа элемент a_{k + 1} Î А_{k + 1}. Таким образом, из всех m ₁ × m ₂ ×…× m_k векторов из А ₁ ´ А ₂ ´…´ А_k приписыванием справа элемента из А_{k + 1} можно получить m ₁ ×…× m_k × m_{k + 1} векторов из А ₁ ´ А ₂ ´…´ А_k ´ А_{k + 1}, причем все они различны и никаких других векторов в А ₁ ´ А ₂ ´…´ А_{k + 1} не содержится. Поэтому и для n = k + 1 теорема верна и, следовательно, верна для любых n Î N.

Если A_i = А, 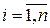, то 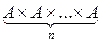= Аⁿ = {(a ₁, a ₂,…, a_n) | a_i Î A, }.

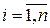Следствие. | Aⁿ | = | A | ⁿ для любого n Î N.

Теорема 2.2.3 и следствие из нее лежат в основе очень многих комбинаторных фактов.

Определение 2.2.4. Пусть А – некоторое множество. Множеством-степенью или булеаном множества А называется множество Р (А) = { Х | Х Í A } – множество всех подмножеств множества А.

Вернемся к теореме 2.2.1. Во-первых, она позволяет установить равенство мощностей двух конечных множеств, не вычисляя этих мощностей, а во-вторых, часто дает возможность вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется. В качестве иллюстрации этого приема докажем важную теорему о числе подмножеств конечного множества.

Теорема 2.2.4. Для любого конечного множества А, | A | = n Î Z _³0, число всех подмножеств А равно 2 ⁿ, то есть | P (A) | = 2 ⁿ.

| Æ | = 0. Очевидно, что Р (Æ) = {Æ} и | Р (Æ) | = 1 = 2⁰.

Пусть n Î N. Рассмотрим множество В_n всех двоичных слов (векторов) из нулей и единиц длиной n. Каждому подмножеству В Í А сопоставим двоичное слово S_B длиной n, построенное по следующему правилу:

S_B = (a ₁,…, a_n), где a_i =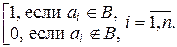

Таким образом, каждому подмножеству множества А ставится в соответствие единственное двоичное слово длиной n и каждому двоичному слову длиной n ставится в соответствие единственное подмножество множества А. Данное сопоставление задает взаимно однозначное соответствие между булеаном множества А Р (А) и множеством В_n. Согласно теореме 2.2.1 | Р (А) | = | В_n |. А так как В_n является n -ой декартовой степенью двухэлементного множества {0, 1}, то в силу следствия из теоремы 2.2.3 | В_n | = 2 ⁿ. Итак, | Р (А) | = 2 ⁿ.

Пусть требуется определить число всех k -элементных подмножеств n -элементного множества А, n Î Z _³0. Очевидно, что k должно удовлетворять неравенству: 0 £ k £ n. Если А = Æ, то n = k = 0 и число 0-элементных подмножеств равно | P (Æ) | = 1. Пусть теперь n Î N. Поскольку, как уже было сказано в доказательстве теоремы 2.2.4, множества Р (А) и В_n равномощны, то число всех k -элементных подмножеств в А равно числу всех двоичных слов длиной n, в которых k символов равны 1, а остальные равны 0. Это число равно числу сочетаний из n элементов по k: 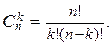Когда n = k = 0, мы получаем 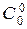= 1, то есть частный случай этой формулы. Этот факт также является иллюстрацией применения теоремы 2.2.1.

Если множества являются бесконечными, то установление между ними взаимно однозначного соответствия наталкивается на трудности, связанные с необходимостью оперировать с бесконечно большим числом элементов множества. За основу для сопоставления бесконечных множеств принято брать натуральный ряд чисел N: 1, 2, 3,…, n,…

Определение 2.2.5. Множество, равномощное множеству натуральных чисел N, называется счетным.

Вообще любое бесконечное подмножество множества N счетно. Действительно, пусть 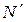Ì N. Выберем в 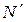наименьший элемент и обозначим его n ₁; в 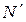\{ n ₁} выберем наименьший элемент и обозначим его n ₂; наименьший элемент в 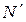\{ n ₁, n ₂} обозначим n ₃ и т.д. Для всякого натурального числа n имеется лишь конечное множество меньших натуральных чисел: Æ, если n = 1, и {1, 2,…, n – 1}, если 1 < n. Таким образом, любой элемент 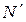рано или поздно получит свой номер. Эта нумерация, то есть функция f: 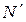® N, f (n_i) = i, и есть взаимно однозначное соответствие между 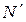и N.

Счетным является множество всех целых чисел Z, хотя N Ì Z. Это можно установить, рассмотрев взаимно однозначное соответствие f: Z ® N, представленное на рис. 2.2.1.

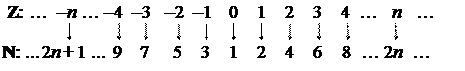Рис. 2.2.1

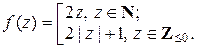
Еще более удивителен тот факт, что счетным является множество всех рациональных чисел Q. Докажем сначала счетность множества Q _>0. Q _>0 = { m / n | m, n Î N, НОД(m, n) = 1}. Представим множество Q _>0 в виде следующей таблицы 2.2.1:

Таблица 2.2.1

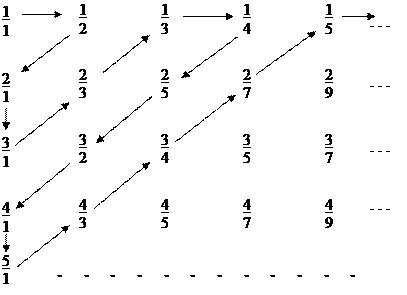
Обходя таблицу 2.2.1 по направлению стрелок, начиная от 1/1 = 1, приходим к последовательности 1, 1/2, 2, 3, 2/3, 1/3, 1/4, 2/5, 3/2, 4, 5, 4/3, 3/4, 2/7, 1/5,…, позволяющей занумеровать все эти числа. Обход таблицы можно осуществить и другими способами, например, по «квадратам». Итак, задано правило, по которому каждому числу q Î Q _>0 ставится в соответствие единственное число n Î N, являющееся номером q в данной последовательности. И для любого числа n Î N существует единственное число q Î Q _>0 такое, что q имеет номер n в данной последовательности. Итак, Q _>0 равномощно N.

Теперь рассмотрим множество всех рациональных чисел Q. Было показано выше, что Q _>0 = { q ₁, q ₂, q ₃,…, q_m,…} = { q_i | i Î N }. Обозначим теперь q ₀ число 0. Построим взаимно однозначное соответствие f: Q ® N следующим образом, как показано на рис. 2.2.2.

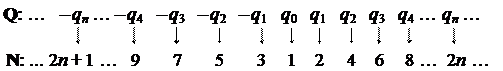Рис. 2.2.2

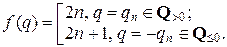
Из приведенных примеров видно одно из замечательных свойств бесконечных множеств, которое не имеет места в случае конечных множеств, – возможность приведения во взаимно однозначное соответствие бесконечного множества с его же бесконечным подмножеством.

Объединение конечного числа счетных множеств A ₁, A ₂,…, A_k, k Î N, счетно. Действительно, перенумеруем сначала все первые элементы множеств, затем вторые и т.д. Объединение счетного множества конечных множеств также счетно (сначала нумеруем все элементы первого множества, затем все элементы второго множества и т.д.). Из последнего утверждения следует, что множество всех слов в любом конечном алфавите счетно. Менее очевидно, что счетно и объединение счетного множества счетных множеств. Примером такого объединения является множество 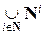всех векторов с натуральными компонентами, где N ⁱ – множество таких векторов длиной i.

Определение 2.2.6. Если бесконечное множество не равномощно множеству N, то такое множество называется несчетным.

Существование несчетных множеств следует из теоремы, доказанной в 1874 г. известным немецким математиком Георгом Кантором (1845–1918).

Теорема 2.2.5 (Г. Кантор). Множество всех действительных чисел интервала (0; 1) несчетно.

Заметим, что любое число рассматриваемого интервала представляет собой конечную или бесконечную десятичную дробь вида 0, a ₁ a ₂ a ₃… и может быть представлено точкой интервала вещественной оси. Предположим, что множество всех вещественных чисел интервала (0; 1) счетно (это множество является бесконечным) и существует нумерация чисел данного множества. Расположим все числа, представленные бесконечными десятичными дробями (если дробь конечна, то, начиная с некоторого номера, в ее десятичных разрядах записываются только нули), в порядке этой нумерации:

0, a ₁₁ a ₁₂ a ₁₃…

0, a ₂₁ a ₂₂ a ₂₃…

0, a ₃₁ a ₃₂ a ₃₃…

………………

Рассмотрим любую бесконечную десятичную дробь 0, b ₁ b ₂ b ₃… такую, что b ₁ ¹ a ₁₁, b ₂ ¹ a ₂₂, b ₃ ¹ a ₃₃ и т.д. Эта дробь не может войти в указанную последовательность, так как от первого числа она отличается первой цифрой, от второго числа – второй цифрой и т.д. Следовательно, все вещественные числа интервала (0; 1) не могут быть пронумерованы и данное множество несчетно.

Определение 2.2.7. Мощность множества всех действительных чисел интервала (0; 1) называется континуум, множества такой мощности называются континуальными. Метод, использованный при доказательстве теоремы 2.2.5, называется диагональным методом Кантора.

Необычные свойства несчетных множеств проявляются в том, что рассмотренный интервал (0; 1) может быть приведен во взаимно однозначное соответствие с полуинтервалами [0; 1) (рис. 2.2.3), (0; 1], отрезком [0; 1], а также множествами (a; b), (a; b ], [ a; b), [ a; b ], где a, b Î R, a < b, и всем множеством R.

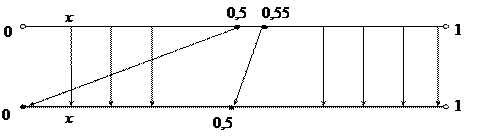
Рис. 2.2.3

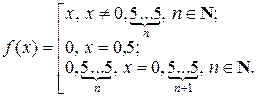
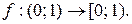
Аналогично доказывается, что (0; 1) «(0; 1], (0; 1] «[0; 1], [0; 1) «[0; 1]. Поэтому (0; 1) «[0; 1].

На рис. 2.2.4 приведено непосредственное доказательство того, что (0; 1) «[0; 1].

Рис. 2.2.4

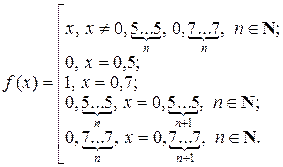
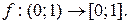
Аналогично можно показать, что (a; b) «(a; b ], (a; b) «[ a; b), (a; b ] «[ a; b ], [ a; b) «[ a; b ], (a; b) «[ a; b ] для произвольных a, b Î R таких, что a < b.

Взаимно однозначное соответствие (0; 1) «(a; b) можно осуществить с помощью центральной проекции (рис. 2.2.5).

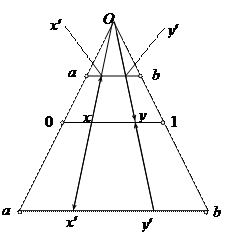Рис. 2.2.5

Это же соответствие можно задать аналитически: f (x) = (b – a) x + a, " x Î (0; 1). В общем случае взаимно однозначное соответствие (c; d) «(a; b), " a, b, c, d Î R, a < b, c < d, задается следующим образом:

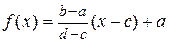, " x Î (c; d).

Таким образом, (0; 1) «(– p /2; p /2). Рассмотрим биекцию f: (– p /2; p /2) ® R, где f (x) = tg x, " x Î (– p /2; p /2). Получаем, что (– p /2; p /2) «R. Итак, (0; 1) «R и R является континуальным множеством.

Интервал (– p /2; p /2) можно представить полуокружностью длиной p. Тогда графически биекцию tg: (– p /2; p /2) ® R можно представить в виде центральной проекции, как показано на рис. 2.2.6.

Рис. 2.2.6

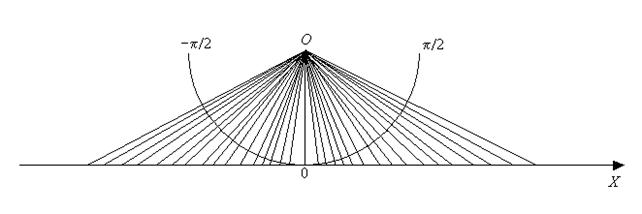
Г. Кантор доказал, что R ² «R и вообще R ⁿ «R для любого n Î N.

Множество всех подмножеств счетного множества континуально. Это становится ясным, если воспользоваться, как и в теореме 2.2.4, представлением подмножества в виде последовательности (но теперь уже бесконечной!) нулей и единиц: на i -ом месте стоит 1, если i -й элемент множества входит в данное подмножество, и 0 в противном случае. Получаем взаимно однозначное соответствие между собственными подмножествами счетного множества и правильными двоичными дробями, все множество которых, в свою очередь, взаимно однозначно соответствует множеству всех вещественных чисел полуинтервала [0; 1). Как показывается в теории множеств (с помощью метода, аналогичного диагональному методу Кантора), для множества любой мощности его булеан имеет более высокую мощность. Поэтому не существует множества максимальной мощности. Хорошо известным в истории математики является парадокс Кантора «Множество всех множеств». По смыслу своего описания оно должно содержать все мыслимые множества и, следовательно, иметь максимальную мощность, что противоречит результатам теории множеств. Однако само это «множество всех множеств» содержится в своем булеане в качестве элемента и поэтому не может иметь максимальную мощность. И, таким образом, кажущееся противоречие разрешается.

Дата добавления: 2014-01-05