Передача энергии от двухполюсников нагрузке

Если нагрузка R подключена к активному двухполюснику А (рис А), то в цепи возникнет ток I и будет выделяться мощность Р:

J=Uавхх/(R+Rвх); P=J^2*R=(U²авхх/(R+Rвх)²)*R (1)

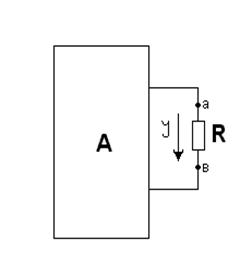
U_{ав ХХ} в формуле (1) – напряжение холостого хода на зажимах АВ. (Это такое напряжение U_авХХ=E₁, которое включенное в выделенную ветвь формирует в ней ток равный нулю J₁=0 т.е. по 2 закону Кирхгофа:

J₁R-U_ав = -Е₁.

J₁ = (U_{ав ХХ} - Е₁)/R=0 →U_{ав ХХ}=Е₁.

(подробнее смотри Бессонов стр.20).

R_вх в формуле (1) - входное сопротивление двухполюсника. Вспомним формулу для тока в некоторой ветви n, линейной электрической цепи, полученной с помощью метода наложения:

J_n=q_n1*E₁+q_n2*E₂+…+q_nn*E_n+…+q_nm*E

где q – проводимость, Е – ЭДС. і – ветви, q_nn – называется входной проводимостью ветви n. R=1/q_nn – входное сопротивление, q _nm – называется взаимной проводимостью ветвей n и m.

С другой стороны, мы можем записать:

q_nn=1/R_nn =J_n/U_n

т.е. входная проводимость любой ветви определяется отношением ЭДС. в этой ветви при равных нулю Е_j=0 (j≠n) всех остальных ветвей.

Другими словами, входная проводимость равна току, который потечет в ветви n, при включенном в неё ЭДС Е_n =1.

Определим, каково должно быть соотношение между сопротивлением на-грузки R и входным сопротивлением двухполюсника R_вх, чтобы в R выделилась максимальная мощность, чему она равна и каков при этом КПД передачи. С этой целью определим первую производную Р по R и приравниваем её к нулю:

dP = (R+R_вх)²-2R(R+R_вх) = 0 (2)

dR (R+R_вх)⁴

отсюда: R=R_вх (2а)

Определив вторую производную получим, что d²P/dR²<0, т.е. мы нашли максимум функции P=f(R), подставим (2) в (1), получим:

P_max=U²_авхх/4R_вх (3)

P_полн= U_авхх*J= U²_авхх/(R_вх +R) (4)

КПД. η =P/P_полн= R/(R_вх +R) (5)

Если R=R_вх, то η =0,5.

Если мощность P значительная, то работать с таким низким КПД недопустимо. Для малых мощностей P (милливатт) такие схемы недопустимы.

Выбор сопротивления нагрузке R, равного входному сопротивлению R_вх активного двухполюсника, называют согласованием нагрузки.

Схема линии передачи показана ниже, где R₁ – сопротивление линии

передачи, R₂ - сопротивление нагрузки, U₁ – напряжение источника энергии Е в начале линии. Тогда:

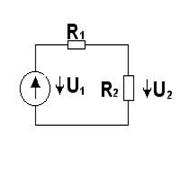P₁=U₁*J

P₂=U₁*J-J²*R₁

. η = P₂ / P₁=1-R₁*J/U₁= R₁/R₁+R₂

U₂= U₁-R₁*J

J_max=U₁/R₁ (R₂=0)

(Подробнее смотри Бессонова стр.40).

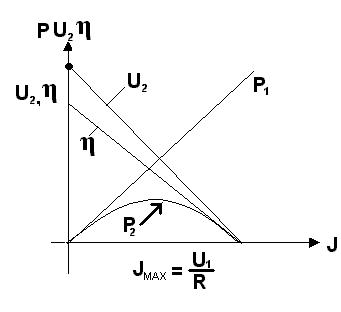
Т.о. КПД тем выше, чем выше U₁ – Напряжение в начале линии. На рис. ниже показано зависимость P₁, P₂, КПД.,U₂, как функция тока по линии при неизмененном напряжении на входе линии U₁ и при неизменном R₁.

Дата добавления: 2014-01-05