
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические указания по теме. Методику расчетов при выборочном наблюдении рассмотрим на примере 10 %-й бесповторной выборки производственных фирм района с целью определения с вероятностью
|
|
|
|
Методику расчетов при выборочном наблюдении рассмотрим на примере 10 %-й бесповторной выборки производственных фирм района с целью определения с вероятностью 0,954 средней стоимости их товарной продукции. В табл. 1.3. приведены выборочные данные и промежуточные расчеты.
Таблица 1.3
Выборочные данные о товарной продукции фирм и промежуточные расчеты
| Xi, млн. руб. | fi, фирм | Xи | Xиfi | Хи-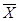
| (Хи -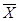 )2 )2
| (Хи -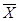 )2 fi )2 fi
|
| до 3 | -14,9 | 222,01 | 1110,05 | |||
| 3-5 | -12,9 | 166,41 | 2496,15 | |||
| 5-10 | 7,5 | -9,4 | 88,36 | 2120,64 | ||
| 10-30 | 3,1 | 9,61 | 384,4 | |||
| 30 и более | 23,1 | 533,6 | 8537,76 | |||
| Итого | — | — | — | 14649,02 |
В этой таблице первые два столбца представляют собой результаты интервальной группировки выборочных данных, а в остальных столбцах на ее основе выполнены необходимые расчеты, аналогично предыдущим методическим указаниям.
Так, по формуле (1.14) определена средняя выборочная стоимость
товарной продукции
 = 1690 /100 = 16,9 млн. руб.
= 1690 /100 = 16,9 млн. руб.
Затем по формуле (1.25) определяется выборочная дисперсия
Дв= 14649 /100 = 146,49 млн. руб2.
Теперь по формуле (1.36) можно вычислить среднюю ошибку бесповторной выборки
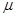 =
= 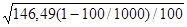 = 1,148 (млн.руб).
= 1,148 (млн.руб).
При этом общее число фирм N = 1000, т.к. по условию выбранные 100 фирм составляет 10% от общего числа (элементарная задачка на проценты).
Наконец, по формуле (1.38) находим предельную ошибку выборки, учитывая, что при заданной вероятности 0,954 коэффициент доверия равен 2. То есть  = 2*1,148 = 2,3 млн. руб.
= 2*1,148 = 2,3 млн. руб.
Следовательно, средняя стоимость товарной продукции всех фирм района с вероятностью 0,954 находится в доверительном интервале
(16,9-2,3) 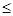
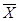
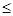 (16,9+2,3) или 14,6 млн. руб.
(16,9+2,3) или 14,6 млн. руб. 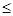
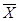
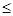 19,2 млн. руб.
19,2 млн. руб.
Далее рассмотрим методику расчета доверительного интервала по альтернативному признаку, поставив цель определения в районе доли фирм с товарной продукцией до 10 млн. руб.
Из табл. 1.3 находим, что выборочная доля таких фирм составляет
w = (5+15+24)/100 = 0,44.
Выборочная дисперсия по формуле (1.37) равняется
Дв = 0,44(1 -0,44) = 0,246.
Тогда средняя ошибка бесповторной выборки по формуле (1.36) составит
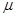 =
= 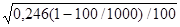 = 0,047.
= 0,047.
Наконец, предельная ошибка по формуле (1.38) с учетом того, что при вероятности 0,954 коэффициент доверия 2, будет равна  = 2*0,047= 0,094.
= 2*0,047= 0,094.
Значит, в районе доля фирм с товарной продукцией до 10 млн. руб. при вероятности 0,954 находится в доверительном интервале
(0,44-0,094) 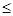 р
р 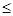 (0,44+0,094) или 0,346
(0,44+0,094) или 0,346 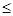 р
р 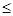 0,534 или 34,6%
0,534 или 34,6% 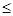 р
р 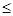 53,4%.
53,4%.
Отметим, что в случае представления выборочных данных в дискретном виде отпадает необходимость нахождения середин интервалов, что исключает третий столбец табл. 1.3. В остальных столбцах следует вместо Xи использовать Xi.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 277; Нарушение авторских прав?; Мы поможем в написании вашей работы!