Математическое описание элементов и систем

Для анализа САР необходимо её математическое описание. Система разделяется на элементы и составляются уравнения, описывающие их поведение (рассмотрим только стационарные САР – у которых свойства элементов не изменяются с течением времени). Обычно это обыкновенные дифференциальные уравнения с постоянными коэффициентами. Нелинейные дифференциальные уравнения заменяются приближенными линейными (так называемая линеаризация).

2.1. Преобразование Лапласа и передаточная функция элемента.

Метод преобразования Лапласа позволяет заменить достаточно сложное решение дифференциальных уравнений относительно простым решением алгебраических уравнений.

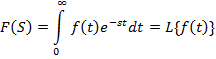
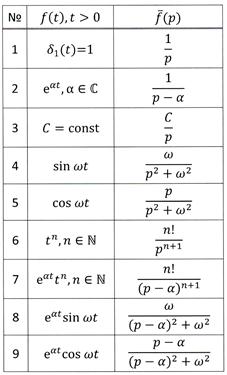
При решении большинства практических задач используются таблицы преобразований Лапласа, вида:

Переменная P (оператор Лапласа) может рассматриваться как оператор дифференцирования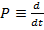

Дифференциальное уравнение → Преобразование Лапласа → Алгебраическое уравнение

Передаточной функцией элемента называется отношение преобразования Лапласа, его выходной величины, к преобразованию Лапласа выходной величины при нулевых начальных условиях. Поэтому при нулевых начальных условиях по Лапласу сначала преобразуется дифференциальное уравнение этого элемента.

Примеры вычисления передаточной функции элементов САР по их дифференциальным уравнениям:

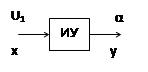
1) Усилитель

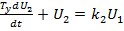
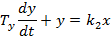
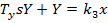
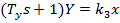
Передаточная функция:

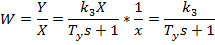
Полезно запомнить, что при нулевых начальных условиях:

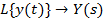
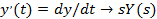
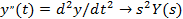
2) Двигатель

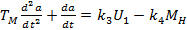
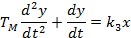
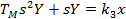
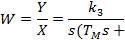
3) Предварительный усилитель напряжения

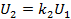
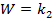
В общем случае передаточная функция есть отношение двух полиномов от S:

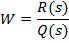
где полиномы Q и R степени n и 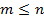соответственно.

Удобно определить W в виде отношения нормир. полиномов (т.е. полиномов у которых коэффициент при младшем члене равен 1), умноженного на постоянный коэффициент.

Q – называется характеристическим полиномом, а его корни – полюсами передаточной функции. Корни полюса R – нули передаточной функции.

2.2. Структурные схемы и простейшие структурные преобразования.

Структурная схема САР – её условное графическое изображение в виде соединенных динамических звеньев с указанием внешних воздействий и воздействий эл-тов друг на друга.

· Динамическое звено:

Внутри указывается передаточная функция

·

· Пример структурной схемы САР:

·

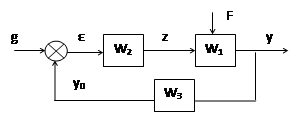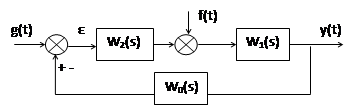Структурная схема САР используется для определения её передаточной функции. Обычно структурная схема приводится к эквивалентной одноконтурной вида:

Для этого пользуются правилами структурных преобразований, например:

Последовательное соединение

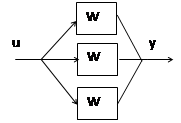Параллельное соединение

2.3. Передаточные функции САР

Для расчетов обычно необходимы, определяемые по структурной схеме САР.

· передаточная функция разомкнутой САР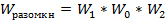

· передаточная функция замкнутой САР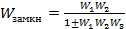

Относительно задающего воздействия и относительно возмущения и ошибки слежения.

2.4. Временные и частотные характеристики САР.

Часто имеет место резкое изменение внешнего воздействия на САР (вкл. и выкл. потребителей электроэнергии и тд.) и важно оценить поведение САР в таких критических ситуациях – выяснить насколько значительным будет отклонение от нормального режима и насколько быстро и точно оно будет устранено регулятором.

Рассмотрим единичную структурную функцию:

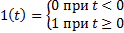
Реакцию элемента или системы при нулевых начальных условиях на входную величину, являющийся единичной ступенчатой функцией времени, называют переходной характеристикой h элемента или системы.

Помимо оценки поведения САР (эл-та САР) в переходном режиме следует изучить её поведение в установившемся режиме.

Пусть на вход линейного эл-та (системы) воздействует гармонический сигнал 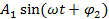той же угловой частоты, но с иными амплитудой и фазой. Отношение 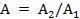и разность 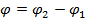являются функциями частоты и их называют амплитудно-частотной (АЧХ) и фазово-частотной (ФЧХ) характеристиками САР (эл-та САР) соответственно.

Обычно используют логарифмические частотные характеристики ЛАЧХ и ЛФЧХ.

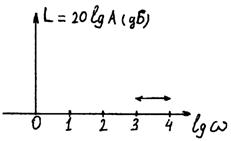
Построение асимптотической ЛАЧХ.

Участки ЛАЧХ могут быть заменены прямыми – асимптотами с наклоном, кратным 20 дБ/дек: 0 дБ/дек, +20 дБ/дек, -20 дБ/дек, +40 дБ/дек и др. Каждой сопрягающей частоте 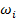, при которой наклон ЛАЧХ изменяется на 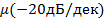соответствует множитель 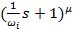в знаменателе передаточной функции. Если при сопрягающей частоте 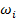наклон ЛАЧХ изменился на η(+20дБ/дек), то ей соответствует множитель 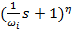в числителе.

Примеры построения:

1)

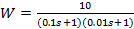
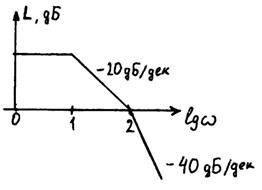Сопряг. частоты

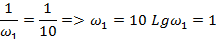
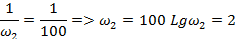
20Lg k =20 Lg10 = 20дБ

2)

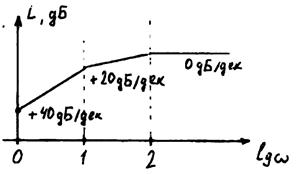
20Lg k = 20дБ

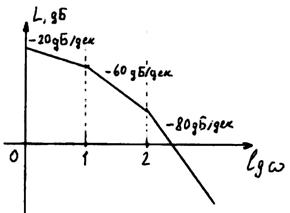
3)

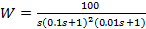
20Lg k = 20Lg100 = 20*2=40Дб

Дата добавления: 2014-01-05