Основы финансовых вычислений

Временная стоимость денег

Які властивості має блок тексту і графіки?

Що таке успадкування?

Що таке групування?

Які ви знаєте псевдокласи першої групи?

Що визначають псевдокласи?

Які типи селекторів ви знаєте?

Селектор за елементом, селектор за класом, селектор за ідентифікатором, контекстний селектор.

6. Для чого застосовується псевдоелемент after?

Псевдоелемент after застосовується для вставки призначеного контенту після елемента. Цей псевдоелемент працює спільно з сталевою властивіс­тю content, котра визначає контент для вставки.

7. Для чого використовується псевдоелемент before?

Псевдоелемент before за своєю дією аналогічний до псевдоелемента after, але вставляє контент до елемента. Застосовується переважно для додавання мар­керів до списків.

8. Що таке буквиця?

Буквиця - збільшена перша літера абзацу, базова лінія якої розташова­на нижче на один або декілька рядків від базової лінії основного тексту.

Псевдокласи визначають виведення у вікні браузера елементів, які змі­нюються з часом або в результаті дій користувача, наприклад, гіпертекстове посилання, яке змінює свій колір при наведенні на нього курсора миші, а та­кож положення в дереві документа.

Псевдокласи першої групи:

active - застосування стилю відбувається при активації користувачем елемента. Наприклад, при наведенні курсору на посилання та натисканні лі­вої кнопки миші;

Ііnк - застосовується до невідвіданого посилання, тобто посилання, на яке користувач ще не натискав.

focus - застосовується до елемента при отриманні ним фокусу. Напри­клад, для форми - текстового рядка отримання фокусу означає, що курсор встановлено в полі, і за допомогою клавіатури можна вводити в нього текст;

Групування - об'єднання селекторів з однаковими оголошеннями з ме­тою зменшення загального об'єму та впорядкування коду.

Успадкування - це перенесення правил форматування для елементів, що знаходяться всередині інших.

Блок тексту та графіки має властивості: висоту (height;), ширину (width), рaмки(border), зовнішні відступи (margin), внутрішні відступи (padding), кон­тур (outline), розміщення та обтікання (float), керування обтіканням (clear).

Одним из важнейших свойств денежных потоков является их распределенность во вре­мени. При анализе относительно краткосрочных периодов (до 1 года) в условиях стабильной экономики данное свойство оказывает относительно незначительное влияние, которым часто пренебрегают. Определяя годовой объем реализации по предприятию, просто складывают суммы выручки за каждый из месяцев отчетного года. Аналогично поступают со всеми осталь­ными денежными потоками, что позвляет оперировать их итоговыми значениями. Однако в случае более длительных периодов или в условиях сильной инфляции возникает серьезная про­блема обеспечения сопоставимости данных. Одна и та же номинальная сумма денег, получен­ная предприятием с интервалом в 1 и более год, в таких условиях будет иметь для него неоди­наковую ценность. Очевидно, что 1 млн. рублей в начале 1992 года был значительно весомее миллиона «образца» 1993 и более поздних лет. Как правило, в таких случаях производят кор­ректировку отчетных данных с учетом инфляции. Но проблема не сводится только к учету ин­фляции. Одним из основополагающих принципов финансового менеджмента является призна­ние временной ценности денег, то есть зависимости их реальной стоимости от величины про­межутка времени, остающегося до их получения или расходования. В экономической теории данное свойство называется положительным временным предпочтением.

Наряду с инфляционным обесцениванием денег существует еще как минимум три важ­нейшие причины данного экономического феномена. Во-первых, «сегодняшние» деньги всегда будут ценнее «завтрашних» из-за риска неполучения последних, и этот риск будет тем выше, чем больше промежуток времени, отделяющий получателя денег от этого «завтра». Во-вторых, располагая денежными средствами «сегодня», экономический субъект может вложить их в ка­кое-нибудь доходное предприятие и заработать прибыль, в то время как получатель будущих денег лишен этой возможности. Расставаясь с деньгами «сегодня» на определенный период времени (допустим, давая их взаймы на 1 месяц), владелец не только подвергает себя риску их невозврата, но и несет реальные экономические потери в форме неполученных доходов от ин­вестирования. Кроме того снижается его платежеспособность, так как любые обязательства, по­лучаемые им взамен денег, имеют более низкую ликвидность, чем «живые» деньги. То есть у кредитора возрастает риск потери ликвидности, и это третья причина положительного времен­ного предпочтения. Естественно, большинство владельцев денег не согласны бесплатно прини­мать на себя столь существенные дополнительные риски. Поэтому, предоствляя кредит, они ус­танавливают такие условия его возврата, которые по их мнению полно­стью возместят им все моральные и материальные неудобства, возникающие у человека, расстающегося (пусть даже и временно) с денежными знаками.

Количественной мерой величины этого возмещения является процентная ставка. С ее по­мощью может быть определена как будущая стоимость «сегодняшних» денег (например, если их собираются ссудить), так и настоящая (современная, текущая или приведенная) стоимость «завтрашних» денег – например, тех, которыми обещают расплатиться через год после по­ставки товаров или оказания услуг. В первом случае говорят об операции наращения, поэтому будущую стоимость денег часто называют наращенной. Во втором случае выполняется дискон­тирование или приведение будущей стоимости к ее современной величине (текущему моменту) – отсюда термин дисконтированная, приве­денная или текущая стоимость. Операции наращения денег по процентной ставке более просты и понятны, так как с ними приходится сталкиваться довольно часто беря или давая деньги взаймы. Однако для финансового менеджмента значи­тельно более важное значение имеет дисконтирование де­нежных потоков, приведение их бу­дущей стоимости к со­временному моменту времени для обеспечения сопоставимости величины распределенных по времени платежей. В принципе, дисконтирование – это наращение «наобо­рот», однако для фи­нансовых расчетов важны детали, поэтому необходимо более подробно рассмотреть как пря­мую, так и обратную задачу процент­ных вычислений. Прежде чем рассмат­ривать их примени­тельно к денежным потокам, следует усвоить наиболее элементарные опера­ции с единичными суммами (разовыми платежами).

Процентная ставкапоказывает степень интенсивности изменения стоимости денег во вре­мени. Абсолютная величина этого изменения называется процентом, измеряется в де­нежных единицах (например, рублях) и обозначается I. Если обозначить будущую сумму S, а совре­менную (или первоначальную) P, то I = S – P. Процентная ставка i является относи­тельной ве­личиной, измеряется в десятичных дробях или %, и определяется делением процентов на первоначальную сумму:

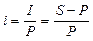(1)

Можно заметить, что формула расчета процентной ставки идентична расчету статистического показателя «темп прироста». Действительно, если абсолютная сумма процента (I) представляет собой прирост современной величины, то отношение этого прироста к самой современной ве­личине и будет темпом прироста перовначальной суммы. Наращение первоначальной суммы по процентной ставке называется декурсивным мето­дом начисления процентов.

Кроме процентной существует учетная ставка d (другое название – ставка дисконта), ве­личина которой определяется по формуле:

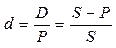, (2)

где D – сумма дисконта.

Сравнивая формулы (2) и (3) можно заметить, что сумма процентов I и величина дисконта D определяются одинаковым образом – как разница между будущей и современной стоимостями. Однако, смысл, вкладываемый в эти термины неодинаков. если в первом случае речь идет о приросте текущей стоимости, своего рода «наценке», то во втором определяется снижение бу­дущей стоимости, «скидка» с ее величины. (Diskont в переводе с немецкого означает «скидка»). Неудивительно, что основной областью применения учетной ставки является дисконтирование, процесс, обратный по отношению к начислению процентов. Тем не менее, иногда она исполь­зуется и для наращения. В этом случае говорят об антисипа­тивных процентах.

При помощи рассмотренных выше ставок могут начисляться как простые так и сложные проценты. При начислении простых процентов наращение первоначальной суммы происхо­дит в арифметической прогрессии, а при начислении сложных процентов – в геометрической. Вна­чале более подробно рассмотрим операции с простыми процентами.

Начисление простых декурсивных и антисипативных процентов производится по различным формулам:

декурсивные проценты: 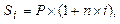(3)

антисипативные проценты: , (4)

где n – продолжительность ссуды, измеренная в годах.

Для упрощения вычислений вторые сомножители в формулах (3) и (4) называются множителями наращения простых процентов: (1 + ni) – множитель наращения декурсивных процентов; 1 / (1 – nd) – множитель наращения антисипативных процентов.

Например, ссуда в размере 1 млн. рублей выдается сроком на 0,5 года под 30% годовых. В слу­чае декурсивных процентов наращенная сумма (S_i) будет равна 1,15 млн. рублей (1 * (1 + 0,5 * 0,3), а сумма начисленных процентов (I) – 0,15 млн. рублей (1,15 – 1). Если же начислять про­центы по ан­тисипативному методу, то наращенная величина (S_d) составит 1,176 млн. рублей (1 * (1 / (1 – 0,5 * 0,3), а сумма процентов (D) 0,176 млн. рублей. Наращение по антисипативному методу всегда происходит более быстрыми темпами, чем при использовании процентной ставки. Поэтому банки используют этот метод для начисления процентов по выдаваемым ими ссудам в периоды высокой инфляции. Однако у него есть существенный недостаток: как видно из формулы (4), при n = 1 / d, знаменатель дроби обращается в нуль и выражение теряет смысл.

Вообще, начисление процентов с использованием ставки, предназначенной для выполнения прямо противоположной операции – дисконтирования – имеет оттенок некой «не­естественности» и иногда порождает неразбериху (аналогичную той, которая может возникнуть у розничного торговца, если он перепутает правила определения скидок и наценок на свои то­вары). С позиции математики никакой сложности здесь нет, преобразовав (1), (2) и (4), получаем:

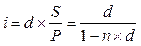(5)

Соблюдая это условие, можно получать эквивалентные результаты, начисляя проценты как по формуле (3), так и по формуле (4).

Антисипативным методом начисления процентов обычно пользуются в чисто технических целях, в частности, для определения суммы, дисконтирование которой по заданным учетной ставке и сроку, даст искомый результат. В следующем параграфе будут рассмотрены конкретные примеры возникнове­ния подобных ситуаций.

Как правило, процентные ставки устанавливаются в годовом исчислении, поэтому они назы­ваются годовыми. Особенностью простых процентов является то, что частота процессов нараще­ния в течение года не влияет на результат. То есть нет никакой разницы начислять 30% годовых 1 раз в год или начислить 2 раза по 15% годовых. Простая ставка 30% годовых при одном начислении в году называется эквивалентной простой ставке 15% годовых при начислении 1 раз в полгода. Данное свойство объясняется тем, что процесс наращения по про­стой процентной ставке представляет собой арифметическую прогрессию с первым членом a₁ = P и разностью d = (P * i).

P, P + (P * i), P + 2 * (P * i), P + 3 * (P * i), …, P + (k – 1) * (P * i)

Наращенная сумма S есть ничто иное как последний k-й член этой прогрес­сии (S = a_k = P + n * P * i), срок ссуды n равен k – 1. Поэтому, если увеличить n и одновременно пропорционально уменьшить i, то величина каждого члена погрессии, в том числе и последнего, останется неиз­менной.

Однако продол­жительность ссуды (или другой финансовой операции, связанной с начис­ле­нием процентов) n не­обязательно должна равняться году или целому числу лет. Напротив, про­стые проценты чаще всего используются при краткосрочных (длительностью менее года) опера­циях. В этом случае возникает проблема определения длительности ссуды и про­должитель­ности года в днях. Если обозначить продолжительность года в днях буквой K (этот показатель называется временная база), а количество дней пользования ссудой t, то использо­ванное в формулах (3) и (4) обозначение количества полных лет n можно будет выразить как t/K. Подставив это выра­жение в (3) и (4), получим:

для декурсивных процентов: (6)

для антисипативных процентов: 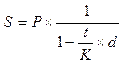, (7)

В различных случаях могут применяться различные способы подсчета числа дней в году (соглашение по подсчету дней). Год может приниматься равным 365 или 360 дням (12 полных ме­сяцев по 30 дней в каждом). Проблема усугубляется наличием високосных лет. Например, обозна­чение ACT/360 (actual over 360) указывает на то, что длительность года принимается равной 360 дням. Однако возникает вопрос, а как при этом определяется продолжительность ссуды? Например, если кредит выдается 10 марта со сроком возврата 17 июня этого же года, как считать его длительность – по календарю или исходя из предположения, что любой месяц равен 30 дням? Безусловно, в каждом конкретном случае может быть выбран свой оригинальный способ подсчета числа дней, однако на практике выработаны некоторые общие принципы, знание которых может помочь сориентироваться в любой конкретной ситуации.

Если временная база (K) принимается равной 365 (366) дням, то проценты называются точ­ными. Если временная база равна 360 дням, то говорят о коммерческих или обыкновенных про­центах. В свою очередь подсчет длительности ссуды может быть или приближенным, когда исхо­дят из продолжительности года в 360 дней, или точным – по календарю или по специаль­ной таб­лице номеров дней в году. Определяя приближенную продолжительность ссуды, сна­чала подсчи­тывают число полных месяцев и умножают его на 30. Затем добавляют число дней в не­полных ме­сяцах. Общим для всех способов подсчета является правило: день выдачи и день воз­врата кредита считаются за 1 день (назовем его граничный день). В приведенном выше ус­лов­ном примере точная длительность ссуды составит по календарю 99 дней (21 день в марте + 30 дней в апреле + 31 день в мае + 16 дней в июне + 1 граничный день). Тот же результат будет получен, если использовать таблицу номеров дней в году (10 марта имеет порядковый номер 69, а 17 июня – 168). Если же ис­пользовать приближенный способ подсчета, то длительность ссуды составит 98 дней (21 + 2 * 30 + 16 + 1).

Наиболее часто встречаются следующие комбинации временной базы и длительности ссуды (цифры в скобках обозначают соответственно величину t и K):

1. Точные проценты с точным числом дней (365/365).

2. Обыкновенные (коммерческие) проценты с точной длительностью ссуды (365/360).

3. Обыкновенные (коммерческие) проценты с приближенной длительностью ссуды (360/360).

Различия в способах подсчета дней могут показаться несущественными, однако при больших суммах операций и высоких процентных став­ках они достигают весьма приличных раз­ме­ров. Предположим, что ссуда в размере 10 млн. рублей выдана 1 мая с возвратом 31 де­кабря этого года под 45% годовых (простая процентная ставка). Определим наращенную сумму этого кре­дита по каждому из трех способов. Табличное значение точной длительности ссуды равно 244 дня (365 – 121); приближенная длительность – 241 день (6 * 30 + 30 + 30 + 1).

1. 10 * (1 + 0,45 * 244/365) = 13,008 млн. рублей

2. 10 * (1 + 0,45 * 244/360) = 13,05 млн. рублей

3. 10 * (1 + 0,45 * 241/360) = 13,013 млн. рублей

Разница между наибольшей и наименьшей величинами (13,05 – 13,008) означает, что должник бу­дет вынужден заплатить дополнительно 42 тыс. рублей только за то, что согласился (или не об­ратил внимания) на применение 2 способа начисления процентов.

Обратной задачей по отношению к начислению процентов является расчет современной стоимости будущих денежных поступлений (платежей) или дисконтирование. В ходе дискон­тиро­вания по известной будущей стоимости S и заданным значениям процентной (учетной) ставки и длительности операции находится первоначальная (современная, приведенная или те­кущая) стои­мость P. В зависимости от того, какая именно ставка – простая процентная или про­стая учетная – применяется для дисконтирования, различают два его вида: математическое дис­контирование и банковский учет.

Метод банковского учета получил свое название от одноименной финансовой операции, в ходе которой коммерческий банк выкупает у владельца (учитывает) простой или переводный век­сель по цене ниже номинала до истечения означенного на этом документе срока его погаше­ния. Разница между номиналом и выкупной ценой образует прибыль банка от этой операции и называ­ется дисконт (D). Для определения размера выкупной цены (а следовательно, и суммы дисконта) применяется дисконтирование по методу банковского учета. При этом используется простая учет­ная ставка d. Выкупная цена (современная стоимость) векселя определяется по формуле:

(8)

где t – срок, остающийся до погашения векселя, в днях. Второй сомножитель этого выражения (1 – (t / k) * d) называется дисконтным множителем банковского учета по простым процентам. Как правило, при банковском учете применяются обык­но­вен­ные проценты с точной длительностью ссуды (2 вариант). Например, владелец векселя номина­лом 25 тыс. рублей обратился в банк с предложением учесть его за 60 дней до наступления срока погашения. Банк согласен выполнить эту операцию по простой учетной ставке 35% годо­вых. Выкупная цена векселя составит:

P = 25000 * (1 – 60/360 * 0,35) = 23541,7 руб.,

а сумма дисконта будет равна

D = S – P = 25000 – 23541,7 = 1458,3 руб.

При математическом дисконтировании используется простая процентная ставка i. Расчеты выполняются по формуле:

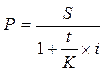(9)

Выражение 1 / (1 + (t / k) * i) называется дисконтным множителем математического дисконтирования по простым процентам.

Этот метод применяется во всех остальных (кроме банковского учета) случаях, когда возникает необходимость определить современную величину суммы денег, которая будет получена в бу­ду­щем. Например, покупатель обязуется оплатить поставщику стоимость закупленных товаров через 90 дней после поставки в сумме 1 млн. рублей. Уровень простой процентной ставки со­ставляет 30% годовых (обыкновенные проценты). Следовательно текущая стоимость това­ров будет равна:

P = 1 / (1 + 90 / 360 * 0,3) = 0,93 млн. рублей

Применив к этим условиям метод банковского учета, получим:

P = 1 * (1 – 90 / 360 * 0,3) = 0,925 млн. рублей

Второй вариант оказывается более выгодным для кредитора. Следует помнить, что каких-то жестких требований выбора того либо иного метода выполнения финансовых расчетов не су­ществует. Никто не может запретить участникам финансовой операции выбрать в данной си­туации метод математического дисконтирования или банковского учета. Существует, пожалуй, единственная закономерность – банками, как правило, выбирается метод, более выгодный для кредитора (инвестора).

Основной областью применения простых процентной и учетной ставок являются кратко­срочные финансовые операции, длительность которых менее 1 года. Вычисления с простыми ставками не учитывают возможность реинвестирования начисленных процентов, потому что на­ращение и дисконтирование производятся относительно неизменной исходной суммы P или S. В отличие от них сложные ставки процентов учитывают возможность реинвестирования про­центов, так как в этом случае наращение производится по формуле не арифметической, а гео­метрической прогрессии, первым членом которой является начальная сумма P, а знаменатель равен (1 + i).

P, P * (1 + i), P * (1 + i)², P * (1 + i)³ , …, P * (1 + i)ⁿ,

где число лет ссуды n меньше числа членов прогрессии k на 1 (n = k – 1).

Наращенная стоимость (последний член прогрессии) находится по формуле:

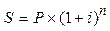(10),

где (1 + i) ⁿ – множитель наращения декурсивных сложных процентов.

С позиций финансового менеджмента использование сложных процентов является более предпочтительным, т.к. признание возможности собственника в любой момент инвестировать свои средства с целью получения дохода является краеугольным камнем всей финансовой теории. При использовании простых процентов эта возможность часто не учитыва­ется, поэтому результаты вычислений получаются менее корректными. Тем не менее при крат­косрочных финансовых операциях по-прежнему широко применяются вычисления простых процентов. Некоторые математики считают это досадным пережитком, оставшимся с тех пор, когда у финансистов не было под рукой калькуляторов и они были вынуждены прибегать к бо­лее простым, хотя и менее точным способам расчета. Представляется возможным и несколько иное объяснение данного факта. При длительности операций менее 1 года (n < 1) начисление простых процентов обеспечивает получение результатов даже более выгодных для кредитора, чем использование сложных процентов. Выше уже отмечалась закономерность выбора банками именно таких, более выгодных для кредитора способов. Поэтому было бы наивно недооцени­вать вычислительные мощности современных банков и интеллектуальный потенциал их со­трудников, полагая, что они используют грубые методы расчетов только из-за их низкой трудо­емкости. Трудно представить себе банкира, хотя бы на секунду забывающего о собственной вы­годе.

Сама по себе сложная процентная ставка i ничем не отличается от простой и рассчитыва­ется по такой же формуле (1). Сложная учетная ставка определяется по формуле (2). Так же как и в случае про­стых процентов возможно применение сложной учетной ставки для начисления процентов (ан­тисипативный метод):

, (11)

где 1 / (1 – d)^n – множитель наращения сложных антисипативных процентов.

Однако практическое применение такого способа наращения процентов весьма ограничено и он относится скорее к разряду финансовой экзотики.

Как уже отмечалось, наиболее широко сложные проценты применяются при анализе дол­госрочных финансовых операций (n > 1). На большом промежутке времени в полной мере про­является эффект реинвестирования, начисления «процентов на проценты». В связи с этим во­прос измерения длительности операции и продолжительности года в днях в случае сложных процентов стоит менее остро. Как правило, неполное количество лет выражают дробным чис­лом через количество месяцев (3/12 или 7/12), не вдаваясь в более точные подсчеты дней. По­этому в формуле начисления сложных процентов число лет практически всегда обозначается буквой n, а не выражением t/K, как это принято для простых процентов. Наиболее щепетильные кредиторы, принимая во вни­мание большую эффективность простых процентов на коротких отрезках времени, используют смешанный порядок начисления процентов в случае, когда срок операции (ссуды) не равен це­лому числу лет: сложные проценты начисляются на период, изме­ренный целыми годами, а про­центы за дробную часть срока начисляются по простой процент­ной ставке.

, (12)

где a – число полных лет в составе продолжительности операции,

t – число дней в отрезке времени, приходящемся на неполный год,

K –временная база.

В этом случае вновь возникает необходимость выполнения календарных вычислений по рас­смотренным выше правилам. Например, ссуда в 3 млн. рублей выдается 1 января 1997 года по 30 сентября 1999 года под 28% годовых (процентная ставка). В случае начисления сложных процентов за весь срок пользования деньгами наращенная сумма составит:

S = 3 * (1 + 0,28)^(2 + 9/12) = 5,915 млн. рублей

Если же использовать смешанный способ (например, коммерческие проценты с точным числом дней), то получим:

S = 3 * (1 + 0,28)^2 * (1 + 272 / 360 * 0,28) = 6 млн. рублей

Таким образом, щепетильность кредитора в данном случае оказалась вовсе не излишней и была вознаграждена дополни­тельным доходом в сумме 85 тыс. рублей.

Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года. Здесь опять сказывается влияние реинвестирования на­численных процентов: база начисления возрастает с каждым новым начислением, а не остается неизменной, как в случае простых процентов. Например, если начислять 20% годовых 1 раз в год, то первоначальная сумма в 1 тыс. рублей возрастет к концу года до 1,2 тыс. рублей (1 * (1+ 0,2)). Если же начислять по 10% каждые полгода, то будущая стоимость составит 1,21 тыс. руб­лей (1 * (1 + 0,1) * (1 + 0,1)), при поквартальном начислении по 5% она возрастет до 1,216 тыс. рублей. По мере увеличения числа начислений (m) и продолжительности операции эта разница будет очень сильно увеличиваться. Если разделить сумму начисленных процентов при еже­квартальном наращении на первоначальную сумму, то получится 21,6% (0,216 / 1 * 100), а не 20%. Следовательно сложная ставка 20% при однократном наращении и 20% (четыре раза по 5%) при поквартальном наращении приводят к различным результатам, то есть они не являются эквивалентными. Цифра 20% отражает уже не действительную (эффективную), а номинальную ставку. Эффективной процентной ставкой является значение 21,6%. В финансовых расчетах номинальную сложную процентную ставку принято обозначать буквой j. Формула наращения по сложным процентам при начислении их m раз в году имеет вид:

, (13)

Например ссуда размером 5 млн. рублей выдана на 2 года по номинальной сложной процентной ставке 35% годовых с начислением процентов 2 раза в год. Будущая сумма к концу срока ссуды составит:

S = 5 * (1 + 0,35 / 2)^(2 * 2) = 9,531 млн. рублей.

При однократном начислении ее величина составила бы лишь 9,113 млн. рублей (5 * (1 + 0,35)^2; зато при ежемесячном начислении возвращать пришлось бы уже 9,968 млн. рублей (5 * 1 + (0,35 / 12)^(12 * 2)).

При начислении антисипативных сложных процентов, номинальная учетная ставка обо­значается буквой f, а формула наращения принимает вид:

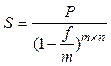(14)

Выражение 1 / (1 – f / m)^mn множитель наращения по номинальной учетной ставке.

Дисконтирование по сложным процентам также может выполняться двумя способами – математическое дисконтирование и банковский учет. Последний менее выгоден для кредитора, чем учет по простой учетной ставке, поэтому используется крайне редко. В случае однократ­ного начисления процентов его формула имеет вид:

, (15)

где (1 –d)ⁿ – дисконтный множитель банковского учета по сложной учетной ставке.

при m > 1 получаем

, (16)

где f – номинальная сложная учетная ставка,

(1 – f / m)^mn – дисконтный множитель банковского учета по сложной номинальной учетной ставке.

Значительно более широкое распространение имеет математическое дисконтирование по сложной процентной ставке i. Для m = 1 получаем

, (17)

где 1 / (1 + i)ⁿ – дисконтный множитель математического дисконтирования по сложной процентной ставке.

При неоднократном начислении процентов в течение года формула математического дисконти­рования принимает вид:

, (18)

где j –номинальная сложная процентная ставка,

1 / (1 + j / m)^mn – дисконтный множитель математического дисконтирования по сложной номинальной процентной ставке.

Например, требуется определить современную стоимость платежа в размере 3 млн. рублей, ко­торый должен поступить через 1,5 года, процентная ставка составляет 40%:

при m = 1 P = 3 / (1 + 0,4)^1,5 = 1,811 млн. рублей

при m = 2 (начисление 1 раз в полугодие) P = (3 / (1 + 0,4 / 2)^(2 * 1,5) = 1,736 млн. рублей

при m = 12 (ежемесячное начисление) P = (3 / (1 + 0,4 / 12)^(12 * 1,5) = 1,663 млн. рублей.

По мере увеличения числа начислений процентов в течение года (m) проежуток времени между двумя смежными начислениями уменьшается – при m = 1 этот промежуток равен 1 году, а при m = 12 – только 1 месяцу. Теоретически можно представить ситуацию, когда начисление сложных процентов производится настолько часто, что общее его число в году стремится к бес­конечнности, тогда величина промежутка между отдельными начислениями будет прибли­жаться к нулю, то есть начисление станет практически непрерывным. Такая на первый взгляд гипотетическая ситуация имеет важное значение для финансов и при построении сложных ана­литических моделей (например при разработке масштабных инвестиционных проектов) часто применяют непрерывные проценты. Непрерывная процентная ставка (очевидно, что при непре­рывном начислении речь может идти только о сложных процентах) обозначается буквой δ (чи­та­ется «дельта»), часто этот показатель называют «сила роста». Формула наращения по непре­рывной процентной ставке имеет вид:

, (19)

где e – основание натурального логарифма (≈2,71828...),

e^dn – множитель наращения непрерывных процентов.

Например, чему будет равна через 3 года сумма 250 тыс. рублей, если сегодня положить ее на банковский депозит под 15% годовых, начисляемых непрерывно?

S = 250 * e^(0,15 * 3) = 392,1 тыс. рублей.

Для непрерывных процентов не существует различий между процентной и учетной став­ками – сила роста является универсальным показателем. Однако, наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по за­данному закону (математической функции). В этом случае можно строить очень мощные ими­тационные модели, однако математический аппарат расчета таких моделей достаточно сложен и не рассматривается в настоящем пособии, так же как и начисление процентов по переменной непрерывной процентной ставке.

Непрерывное дисконтирование с использованием постоянной силы роста выполняется по формуле:

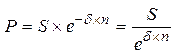, (20)

где 1 / e^dn – дисконтный множитель дисконтирования по силе роста.

Например, в результате осуществления инвестиционного проекта планируется получить через 2 года доход в размере 15 млн. рублей. Чему будет равна приведенная стоимость этих денег в сегодняшних условиях, если сила роста составляет 22% годовых?

P = 15 / e^(0,22 * 2) = 9,66 млн. рублей.

Дата добавления: 2014-01-05