
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементарные финансовые расчеты
|
|
|
|
В предыдущем параграфе были изложены основные принципы применения процентных вычислений в практических финансовых расчетах. Приведенные в этой главе примеры относились к банковской деятельности, так как в этой сфере механизм их действия наиболее нагляден и понятен. Однако, сфера использования финансовых вычислений значительно шире, чем расчет параметров банковских кредитов. Хорошее владение основами финансовой математики позволяет сравнивать между собой эффективность отдельных операций и обосновывать наиболее оптимальные управленческие решения. Для анализа финансовых показателей в настоящее время применятся самые изощренные математические методы. Наличие докторской степени по математике пока не является обязательным требованием для финансового менеджера большинства предприятий, однако знание элементарых свойств финансовых показателей и основных взаимосвязей между ними будет ему необходимы начиная с первого дня практической работы.
Большую помощь финансисту оказывают специальные компьютерные программы, а также финансовые калькуляторы, позволяющие автоматизировать вычисление многих показателей. Широкое распространение получило использование финансовых таблиц для начисления сложных процентов и дисконтирования. В этих таблицах приводятся значения множителей наращения (дисконтных множителей) для заданных n и i. Для нахождения наращенной стоимости достаточно умножить известную первоначальную сумму на табличное значение множителя наращения. Аналогично можно найти приведенную величину будущих денег, умножая их сумму на дисконтный множитель из таблицы. Рассмотим некоторые другие элементарные способы использования результатов финансовых вычислений.
|
|
|
В условиях нестабильной экономики банки и другие кредиторы с целью снижения своего процентного риска могут устанавливать переменные ставки процентов для различных финансовых операций. Например, по ссуде в размере 2 млн. рублей общей продолжительностью 120 дней в течение первых двух месяцев будут начисляться 30% годовых, а начиная с 61 дня ежемесячно простая процентная ставка будет увеличиваться на 5% (обыкновенные проценты). Фактически, ссуда разбивается на несколько составляющих, по каждой из которых установлены свои условия. Необходимо найти наращенные суммы по каждой из составляющих, а затем сложить их. Вспомним, что аналогом процентной ставки в статистике является показатель «темп прироста». При начислении простых процентов следует говорить о базисных темпах прироста, т.к. первоначаьная сумма P остается неизменной. Данная задача в статистических терминах может быть интерпретирована как сложение базисных темпов прироста с последующим умножением на первоначальную сумму займа. Общая формула расчета будет иметь следующий вид:
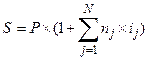 , (1)
, (1)
где N общее число периодов, в течение которых проценты начисляются по неизменной ставке. Подставив в это выражение условия нашего примера, получим:
S = 2 * (1 + (60 / 360 * 0,3) + (30 / 360 * 0,35) + (30 /360 * 0,4)) = 2,225 млн. рублей
Соответственно для сложных процентов, речь пойдет уже не о базисных, а о цепных темпах прироста, которые должны не складываться, а перемножаться:
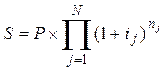 (2)
(2)
Подставив условия примера, получим:
S = 2 * (1 + 0,3)60/360 * (1 + 0,35)30/360 * (1 + 0,4)30/360 = 2,203 млн. рублей
Данную задачу можно решить несколько иным путем – рассчитав сначала средние процентные ставки. Расчет средних процентных ставок (или расчет средних доходностей) вообще очень распространенная в финансах операция. Для ее выполнения полезно опять вспомнить о математико-статистической природе процентных ставок. Так как начисление простых процентов происходит в арифметической прогрессии, средняя простая ставка рассчитывается как средняя арифметическая взвешенная.
|
|
|
 , (3)
, (3)
где N – общее число периодов, в течение которых процентная ставка оставалась неизменной
Сложные проценты растут в геометрической прогрессии, поэтому средняя сложная процентная ставка рассчитывается как средняя геометрическая взвешенная. В качестве весов в обоих случаях используются продолжительности периодов, для которых действовала фиксированная ставка.
 (4)
(4)
Снова используем данные нашего примера. В случае начисления простых процентов получим:
īпр = ((0,3 * 60) + (0,35 * 30) + (0,4 * 30)) / 120 = 0,3375 = 33,75%
S = 2 * (1 + 0,3375 * 120 / 360) = 2,225 млн. рублей
То есть средняя процентная ставка составила 33,75% и начисление процентов по этой ставке за весь срок ссуды дает такой же результат, как и тот, что был получен по формуле (1). Для сложных процентов выражение примет вид:
īсл = ((1 + 0,3)60 * (1 + 0,35)30 * (1 + 0,4)30)1/120 – 1 = 0,33686 = 33,69%
S = 2 * (1 + 0,33686)120/360 = 2,203 млн. рублей
Начисление процентов по средней процентной ставке 33,69% также дает результат, эквивалентный тому, что был получен по формуле (2).
Понимание различий механизмов наращения простых и сложных процентов помогает избегать довольно распространенных ошибок. Например, следует помнить, что такой процесс как инфляция развивается в геометрической, а не в арифметической прогресссии, то есть к нему должны применяться правила начисления сложных, а не простых процентов. Темпы прироста цен в этом случае являются цепными, а не базисными, т.к. в каждом последующем месяце рост цен относится к предыдущему месяцу, а не к началу года или какой-либо иной неизменной базе. Например, если инфляция в январе составила 5%, в феврале 4%, а в марте 9%, то общая инфляция за квартал будет равна не 18% (сумма месячных показателей), а 19,03% (1,05 * 1,04 * 1,09 – 1). Среднемесячный уровень инфляции за этот квартал составит (1,05 * 1,04 * 1,09)1/3 - 1 = 5,98%. С другой стороны, если объявляется, что среднемесячная инфляция за год составила 5,98%, то это не значит, что общая инфляция за год в 12 раз больше (71,76%). На самом деле годовая инфляция в этом случае составит свыше 100,7% (1,059812 - 1).
|
|
|
В предыдущей главе обращалось внимание на сложности, возникающие при попытке понять смысл антисипативного начисления процентов. Рассмотрим ситуацию, в которой необходимо прибегнуть именно к этому способу. Например, коммерсант предлагает вместо оплаты наличными выписать на стоимость закупленных материалов вексель в сумме 500 тыс. рублей со сроком оплаты через 90 дней, который может быть учтен в банке по простой учетной ставкой 25% годовых (коммерческие проценты с точным числом дней ссуды). Для определения суммы, которую понадобится проставить в этом векселе ему необходимо начислить проценты на стоимость товаров, используя антисипативный метод. Сумма векселя составит 533,333 тыс. рублей (500 * 1 / (1 – 90 / 360 * 0,25). Если продавец в этот же день учтет этот вексель в банке (на оговоренных условиях), то получит на руки ровно 500 тыс. рублей (533,333 * (1 – 90 / 360 * 0,25)). Таким образом, начисление антисипативных процентов используется для определения наращенной суммы, которая затем будет дисконтироваться по той же самой ставке, по которой производилось начисление. Такое чисто техническое использование наращения по учетной ставке является преобладающим в практических расчетах.
Наряду с расчетом будущей и современной величины денежных средств часто возникают задачи определения других параметров финансовых операций: их продолжительности и величины процентной или учетной ставок. Например, может возникнуть вопрос: сколько времени понадобится, чтобы данная сумма при заданном уровне процентной ставки удвоилась, или при каком уровне учетной ставки в течение года исходная сумма возрастет в полтора раза? Решение подобных задач сводится к преобразованию соответствующей формулы наращения (дисконтирования) таким образом, чтобы вычислить значение неизвестного параметра. Например, если надо рассчитать продолжительность ссуды по известным первоначальной и будущей суммам, а также уровню простой процентной ставки, то преобразуя формулу начисления простых декурсивных процентов (S = P * (1 + ni)), получим формулу (5) из табл. 2.2.1. (Все формулы и их нумерация приведены в табл. 2.2.1). По такой же формуле будет определяться срок до погашения обязательства при математическом дисконтировании.
|
|
|
Определение срока финансовой операции для антисипативного начисления процентов и банковского учета производится по формуле (6) из табл. 2.2.1. Например, нужно определить через какой период времени произойдет удвоение суммы долга при начислении на нее 20% годовых простых а) при декурсивном методе начисления процентов; б) при использовании антисипативного метода. Временная база в обоих случаях принимается равной 365 дней (точные проценты). Применив формулы (5) и (6), получим:
а) t = (2 – 1) / 0,2 * 365 = 1825 дней (5 лет);
б) t = (1 – 1 / 2) / 0,2 * 365 = 912,5 дней (2,5 года)
Эти же формулы можно применить для определения срока до погашения обязательств при дисконтировании. Например, по векселю номиналом 700 тыс. рублей банк выплатил 520 тыс. рублей, произведя его учет по простой ставке 32% годовых. Чему равен срок до погашения векселя? Применив формулу (6), получим:
t = (1 – 520 / 700) / 0,32 * 360 = 289 дней
Товар, стоимостью 1,5 млн. рублей оплачивается на условиях коммерческого кредита, предоставленного под 15% годовых (простая процентная ставка, временная база 360 дней). Сумма оплаты по истечении срока кредита составила 1 млн. 650 тыс. рублей. Чему равен срок предоставленного кредита? Из формулы (5) следует:
t = (1,65 / 1,5 – 1) / 0,15 * 360 = 240 дней
Таблица 2.2.1
Формулы расчета продолжительности финансовых операций и процентных (учетных) ставок по ним
| Способ начисления процентов | Продолжительность ссуды | Процентная (учетная) ставка |
| 1. Простые декурсивные проценты (t – длительность в днях, K – временная база) |  (5) (5)
| 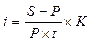 (12) (12)
|
| 2. Простые антисипативные проценты (t – длительность в днях, K – временная база) | 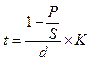 (6) (6)
| 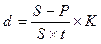 (13) (13)
|
| 3. Сложные декурсивные проценты проценты по эффективной ставке i (n – длительность, лет) | 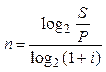 (7) (7)
|  (15) (15)
|
| 4. Сложные декурсивные проценты по номинальной ставке j (n – длительность, лет) | 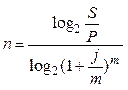 (8) (8)
| 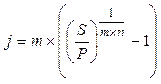 (16) (16)
|
| 5. Дисконтирование по сложной эффективной учетной ставке d (n – длительность, лет) | 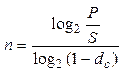 (9) (9)
| 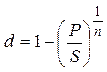 (17) (17)
|
| 6. Дисконтирование по сложной номинальной учетной ставке f (n – длительность, лет) | 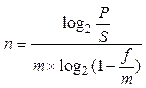 (10) (10)
|  (18) (18)
|
| Непрерывное наращение (дисконтирование) по постоянной силе роста d (n – длительность, лет) | 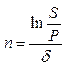 (11) (11)
| 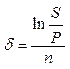 (19) (19)
|
Например, сколько лет должен пролежать на банковском депозите под 20% (сложная процентная ставка i) вклад 100 тыс. рублей, чтобы его сумма составила 250 тыс. рублей? Подставив данные в формулу (7), получим:
n = log2(250 / 100) / log2(1 + 0,2) ≈ 5 лет
Если начисление процентов при этих же условиях будет производиться ежемесячно, то в соответствии с формулой (8):
n = log2(250 / 100) / log2(1 + 0.2 / 12)12 ≈ 4,6 года
Чтобы избежать использования вычислений логарифмов, разработаны упрощенные способы приближенных вычислений срока финансовых операций. Один из них - «правило 70» - позволяет определить период удвоения первоначальной суммы при начислении сложных процентов по приближенной формуле 70% / i. Проверим его на нашем примере, заменив значение наращенной суммы 250 тыс. рублей на 200 тыс. рублей. По «правилу 70» эта сумма должна быть накоплена через 3,5 года (0,7 / 0,2). Подставив соответствующие значения в формулу (7) получим 3,8 года.
Еще одним важнейшим параметром любой финансовой операции является процентная (учетная) ставка. Кроме технической функции, выполняемой этим показателем в ходе расчетов, он используется для оценки доходности – одного из фундаментальных понятий финансового менеджмента. Часто можно услышать (или прочитать) выражения, подобные следующим: “на этой сделке я заработал 50%” или “менеджеры нашего фонда обеспечат годовую доходность по Вашим вкладам не ниже 100% ” и т.п. Следует сразу оговориться, что сами по себе эти выражения вполне корректны, однако объем содержащейся в них полезной информации значительно меньше, чем может показаться на первый взгляд. Из содержания предыдущей главы можно сделать вывод, что любое упоминание о процентных ставках требует массу оговорок и уточнений. Попытаемся понять смысл первого выражения. Во-первых следует уточнить, к какому промежутку времени относится полученный доход – месяцу, году или длительности самой сделки. В последнем случае необходимо знать, чему равна эта длительность. Так как ничего не известно ни о сумме ни о длительности сделки, то ее результат “50% дохода” невозможно сравнить с доходностью какой-то другой операции, чтобы сделать вывод об уровне ее эффективности. Если в ответ на это выражение кто-нибудь заявит: “А я имею 25% годовых по своему банковскому депозиту”, то определить, который же из этих двух инвесторов оказался более удачливым, будет практически невозможно.
Сталкиваясь с упоминанием о процентных ставках, финансист должен выяснить о каких процентах – простых или сложных, дискретных или непрерывных, – идет речь. Далее необходимо точно определиться с временной базой – рассчитываются ли годовые проценты или какие-то еще, если проценты годовые, то возникает вопрос, каким образом определяется длительность операции и продолжительность года. В случае начисления сложных процентов должно быть оговорено количество начислений процентов в течение года. В результате может оказаться, что методика определения доходности, используемая одним из контрагентов, не совпадает с той, что “принята на вооружение” другой стороной. Однако в этом уже не будет никакой трагедии, так как, зная особенности обеих этих методик, финансисты достаточно быстро приведут результаты своих расчетов в сопоставимый вид. То есть, своевременно задавая необходимые вопросы, финансист тем самым предотвращает возможные неприятные последствия использования несогласованных терминов. Вряд ли в обозримом будущем удастся заставить всех рассчитывать доходность по какой-либо единой методике, поэтому задача финансиста состоит не в том, чтобы вынудить своего контрагента применять единственноый “правильный” способ, а в том, чтобы как можно скорее разобраться самому, что именно понимает под термином “доходность” его собеседник, и после этого решить, каким образом можно унифицировать расчеты. Вопросы определения доходности заслуживают отдельного разговора, поэтому здесь будут рассмотрены наиболее общие моменты расчета уровня процентных ставок в отдельных финансовых операциях и нахождения эквивалентных им значений.
Вначале рассмотрим способы расчета величины процентных (учетных) ставок, когда заданы другие параметры финансовой операции. Преобразовав формулы декурсивного и антисипативного наращения простых процентов, получим выражения (12) и (13) в табл. 2.2.1). Например, чему будет равна простая процентная ставка по ссуде, выданной на 90 дней в размере 350 тыс. рублей, и возвращенной по истечении срока в сумме 375 тыс. рублей (временная база 360 дней)? Подставив эти данные в формулу (12), получим:
i = (375 – 350) / (350 * 90) * 360 ≈ 28,6%
Вексель номиналом 1 млн. рублей учтен в банке за 60 дней до его погашения в сумме 900 тыс. рублей. По какой простой учетной ставке было произведено его дисконтирование? Используем для расчетов формулу (13):
d = (1 – 0,9) / (1 * 60) * 360 = 60%
Очевидно, что даная методика может (и должна) использоваться при анализе любых финансовых операциях, а не только в процессе банковского кредитования. Например, иностранная валюта в объеме 1000 единиц, купленная по курсу 20 руб. за 1 единицу, через месяц была продана по курсу 20 руб. 50 коп. Определить доходность этой операции по годовой простой процентной ставке (коммерческие проценты). Из формулы (12) получаем:
i = (20500 – 20000) / (20000 * 30) * 360 = 30%
Аналогичный подход к расчету доходности используется и на фондовых рынках. Например, Центральным Банком России была рекомендована следующая формула расчета доходности ГКО:
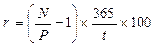 , (14)
, (14)
где N – номинал облигации;
P – цена ее приобретения;
t – срок до погашения.
По сути дела она повторяет формулу (12) применительно к точным процентам (временная база 365 дней). Например, облигация номиналом 10 тыс. рублей была приобретена за 8,2 тыс. рублей за 40 дней до погашения. Ее годовая доходность, рассчитанная как простая процентная ставка, составит:
r = (10 / 8,2 – 1) * 365 / 40 * 100 ≈ 200,3%
Точно такой же результат можно получить, применив формулу (12).
Не следует отождествлять процентную ставку, указываемую в кредитном договоре, с доходностью операции, рассчитанной в процентах. В первом случае процентная ставка является реальным параметром финансовой операции, однозначно определяющим величину платежа, который должен последовать в случае исполнения договора. Доходность же – это производная величина, не определяющая, а определяемая теми денежными потоками, которые порождает кредитный договор (ценная бумага или другой финансовый инструмент). В первой главе данного пособия подчеркивался абстрактный характер понятия “прибыль предприятия”. То же самое можно сказать о доходности – в явной форме она не присутствует в ходе осуществления финансовой операции. Рассчитывая доходность финансовой операции, инвестор получает субъективную оценку ее величины, зависящую от целого ряда предпосылок, таких как способ начисления процентов, выбор временной базы и т.п. Эти предпосылки не являются объективными и неизбежными – при всем уважении к Центральному банку инвестор может определить доходность купленной им ГКО по ставке сложных, а не простых процентов, не нарушив при этом ни физических ни юридических законов (и поступив совершенно правильно с позиции финансовой теории).
Рекомендация вычислять доходность по методике наращения простых процентов используется на данном рынке как соглашение его участников (точно такое же как соглашение о подсчете точной временной базы). Выполнение условий этого соглашения гарантирует участникам рынка сопоставимость результатов их расчетов, т.е. помогает избежать путаницы, но не более этого. Степень соответствия того либо иного метода расчета доходности идеалу в данном контексте не имеет значения – это предмет научных дискуссий. Используя неправильную или несовершенную методику расчета доходности, инвестор имеет все шансы достаточно быстро разориться, точно так же как и предприятие, завышающее прибыль, вследствие неправильного калькулирования издержек. Но конечной причиной банкротства станет отсутствие у него денег для покрытия обязательств, до этого момента ни один кредитор не сможет вчинить иск о банкротстве только на основании несогласия с методикой подсчета доходности, которой пользуется его должник.
Для финансового менеджмента сложные проценты имеют неизмеримо большую ценность, чем простые. Очевидно, что при использовании методики расчета простых процентов значение доходности искажается уже из-за того, что данная методика не учитывает возможности реинвестирования полученных доходов. Пэтому при прочих равных условиях безусловно предпочтительным является расчет доходности как ставки сложных процентов. Рассмотрим методику определения величины этой ставки, когда известны другие параметры финансовой операции. В результате преобразования исходных выражений наращения (дисконтирования) по сложным процентам, получим (см. (15) – (19) в табл. 3.2.1).
В качестве иллюстрации рассчитаем доходность облигации из предыдущего примера как ставку сложного процента (наращение 1 раз в году):
i = (10 / 8,2)365/40 – 1 ≈ 511,6%
Этот результат более чем в 2,5 раза превышает доходность, рассчитанную как ставку простых процентов. Означает ли это, что инвестор, использующий для расчета доходности сложные проценты, в два с половиной раза богаче того, кто купив в один день с ним точно такую же облигацию, применяет для вычислений простые проценты? Тогда последнему следует срочно разучивать новую формулу и точно так же богатеть.
Однако, в случае сложных процентов не все так однозначно. Если рассчитывать доходность как сложную номинальную ставку (16), то ее уровень резко снизится, при m = 12 получим:
j = 12 * ((10 / 8,2)1/(12*40/365)) – 1 ≈ 195,5%
При расчете доходности как силы роста – непрерывные проценты (19) – ее уровень будет более точно соответствовать тому, что был рассчитан с помощью простой процентной ставки:
d = ln (10 / 8,2) / (40 / 365) ≈ 203,6%
Чтобы не запутаться в обилии методов расчета процентных ставок не обязательно зазубривать каждую формулу. Достаточно четко представлять, каким образом она получена. Кроме этого, следует помнить, что любому значению данной ставки может быть поставлено в соответствие эквивалентное значение какой-либо другой процентной или учетной ставки. В предыдущей главе был приведен подобный пример эквивалентности между простыми процентной и учетной ставками (5). Эквивалентными называются ставки, наращение или дисконтирование по которым приводит к одному и тому же финансовому результату. Например, в условиях последнего примера эквивалентными являются простая процентная ставка 200,3% и сложная процентная ставка 511,6%, т.к. начисление любой из них позволяет нарастить первоначальную сумму 8,2 тыс. рублей до 10 тыс. рублей за 40 дней. Приравнивая между собой множители наращения (дисконтирования), можно получить несложные формулы эквивалентности различных ставок. Для удобства эти формулы представлены в табличной форме. В заголовки граф табл. 3.2.2 помещены простые процентная (i) и учетная (d) ставки. В заголовках строк этой таблицы указаны все рассмотренные в данном пособии ставки. На пересечении граф и столбцов приводятся формулы эквивалентности соответствующих ставок. В таблицу не включены уравнения эквивалентности простых процентных и сложных учетных ставок, вследствие маловероятности возникновения необходимости в таком сопоставлении.
Знание уравнений эквивалентности позволяет без труда переходить от одного измерения доходности к другому. Например, доходность облигаций по простой процентной ставке составила за полгода 60%. По формуле (21) найдем, что в пересчете на сложные проценты это составляет 69%. Доходность векселя, дисконтированного по простой учетной ставке 50% за 3 месяца до срока погашения, в пересчете на простую процентную ставку составит 57,14% (34), если же по процентной ставке принята точная временная база (365 дней), то применив формулу (36), получим i = 57,94%).
Таблица 2.2.2
Эквивалентность простых ставок
| Простая процентная ставка (iпр) | Простая учетная ставка (dпр) | |
| Сложная процентная ставка (iсл) | 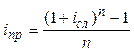 (20) (20)
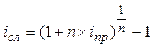 (21) (21)
|  (22) (22)
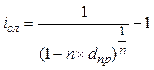 (23) (23)
|
| Сложная номинальная процентная ставка (j) |  (24) (24)
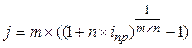 (25) (25)
| 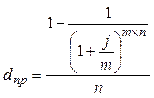 (26) (26)
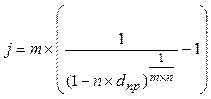 (27) (27)
|
| Сила роста (d) | 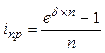 (28) (28)
 (29) (29)
|  (30) (30) 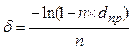 (31) (31)
|
| Простая учетная ставка (dпр) n = t / K |  (32) (32)
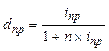 (33) (33)
| – |
| Простая учетная ставка (dпр) ki = kd = 360 | 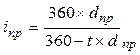 (34) (34)
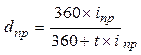 (35) (35)
| – |
| Простая учетная ставка (dпр) ki = 365 kd = 360 |  (36) (36)
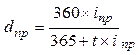 (37) (37)
| – |
Например, предприятие может столкнуться с необходимостью выбора между получением кредита на 5 месяцев под сложную номинальную ставку 24% (начисление процентов поквартальное) и учетом в банке векселя на эту же сумму и с таким же сроком погашения. Небходимо определить простую учетную ставку, которая сделает учет векселя равновыгодной операцией по отношению к получению ссуды. По формуле (26) получим d = 22,21%.
Кроме формул, приведенных в табл. 3.2.2 и 3.2.3, следует отметить еще одно полезное соотношение. Между силой роста и дисконтным множителем декурсивных процентов существунт следующая связь:
 (38)
(38)
По мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения непрерывных процентов будет расширяться, так как при этом становится возможным использовать более мощный математический аппарат. Особенно наглядно это проявляется в случае непрерывных процентных ставок. В обыденной практике финансистов данный способ пока еще не занял должного места, что в какой-то мере объясняется его непривычностью, может быть чересчур «отвлеченным» характером. Однако трезвый анализ показывает, что предположение о непрерывности реинвестирования начисленных процентов не такое уж абстрактное и нереальное. В самом деле, как для простых, так и для сложных процентов факт непрерывности их начисления ни у кого не вызывает сомнений (годовая ставка 36% означает 3% в месяц, 0,1% в день и т.д., то есть можно начислять проценты хоть за доли секунды). Но точно такой же аксиомой для финансов является признание возможности мгновенного реинвестирования любых полученных сумм. Что же мешает совместить два этих предположения? В теории сумма начисленных процентов может (и должна) реинвестироваться сразу по мере ее начисления, т.е. непрерывно. В данном утверждении ничуть не меньше логики, чем в предположении, что реинвестирование должно производиться дискретно. Почему реинвестирование 1 раз в год считается более «естественным» чем 12 или 6 раз? Почему эта периодичность привязывается к календарным периодам (год, квартал, месяц), почему нельзя реинвестировать начисленные сложные проценты, скажем 39 раз в год или 666 раз за период между двумя полнолуниями? На все эти вопросы ответ, скорее всего, будет один – так сложилось, так привычно, так удобнее. Но выше уже было отмечено, что практический расчет величины реальных денежных потоков (например, дивидендных или купонных выплат) и определение доходности финансовых операций это далеко не одно и то же. Если привычнее и удобнее выплачивать купон по облигации 2 раза в год, то так и следует поступать. Но, определять доходность этой операции более логично по ставке непрерывных процентов.
Таблица 2.2.3
Эквивалентность сложных процентных ставок
| Сложная процентная ставка (iсл) | Сложная учетная ставка (dсл) | |
| Сложная номинальная процентная ставка (j) | 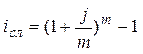 (39) (39)
 (40) (40)
| 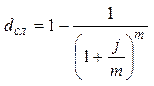 (41) (41)
 (42) (42)
|
| Сила роста (d) |  (43) (43)
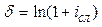 (44) (44)
| Сложная номинальная процентная ставка (j) |
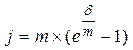 (45) (45)
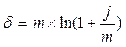 (46) (46)
| ||
| Сложная учетная ставка (dсл) | 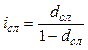 (47) (47)
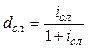 (48) (48)
| – |
Например, по вкладу в размере 10 тыс. рублей начисляется 25 простых процентов в год. В конце 1 года вклад возрастет до 12500 рублей. Доходность, измеренная как по простой (формула 12), так и сложной (15) процентной ставке i, составит 25% годовых. Однако, измеряя доходность по номинальной ставке j (16) при m = 2, получим лишь 23,61%, т.к. в этом случае будет учтена потерянная вкладчиком возможность реинвестирования процентов хотя бы 2 раза в год. Если же измерить доходность по силе роста (19), то она окажется еще ниже – всего 22,31%, т.к. теоретически он мог реинвестировать начисленные проценты не 2 раза в год, а непрерывно.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 285; Нарушение авторских прав?; Мы поможем в написании вашей работы!