Та особливості розрахунку відкритих зубчастих передач

ПРОЕКТНИЙ РОЗРАХУНОК ЦИЛІНДРИЧНИХ ЗУБЧАСТИХ ПЕРЕДАЧ

Проектний розрахунок. Добуті вище розрахункові залежності σ_Н; σ_{H max}; σ_F; та σ_{F max} використовують для перевірних розрахунків на міцність зубчастих передач із відомими розмірами та навантаженням.

Проектний розрахунок має бути тільки для попереднього визна­чення орієнтовних розмірів передачі і не може замінити виконання перевірних розрахунків, які є основними.

Габаритні розміри зубчастої передачі ви­значаються умовою стійкості активних поверхонь зубців проти втом­ного викришування. Тому розрахункову залежність для визначен­ня основного розмірного параметра передачі, який визначає її габаритні розміри, дістанемо з умови (23.26). Таким розмірним параметром для циліндричних зубчастих передач можна вважати міжосьову відстань a_W.

Вихідними даними для проектного розрахунку передачі є такі: розрахункове тривало діюче навантаження T_1H передаточне число передачі u; параметр ψ_ba = b/a_W або ψ_bd = b/d₁ рекомендації для вибору яких наведені у 23.1; вид передачі – прямозуба чи косозуба (шевронна); типовий режим навантаження передачі та строк її служби; матеріали зубчастих коліс, їх термообробка, твердість ак­тивних поверхонь зубців; за цими даними попередньо розраховують допустиме контактне напруження [σ]_н.

Вивід формули для визначення мінімально допустимої міжосьової відстані передачі a_W подамо у певній послідовності. У формулі (23.26) виконаємо заміну дістанемо

σ_н = Z_M · Z_H · Z_ε ·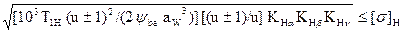

Із записаного співвідношення визначимо a_w:

a_W ≥ (u ± 1) · .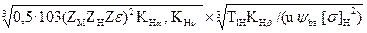

Якщо додатково позначити

К_a = ,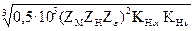

то можна дати остаточний запис формули для визначення мінімальної міжосьової відстані передачі у такому вигляді:

a_{w min} = К_а · (u ± 1) · 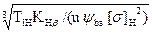. (23.32)

У формулі (23.32) обертовий момент Т_ІH слід брати у ньютон–метрах (Нм), допустиме напруження [σ]_н – у мегапаскалях (МПа), а міжосьову відстань a_wmin – у міліметрах (мм)

Допоміжний коефіцієнт К_а у формулі (23.32) враховує параметри передачі, які попередньо можуть бути вибрані цілком однозначно, і параметри, які не можуть бути завчасно і точно визначені (Z_ε, К_Hα, K_Hv). Тому коефіцієнту К_а надається деяка наближена оцінка і ре­комендується брати: К_а = 495 МПа¹/³, К_а = 415 МПа¹/³ – для прямозубих передач із сталевими та чавунними зубчастими колесами відповідно;

К_а =430 МПа¹/³, К_а = 360 МПа¹/³ – для косозубих (шевронних) передач із сталевими та чавунними колесами відповідно.

Коефіцієнт К_Нβ що враховує нерівномірність розподілу наванта­ження по ширині зубчастих вінців, вибирають залежно від пара­метра ψ_bd за графіками на рис. 23.8.

Формула (23.32) дає змогу оцінити ступінь впливу окремих параме­трів передачі u, ψ_bd, [σ]_н на її габаритні розміри.

Обчислена за формулою (23.32) міжосьова відстань a_wmin дає можливість визначити модуль зубців та розміри вінців зубчастих ко­ліс. Потрібний модуль може бути визна­чений за формулою

m'_n = 2a_{w min} · cos β / (z₁+z₂). (23.33)

Значення m_n округляють до найближчого стандартного значення m_n згідно з ГОСТ 9563–60.

Із співвідношення (23.33) видно, що при одній і тій же міжосьовій відстані передачі можна дістати різні модулі зубців при зміні чисел зубців шестірні Z₁ та колеса z₂. При великих значеннях z₁ і відповід­но z₂ = u∙z₁ маємо зубчасті колеса із малим модулем, а при малих значеннях z₁ та z₂ – із великим модулем.

Маломодульні колеса з великим числом зубців мають переваги за умовою підвищеної плавності роботи (збільшується ε_α) та за економічними міркуваннями. При малих значеннях т зменшуються втрати на тертя у зачепленні (зменшується ковзання), скорочуються витрати матеріалу (зменшується d_a), економиться час при нарізу­ванні зубців (зменшується кількість матеріалу, який зрізається). Однак при малих модулях зростають вимоги до точності та жорсткос­ті передачі, суттєво зменшується міцність зубців на згин [див. фор­мулу (23.30)].

Великомодульні колеса з великими розмірами зубців не так чут­ливі до спрацювання, можуть працювати тривалий час після початку втомного викришу–вання активних поверхонь, менш чутливі до пере­вантажень та неоднорідності матеріалу, але плавність роботи пере­дачі з такими колесами значно падає.

Виходячи з наведених міркувань, для силових зубчастих передач рекоме–ндують брати m ≥ 1,5 мм.

Здебільшого число зубців шестірні z₁ > z_min, де z_min – мінімаль­не число зубців за умови непідрізання ніжок. Для некоригованих прямозубих коліс z_min = 17, а для коліс із кутовою корекцією міні­мальне число зубців може бути 10. У косозубих та шевронних коле­сах мінімальне число зубців залежить від кута нахилу лінії зуб­ців, наприклад, якщо β = 21...24°, то z_min= 14, а якщо β = 28... 31°, то z_min = 12.

З метою зменшення шуму у швидкохідних передачах рекоменду­ють брати z₁ ≥ 25.

Щоб остаточно впевнитись у правильності вибору чисел зубців z₁, z₂ і модуля m, треба перевірити міцність зубців на втому при зги­ні. У разі отримання незадовільного результату зменшують у допус­тимих межах z₁ і відповідно z₂ і тим самим збільшують модуль m.

Слід зазначити, що при перевірці міцності зубців на втому при згині можна дістати σ_F значно менше від [σ]_F. Це не є суперечливим або недопустимим результатом, оскільки габаритні розміри передачі за несучою здатністю обмежуються контактною міцністю активних поверхонь зубців, а не їхньою міцністю на згин.

Якщо розрахункове напруження σ_F перевищує допустиме [σ]_F, то, крім збільшення модуля зубців, можна застосовувати зубчасті колеса із зміщенням. У таких випадках вирішальне значення має не контактна міцність, а міцність зубців на згин. На практиці такі випадки можуть бути у зубчастих колесах із твердістю активних по­верхонь зубців Н > 50...60 HRC у реверсивних передач.

Особливості розрахунку відкритих зубчастих передач. У відкритих передачах використовують прямозубі циліндричні або конічні коле­са. Такі передачі працюють при колових швидкостях зубчастих коліс не більш як 2 м/с. Зубці відкритих передач припрацьо­вуються при довільних твердостях їхніх робочих по­верхонь. Здебільшого колеса виготовляють із норма­лізованих або поліпшених сталей. У процесі роботи передачі зубці інтенсивно спрацьовуються, що визна­чає особливості їхнього розрахунку.

Відкриті передачі проектують з вузькими колесами (коефіцієнт ширини вінця ψ_ba = 0,10...0,15). Розміри передачі визначають із розрахунку на контактну втому з подальшою перевіркою на згин (за анало­гією закритих передач). Міжосьову відстань переда­чі визначають за формулою (23.32), При цьому коефі­цієнти, що враховують розподіл навантаження по ширині вінця коліс, беруть К_Нβ = К_НF =1.

Спрацювання зубців у відкритих передачах допускається до 25 % початкової їхньої товщини по ділильному колу. Міцність зубців на згин при цьому зменшується приблизно у 2 рази. Тому треба так підібрати модуль зубців, щоб розрахункове напруження згину σ_F за формулою (23.30) було в 2 рази менше від попередньо обчисленого допустимого напруження [σ]_F.

Дата добавления: 2014-01-05