Розрахунок зубців на втому і міцність при згині

Розрахунок зубців на втому при згині. При розрахунках на згин зубець розглядають як консольну балку. Розрахункове навантажен­ня прикладається до вершини зубця, тобто вибирають найнебезпечніший випадок навантаження зубця з точки зору виникнення макси­мального напруження згину у його основі.

На рис. 23.9 зображена розрахункова схема зубця. Зубець зав­довжки 1 мм навантажений розрахунковою силою q_F, яка визнача­ється за виразом (23.23).

Перенесемо точку прикладання сили q_F на вісь симетрії зубця і розкладемо цю силу на дві взаємно перпендикулярні складові: q_Ft = q_F cos α'; q_Fr = q_F sin α',

де α' – кут, що визначає положення век­тора навантаження q_F щодо осі зубця.

Рисунок 23.9 До визначення напружень згину в зубці зубчастого колеса

У небезпечному перерізі, який розміщений в основі зубця у зоні найбільшої концентрації напружень, навантаження q_Ft спричинює напруження згину σ_зг, а наван­таження q_Fr– напруження стиску σ_ст (див. епюри на рис. 23.9):

σ_зг = q_Ft · l/W₀ = 6 · q_F · l · cos α'/α²; σ_ст = q_Fr /A = q_F · sin α'/α.

На рис. 23.9 показана також епюра сумарних напружень σ_f у небезпечному перерізі зубця. Оскільки втомні тріщини і руйнування починаються на розтягнуто­му боці зубців (тобто з боку робочого про­філю), міцність зубців розраховують саме з цього боку за умовою, що

σ_f = Y_β· (σ_зг – σ_ст) · α_k ≤ [σ]_F, (23.29)

де Y_β – коефіцієнт, що враховує зменшення напружень при нахиле­ному розміщенні зубців у косозубих передачах; α_k – теоретичний коефіцієнт концентрації напружень.

Розміри l і a (див. рис. 23.9) пропорційні модулю зубців т_п: l = λ₁ · т_п : а = λ · ₂т_п

(λ₁ і λ₂ – коефіцієнти пропорційності). Якщо це взяти до уваги та підставити значення σ_зг та σ_ст в умову (23.29), то дістанемо

σ_f = Y_β · α_k · [6q_F · λ₁ · m_n · cos α'/(λ²₂ · m²_n) – q_F · sin α'/(λ₂ · m_n)] =

= (q_F ·Y_β · α_k/m_n) (6 · λ₁ · cos α'/ λ²₂ – sin α'/ λ₂) ≤ [σ]_F.

Врахуємо залежність (23.23) для визначення розрахунково­го навантаження на зубці.

Остаточна формула для розрахунку зубців на втому при згині набуде вигляду

σ_f = Y_F · Y_ε · Y_β · W_Ft/m_n < [σ] _f. (23.30)

Тут W_Ft – питома розрахункова колова сила, яка визначається ва формулою (23.21):

W_Ft= (F_Ft/b) · К_Fα, К_Fβ, K_Fv.

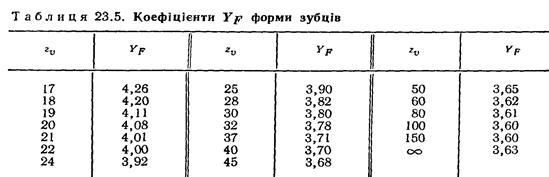
В умові міцності (23.30) маємо такі коефіцієнти: Y_F – коефіці­єнт форми зубців (залежить від розмірів l, а, α' та форми перехідної кривої зубця, яка впливає на α_k); Y_F визначають за відповідними графіками залежно від еквівалентного числа зубців Z_V шестірні та колеса [див. формулу (23.9)] з урахуванням коефіцієнтів зміщен­ня х; для некоригованих коліс (х = 0) зовнішнього зачеплення значення Y_F наведені у табл. 23.5, а для коліс внутрішнього за­чеплення наближено можна брати

Y_F = 4z /(z + 20);

Y_ε – коефіцієнт перекриття зубців, у розрахунках прямозубих та косозубих (шевронних) передач можна наближено брати Y_ε = 1; Y_β – коефіцієнт нахилу зубців, для прямозубих передач Y_β = 1, а для косозубих та шевронних Y_β = 1– β/140°.

Перевірку міцності зубців на втому при згині виконують для зуб­ців шестірні і колеса, оскільки Y_F1 та Y_F2 різні при z₁ ≠ z₂.

Із співвідношення (23.30) видно, що за інших рівних умов напру­ження згину в зубцях тим більші, чим менший модуль зубців т_п. Міцність зубців на згин для передачі з відомою міжосьовою відстанню можна підвищити, збільшуючи модуль та зменшуючи відповідно числа зубців шестірні та колеса.

Розрахунок зубців на міцність при згині максимальним наванта­женням виконують для того, щоб запобігти появі залишкової дефор­мації або крихкої поломки зубців. Цей розрахунок ведуть за най­більшим короткочасним навантаженням T_{1 max} для зубців того зуб­частого колеса (шестірні або колеса), для якого напруження згину σ_F більше.

Щоб забезпечити потрібну міцність зубців, треба виконувати таку умову:

σ_{н max} = σ _F · (T_{1 max} / T_{1 F}) ≤ [σ] _{F max,} (23.31)

де σ _{F max} – максимальне розрахункове напруження згину; σ _F – розрахункове напруження згину, що спричинюється дією наванта­ження T_1F; [σ] _{F max} – допустиме граничне на­пруження згину.

Дата добавления: 2014-01-05