Радіуси кривини профілів зубців та приведена їхня кривина

У розрахунках зубців зубчастих коліс на контактну втому використо­вують зведену кривину профілів зубців у їхньому нормальному пере­різі, коли точка контакту профілів знаходиться у полюсі зачеплення.

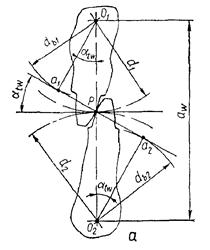
Для прямозубої передачі (рис. 23.4, а) радіуси кривини профілів зубців у полюсі зачеплення визначають за такими формулами:

ρ₁ = a₁· P = 0,5·d₁· sin α _{t ω} ;

ρ₂ = a₂· P = 0,5·d₂· sin α _{t ω} , (23.10)

де α _{t ω} – кут зачеплення, який у некоригованих зубчастих колесах дорівнює

ділильному куту профілю зубців α _{t ω} = α = 20°).

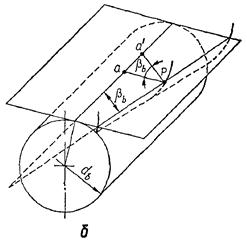
У косозубому зубчастому колесі радіус кривини профілю у нор­мальному перерізі зубця (рис. 23.4, б)

ρ_n = a^' · P = (a · P) / cos β _b = ρ / cos β _b

Відповідно для косозубих шестірні та колеса з урахуванням за­лежностей (23.10) маємо для нормального перерізу зубців: ρ_n1 = 0,5d₁ · sin α_n/cos β _b; ρ_n2= 0,5d₂ · sin α_n/cos β _b, (23.11)

де β _b – кут нахилу лінії зубців на основному циліндрі діаметром d_b.

У точці контакту зубців зведена кривина їхніх профілів

1/ρ_зв = 1/ρ_n1 ± 1/ρ_n2 = 2cos β _b /d₁sin α_n ± 2 cos β _b / d₂ sin α_n = 2 cos β _b / sin α_n (1/d₁ ± 1/d₂)

Якщо d₂ = ud₁, то остаточно запишемо 1/ρ_зв = [2 cos β _b · (d₁ · sin α_n)] · (u ± 1)/ u. (23.12) Тут знак плюс – для передач зовнішнього зачеплення; знак мі­нус – для передач внутрішнього зачеплення.

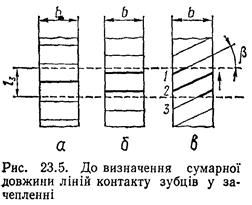
Сумарна довжина ліній контакту зубців у зачепленні. Сумарна дов­жина контактних ліній l_Σ зубців, що одночасно знаходяться у зачеп­ленні, залежить від значення коефіцієнтів торцевого ε_α та осьового ε_β перекриття. В прямозубих передачах l_Σ різко змінюється при переспряженні зубців (рис. 23.5,а,б). Здебільшого 1 < ε_α < 2 і су­марна довжина контактних ліній у період однопарного зачеплення (рис. 23.5, а) буде l_Σ = b, а у період двопарного зачеплення l_Σ = 2 b (рис. 23.5, б).

У косозубих передачах (рис. 23.5, в) сумарна довжина контакту l_Σ = b · ε_α / cosβ (23.13)

Якщо ε_α або ε_β – ціле число, то l_Σ у косозубій передачі не змі­нюється, оскільки зменшення довжини контакту зубця 1 (рис. 23.5, в) відповідає такому ж збільшенню довжини контакту зубця 3 при не­змінній довжині контакту зубця 2.

У загальному випадку ε_α і ε_β не цілі числа і l_Σ коливається у деяких межах. Тому рекомендується сумарну довжину ліній контакту зубців визначати за формулою l_Σ =К_ε · b · ε_α / cos β, (23.14)

де К_ε – коефіцієнт, що враховує коливання сумарної довжини ліній контакту зубців.

Для розповсюджених на практиці зачеплень величина К_ε змінюється в межах 0,9–1,0. У середньому можна брати К_ε = 0,95.

Найвигіднішим для роботи зубчастої передачі є випадок l_Σ = const. Цього можна досягнути відповідним вибором β та ширини зубчастого вінця b так, щоб коефіцієнт осьового перекриття ε_β був цілим числом [див. формулу (23.7)].

Дата добавления: 2014-01-05